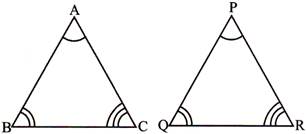
 e.g., If in \[\Delta \,ABC\]and \[\Delta \,PQR\]
\[\angle A=\angle P,\angle B=\angle Q,\angle C=\angle R\]
and \[\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR},\] then, \[\Delta \text{ }ABC\sim \Delta \,PQR;\] where symbol \[\sim \] is read as ‘is similar to’.
more...
e.g., If in \[\Delta \,ABC\]and \[\Delta \,PQR\]
\[\angle A=\angle P,\angle B=\angle Q,\angle C=\angle R\]
and \[\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR},\] then, \[\Delta \text{ }ABC\sim \Delta \,PQR;\] where symbol \[\sim \] is read as ‘is similar to’.
more...
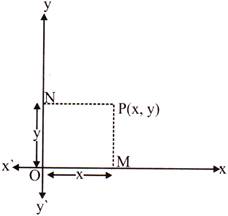 Draw PM and PN perpendiculars on OX and OY respectively. OM is called the x co – ordinate or abscissa of the point P. ON is called the y co – ordinate or the ordinate of the point P.
The abscissa and ordinate of a point are known as co – ordinates of the point P.
If OM = x, ON = y, then the more...
Draw PM and PN perpendiculars on OX and OY respectively. OM is called the x co – ordinate or abscissa of the point P. ON is called the y co – ordinate or the ordinate of the point P.
The abscissa and ordinate of a point are known as co – ordinates of the point P.
If OM = x, ON = y, then the more...
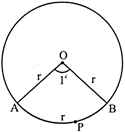 Relation between the Units
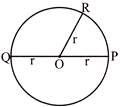
Look at the circle in the above figure and note that,
\[360{}^\circ =2{{\pi }^{c}}\Rightarrow 90{}^\circ =\frac{{{\pi }^{c}}}{2}\] and \[45{}^\circ =\frac{{{\pi }^{c}}}{4}\]; Or, simply, \[90{}^\circ =\frac{\pi }{2},45{}^\circ =\frac{\pi }{4}\]
For convenience, the above relation can be written as, \[\frac{D}{90}=\frac{R}{\frac{\pi }{2}}\], where, D denotes degrees, and R radians.
Remember
Relation between the Units
Look at the circle in the above figure and note that,
\[360{}^\circ =2{{\pi }^{c}}\Rightarrow 90{}^\circ =\frac{{{\pi }^{c}}}{2}\] and \[45{}^\circ =\frac{{{\pi }^{c}}}{4}\]; Or, simply, \[90{}^\circ =\frac{\pi }{2},45{}^\circ =\frac{\pi }{4}\]
For convenience, the above relation can be written as, \[\frac{D}{90}=\frac{R}{\frac{\pi }{2}}\], where, D denotes degrees, and R radians.
Remember
You need to login to perform this action.
You will be redirected in
3 sec
