Straight Lines
The locus of the points taken in one direction is called straight lines. The slope of the straight lines is the angle which the line make with the positive direction of x- axis. It is denoted by 'm' or' tan \[\theta \]'or' \[\frac{dy}{dx}'\]
Thus the most general form of the equation of the straight line having slope 'm' and y-intercept 'c' is given by:
Y = mx + c
Equation of the Line Passing Through One Point
Let \[P({{X}_{1}},{{Y}_{1}})\] be the given point having slope 'm', then the equation of the line is given by \[(Y-{{Y}_{1}})=m(X0-{{X}_{1}})\]
Equation of Line Passing Through Two Given Points
Let \[P({{X}_{1}},{{Y}_{2}})\,and\,Q({{X}_{2}},{{Y}_{2}})\] be more...
Distance Between two Points
Let us consider the two points \[A({{x}_{1}}{{y}_{1}}),\And B({{x}_{2}},{{y}_{2}}),\] in a two dimensional plane, then the distance between the two points is given by \[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]. If it is a three dimensional plane containing the points \[A({{x}_{1}},{{y}_{1}},{{z}_{1}})\And B({{x}_{2}},{{y}_{2}},{{z}_{2}},{{z}_{2}}),\] then the distance between the points is given by: \[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}\]
Proof of Finding Distance Between Two Points
Let \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\] be the given points.
Draw AL \[\bot \] OX and AN \[\bot \] BM
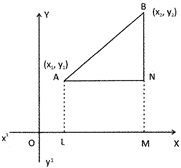
Now, from Figure
\[OL={{X}_{1}},OM={{X}_{2}},AL={{Y}_{1}}\And BM={{Y}_{2}}\].
\[\therefore \,\,\,AN=LM=(OM-OL)={{X}_{2}}-{{X}_{1}}\]
BN = (BM - NM) = (BM - AL) \[={{Y}_{2}}-{{Y}_{1}}\,\,[\therefore \,NM=AL]\]
From right \[\Delta ANB\], By Pythagorean" theorem, we have \[A{{B}^{2}}=(A{{N}^{2}}+B{{M}^{2}})\]
\[\Rightarrow \,\,{{(AB)}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}\]
\[\Rightarrow \,\,(AB)=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}}\]
Hence, the distance between the points \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\] given by:
\[(AB)=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}}\]
Section Formula
Let us consider more...
Introduction
In this chapter we will discuss about the two as well as three dimensional geometry. We will discuss about the position of the points and locate the point in the plane or on the surface. The three mutually perpendicular lines in the plane is called coordinate axes of the plane. The three numbers in a plane which represents the positions of the point is called coordinate of the point with reference of to the three coordinate planes. There are eight planes in a three dimensional axes called octants. The sign of the various coordinates in the various octants are given below in the table:
| Coordinate | more...
 Introduction
Circle is defined as the locus of a point which is at a constant distance from a fixed point. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle.
Tangent to a circle
A tangent to a circle is a line which intersects the circle at exactly one point. The point where the tangent intersects the circle is known as the point of contact.
 Properties of tangent to a circle
Following are some properties of tangent to a circle:
In this chapter we will discuss about the similarity of triangles. Two figures having the same shape and not necessarily the same size are called the similar figures. Two polygons of the same number of sides are similar if their corresponding angles are equal and their corresponding sides are in the same ratio.
 Similar Triangles
Two triangles are similar, if their corresponding angles are equal and their corresponding sides are in the same ratio. The ratio of any two corresponding sides in two equiangular triangles is always the same.
 Basic Proportionality Theorem
It states that if a line is drawn parallel to one side of a triangle to intersect the other two sides in the distinct points, the other two sides are divided in the same ratio. Conversely, If a line divides any more...
 Volume of Solids
The volume of the combined figures is obtained by finding the volume of each part separately and then adding them together.
 Cylinder
If 'r' be the radius and 'h' be the height of the cylinder, then
Volume of the cylinder \[=\,\pi \,\,{{r}^{2}}h\]
Cone
If 'r' be the radius and 'h' be the height of the cone, then
Volume of the cone \[=\frac{1}{3}\pi {{r}^{2}}h\]
Sphere
If 'r' be the radius of the sphere, then
Volume of the sphere \[=\frac{4}{3}\pi {{r}^{3}}\]
Hemisphere
If 'r' be the radius of the hemisphere, then
Volume of the hemisphere \[=\frac{2}{3}\pi {{r}^{3}}\]
We are familiar with some of the basic solids like cuboid, cone, cylinder, and sphere. In this chapter we will discuss about how to find the surface area and volume of these figures in our daily life, we come across number of solids made up of combinations of two or more of the basic solids.
 Surface Area of Solids
We may get the solids which may be combinations of cylinder and cone or cylinder and hemisphere or cone and hemisphere and so on. In such cases we find the surface area of each part separately and add them to get the surface area of entire solid.
 Cylinder
If 'r' is the radius and 'h' is the height of the cylinder, then
Curved surface area of the cylinder \[=2\pi rh\]
Total surface area of more...
Introduction
The word trigonometry is a Greek word consists of two parts 'trigon' and 'metron? which means measurements of the sides of the triangles. This was basically developed to find the solutions of the problem related to the triangles in the geometry. Initially we use to measure angles in terms of degree, but now we will use another unit of measurement of angles called radians. We have/ n radian \[={{180}^{o}}\]
\[{{1}^{o}}={{60}^{/}}\], where dash denotes minutes and 1' = 60", where the double dash denotes seconds. The relation between the radian and degree measure is given by:
1 radian \[=\left( \frac{{{180}^{o}}}{\pi } \right)\,and\,{{1}^{o}}\frac{\pi }{180}\]radians
 Trigonometric Functions
In previous classes we have studied about the trigonometric ratio's in which we have studied about the various ratios of the sides of the triangle. In this chapter we will extend our studies till the relation between the various trigonometric ratios which is called trigonometric function and we will measure the angles in terms of radians.
 Sign of Trigonometric Function in Different Quadrants
|
Relations between the Roots of the Quadratic Equation
If 
are the roots of the quadratic equation
, then the relation between the roots of the quadratic equation is given by,
Sum of the roots 
Product of the roots 
Formation of Quadratic Equations
If 
, the nature of graph for different values of D is: (a) If D
