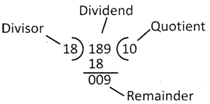
 Thus remainder = 9, Quotient = 10, and divisor = 18 Therefore, the mixed fraction for \[\frac{189}{18}=10\frac{9}{18}.\]
Thus remainder = 9, Quotient = 10, and divisor = 18 Therefore, the mixed fraction for \[\frac{189}{18}=10\frac{9}{18}.\]
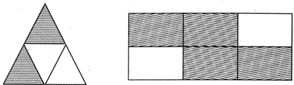 Fractional more...
Fractional more...
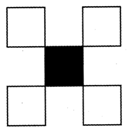 Explanation
The above figure has been divided into 5 equal parts. Out of 5 parts 1 part is shaded. Therefore, fractional representation of the shaded part \[\frac{1}{5}\] and numerator = 1, and denominator = 5.
Explanation
The above figure has been divided into 5 equal parts. Out of 5 parts 1 part is shaded. Therefore, fractional representation of the shaded part \[\frac{1}{5}\] and numerator = 1, and denominator = 5.
You need to login to perform this action.
You will be redirected in
3 sec
