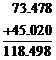5th Class

   Division of a Decimal by the Power of 10                     Step 1: Shift the point in the decimal left as many places as the number of zeroes the power of 10 contains.                 Step 2: If there are short of digits left to the point in the decimal, add zeroes left to it and follow the step 1.                     Divide 256.52 by 100.                   Explanation                 100 contains two zeroes, therefore, shift the point two digit left in the decimal                 Thus \[256.52\div 100=2.5652\text{ }.\]     Divide 3.25 by 10000.                   Explanation                 10000 contains 4 zeroes and 3.25 has only 1 digit left to the point so add ; zeroes left to it and shift the decimal 4 places left. more...

   Multiplication of Decimals by Power of 10                     Step1: Shift the point in the decimal right as many places as there are zeroes the power of 10 contains.                                                           .                 Step 2 : If there are short of digits to the right of the point in the decimal, add zeroes right to it and follow the first step.     Multiply 23.256 by 100.   Explanation                 Power of ten (here 100) contains two zeroes, so point will shift two digit   right.                 Thus \[23.256\times 100\text{ }=2325.6.\]     Multiply 27.5 and 1000.                 Here power of 10 contains three zeroes, therefore, decimal point will shift three digit right but the decimal contains only one digit right to the point so add two zeroes right to more...

  Subtraction of Decimals                     Step 1: Convert the minuend and subtrahend into like decimals.                 Step 2: Arrange the digits of minuend and subtrahend column wise one below other so that decimal points come in the same column.                 Step 3: Now subtract the digits column wise from right to left, write the difference directly below the respective digits and place a point in the point column.       Subtract: 83.455 and 23.201                                   Explanation                 Arrange the digits of 83.455 and 23.201 column wise and subtract.                 \[\begin{align}   & \,\,\,\,83.478 \\  & \underline{\frac{-23.201}{60.254}} \\ \end{align}\]                       Subtraction of a Decimal From a Whole Number Write the whole number in the decimal form then follow the steps given for subtraction of decimals. more...

   Addition of Decimals                     Step 1: Convert the addends into like decimals.                 Step 2: Arrange the addends one below other in columns so that decimal points come in the same column.                 Step 3: Now add the digits which are in the same column.         Add 73.478 and 45.02.                   Explanation                 45.02 can be written as 45.020                 Now 73.478 and 45.020 are like decimals. Arrange their digits column wise and add.                                      Addition of a Decimal and a Whole Number                 Write the whole number in the decimal form and follow the steps given for the addition of decimals.         Add more...

   Introduction                   In the previous chapter we have studied about the decimals. In this chapter we will study how to add two or more than two decimals, how to subtract a decimal from other decimal, how to multiply decimals, and how to divide a decimal by other decimal.  

   Comparison of Decimals     Step 1: Compare the integral parts of the decimals, the decimal having greater integral part is greater.                                 Step 2: If the integral parts are equal, compare the digits at tenth place in thedecimals. The decimal having greater digit at tenth place is greater.                   Step 3: If the digits at tenth place are equal, compare the digits at hundredth place and so on.         Compare 217.15 and 217.26.                   Explanation                 Integral part in 217.15 = 217                 Integral part in 217.26 = 217                 Thus both the decimals have same integral part. Therefore, compare the digits at tenths place.                 Digit at the tenth place in 217.15 = 1                 Digit at the tenth place in 217.26 = 2                 2 is greater than more...

     Conversion of Decimals         Conversion of Unlike Decimals into Like Decimals and Vice-Versa                 Step 1: Select the decimal which has the highest number of decimal places.                 Step 2: Now place the zeroes in the extreme right side in the other decimals so that they have equal number of digits right to the decimal point.         Convert 4.5, 9.03, 7.551, 2.1 into like decimals.                   Explanation                 The decimal 7.551 has the highest number of decimal places among the decimals 4.5, 9.03, 7.551, and 2.1.                 The decimal 4.5 has only one decimal place, thus put 2 zeroes in the extreme right side =4.500.                 The decimal 9.03 has only two decimal places, thus put 1 zeroes in the extreme right side = 9.030 more...

    Expanded Form of Decimals                     Expanded form of a decimal represents the addition of place values of the digits respected to their position in the decimal. For the example: Expanded form of 315.162 is \[300+10+5+\frac{1}{10}+\frac{6}{100}+\frac{2}{1000}.\]             Write the expanded form of the decimal 0.956                   Explanation                 \[0\frac{9}{10}+\frac{5}{100}+\frac{6}{1000}.\]                       Decimal Places                 The number of digits right to the point in a decimal is called decimal places of that decimal For example: In the decimal 26.345, there are three digits right to the point, therefore, the decimal 26.345 has three decimal places.     How many decimal places does the decimal 25.26 has?    Explanation                 There are two digits right to the point in more...

     Introduction                     A fraction with the denominator power of 10 (like 10, 100, 1000 etc.) is called decimal. It is expressed as a number using a point called decimal point. Decimal consist of two parts which are separated by a decimal point.                     Integral Part                 The part which is left to the decimal point is called integral part or whole number part. For example, in the decimal 896.3, 896 is the integral part.     Decimal Part                 The part which is right to the decimal point is called fractional part or decimal part.  For example: 45.683 is a decimal number in which 683 is fractional part or decimal part.                 Note: Decimal part read as separately one by one like 35.721 is read as thirty five more...

    Operation on the Fraction         Addition and Subtraction of Like Fractions    Like fractions have same denominator. In the operation of addition, numerators of the like fractions are added and their sum become the numerator for the required fraction and their common denominator becomes denominator. For the example:                 \[\frac{P}{Q}+\frac{R}{Q}+\frac{P+R}{Q}=\frac{S}{Q}\] (Where\[S=P+R\]). In the operation of subtraction, difference of numerators is found                 Ex: \[\frac{P}{Q}-\frac{R}{Q}=\frac{P-R}{Q}=\frac{S}{Q}\] (Where \[S=P-R\])         Add \[\frac{15}{7}\] and \[\frac{9}{7}\]                   Explanation            Addition of \[\frac{15}{7}\] and \[\frac{9}{7}=\frac{15}{7}+\frac{9}{7}\]                 \[=\frac{9+15}{7}=\frac{24}{7}.\]       Subtract \[\frac{9}{7}\] from \[\frac{15}{7}.\]                   Solution:                 \[\frac{15}{7}-\frac{9}{7}=\frac{15-9}{7}=\frac{6}{7}.\]       Addition and Subtraction of Unlike Fractions In the operation of addition of unlike fractions, LCM of more...