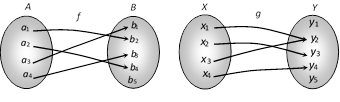
 Clearly, \[f:A\to B\] is a one-one function. But \[g:X\to Y\] is not one-one function because two distinct elements \[{{x}_{1}}\] and \[{{x}_{3}}\] have the same image under function \[g\].
(i) Method to check the injectivity of a function
Step I : Take two arbitrary elements \[x,\,\,y\] (say) in the domain of \[f\].
Step II : Put \[f(x)=f(y).\] more...
Clearly, \[f:A\to B\] is a one-one function. But \[g:X\to Y\] is not one-one function because two distinct elements \[{{x}_{1}}\] and \[{{x}_{3}}\] have the same image under function \[g\].
(i) Method to check the injectivity of a function
Step I : Take two arbitrary elements \[x,\,\,y\] (say) in the domain of \[f\].
Step II : Put \[f(x)=f(y).\] more...
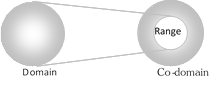 Range = For all values of \[x,\] all possible values of \[f(x)\].
Range = For all values of \[x,\] all possible values of \[f(x)\].
 (1) Methods for finding domain and range of function
(i) Domain
(a) Expression under even root (i.e., square root, fourth more...
(1) Methods for finding domain and range of function
(i) Domain
(a) Expression under even root (i.e., square root, fourth more...
 (2) Closed interval : Let a and b be two real numbers such that \[a<b,\] then the set of all real numbers lying between \[a\] and \[b\] including \[a\] and \[b\] is called a closed interval and is denoted by \[[a,\,\,b]\]. Thus, \[[a,\,\,b]=\{x\in R\,:\,a\le x\le b\}\]
(2) Closed interval : Let a and b be two real numbers such that \[a<b,\] then the set of all real numbers lying between \[a\] and \[b\] including \[a\] and \[b\] is called a closed interval and is denoted by \[[a,\,\,b]\]. Thus, \[[a,\,\,b]=\{x\in R\,:\,a\le x\le b\}\]
 (3) Open-Closed interval : It is denoted by \[[a,\,\,b]\] or \[(a,\,\,b]\] and \[[a,\,\,b]\] or \[(a,\,\,b]=\{x\in R\,:\,\,a<x\le b\}\].
(3) Open-Closed interval : It is denoted by \[[a,\,\,b]\] or \[(a,\,\,b]\] and \[[a,\,\,b]\] or \[(a,\,\,b]=\{x\in R\,:\,\,a<x\le b\}\].
You need to login to perform this action.
You will be redirected in
3 sec
