| Trigonometrical equation | General solution |
| \[\sin \theta =0\] | \[\theta =n\pi \] |
| \[\cos \theta =0\] | \[\theta =n\pi +\pi /2\] |
| more...
An equation involving one or more trigonometrical ratio of an unknown angle is called a trigonometrical equation
i.e., \[\sin x+\cos 2x=1\],\[(1-\tan \theta )(1+\sin 2\theta )=1+\tan \theta \], \[|\sec \left( \theta +\frac{\pi }{4} \right)|\text{ }=2\] etc.
A trigonometric equation is different from a trigonometrical identities. An identity is satisfied for every value of the unknown angle e.g.,\[{{\cos }^{2}}x=1-{{\sin }^{2}}x\]is true \[\forall x\in R\], while a trigonometric equation is satisfied for some particular values of the unknown angle.
(1) Roots of trigonometrical equation : The value of unknown angle (a variable quantity) which satisfies the given equation is called the root of an equation, e.g., \[\cos \theta =\frac{1}{2}\], the root is \[\theta ={{60}^{o}}\] or \[\theta ={{300}^{o}}\] because the equation is satisfied if we put \[\theta ={{60}^{o}}\]or \[\theta ={{300}^{o}}\].
(2) Solution of trigonometrical equations : A value of the unknown angle which satisfies the trigonometrical equation is called its more...
The function, \[f(x)\] is differentiable at point \[P,\] iff there exists a unique tangent at point \[P\]. In other words, \[f(x)\] is differentiable at a point \[P\] iff the curve does not have \[P\] as a corner point. i.e., "the function is not differentiable at those points on which function has jumps (or holes) and sharp edges.”
Let us consider the function \[f(x)=|x-1|\], which can be graphically shown,
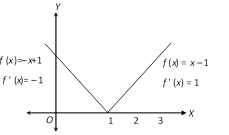 Which show \[f(x)\] is not differentiable at \[x=1\]. Since, \[f(x)\]has sharp edge at \[x=1\].
(i) Right hand derivative : Right hand derivative of \[f(x)\] at \[x=a\], denoted by \[f'(a+0)\] or \[f'(a+)\], is the \[\underset{h\to 0}{\mathop{\lim }}\,\frac{f(a+h)-f(a)}{h}\].
(ii) Left hand derivative : Left hand derivative of \[f(x)\] at \[x=a,\] denoted by \[f'(a-0)\] or \[f'(a-)\], is the \[\underset{h\to more...
Which show \[f(x)\] is not differentiable at \[x=1\]. Since, \[f(x)\]has sharp edge at \[x=1\].
(i) Right hand derivative : Right hand derivative of \[f(x)\] at \[x=a\], denoted by \[f'(a+0)\] or \[f'(a+)\], is the \[\underset{h\to 0}{\mathop{\lim }}\,\frac{f(a+h)-f(a)}{h}\].
(ii) Left hand derivative : Left hand derivative of \[f(x)\] at \[x=a,\] denoted by \[f'(a-0)\] or \[f'(a-)\], is the \[\underset{h\to more...
(1) Discontinuous function : A function \['f'\] which is not continuous at a point \[x=a\] in its domain is said to be discontinuous there at. The point \['a'\] is called a point of discontinuity of the function.
The discontinuity may arise due to any of the following situations.
(i) \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)\] or \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)\] or both may not exist
(ii) \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)\]as well as \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)\] may exist, but are unequal.
(iii)\[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)\] as well as \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)\] both may exist, but either of the two or both may not be equal to \[f(a)\].
Function \[f(x)\] is said to be
(1) Left continuous at \[x=a\] if \[\underset{x\to {{a}^{-}}}{\mathop{\text{lim}}}\,f(x)=f(a)\]
(2) Right continuous at \[x=a\] if \[\underset{x\to {{a}^{+}}}{\mathop{\text{lim}}}\,f(x)=f(a)\].
Thus a function \[f(x)\] is continuous at a point \[x=a\] if it is left continuous as well as right continuous at \[x=a.\]
Properties of continuous functions : Let \[f(x)\] and \[g(x)\] be two continuous functions at \[x=a.\]Then
(i) A function \[f(x)\] is said to be everywhere continuous if it is continuous on the entire real line R i.e. \[(-\infty ,\infty )\]. e.g., polynomial function, \[{{e}^{x}},\]\[\sin x,\,\cos x,\,\]constant, \[{{x}^{n}},\] \[|x-a|\] etc.
(ii) Integral function of a continuous function is a continuous function.
(iii) If \[g(x)\] is continuous at \[x=a\] and \[f(x)\] is continuous at \[x=g(a)\] then \[(fog)\,(x)\] is continuous at \[x=a\].
(iv) If \[f(x)\] is continuous in a closed interval \[[a,\,\,b]\] then more...
A function \[f(x)\] is said to be continuous at a point \[x=a\] of its domain if and only if it satisfies the following three conditions :
(1) \[f(a)\] exists. (\['a'\] lies in the domain of \[f\])
(2) \[\underset{x\to a}{\mathop{\lim }}\,\,f(x)\] exist i.e.\[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)\] or R.H.L. = L.H.L.
(3) \[\underset{x\to a}{\mathop{\lim }}\,f(x)=f(a)\] (limit equals the value of function).
Cauchy’s definition of continuity : A function \[f\] is said to be continuous at a point \[a\] of its domain \[D\] if for every \[\varepsilon >0\] there exists \[\delta >0\] (dependent on \[\varepsilon )\] such that \[|x-a|<\delta \] \[\Rightarrow |\,f(x)-f(a)|<\varepsilon .\]
Comparing this definition with the definition of limit we find that \[f(x)\] is continuous at \[x=a\] if \[\underset{x\to a}{\mathop{\lim }}\,f(x)\] exists and is equal to \[f(a)\] i.e., if \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)=f(a)=\underset{x\to a+}{\mathop{\lim }}\,f(x)\].
The word ‘continuous’ means without any break or gap. If the graph of a function has no break or gap or jump, then it is said to be continuous.
A function which is not continuous is called a discontinuous function. While studying graphs of functions, we see that graphs of functions \[\sin x\], \[x,\] \[\cos x\], \[{{e}^{x}}\] etc. are continuous but greatest integer function \[[x]\] has break at every integral point, so it is not continuous. Similarly \[\tan x,\,\,\cot x,\,\,\sec x\], \[\frac{1}{x}\] etc. are also discontinuous function.
Continuous function
 Discontinuous function
Discontinuous function 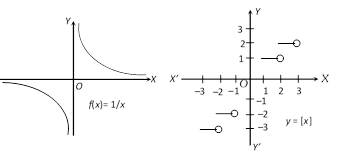
We shall divide the problems of evaluation of limits in five categories.
(1) Algebraic limits : Let \[f(x)\] be an algebraic function and \['a'\] be a real number. Then \[\underset{x\to a}{\mathop{\lim }}\,f(x)\] is known as an algebraic limit.
(i) Direct substitution method : If by direct substitution of the point in the given expression we get a finite number, then the number obtained is the limit of the given expression.
(ii) Factorisation method : In this method, numerator and denominator are factorised. The common factors are cancelled and the rest outputs the results.
(iii) Rationalisation method : Rationalisation is followed when we have fractional powers (like \[\frac{1}{2},\frac{1}{3}\] etc.) on expressions in numerator or denominator or in both. After rationalisation the terms are factorised which on cancellation gives the result.
(iv) Based on the form when \[x\to \infty \] : In more...
The following theorems are very useful for evaluation of limits if \[\underset{x\to 0}{\mathop{\lim }}\,f(x)=l\] and \[\underset{x\to 0}{\mathop{\lim }}\,g(x)=m\] (\[l\] and \[m\] are real numbers) then
(1) \[\underset{x\to a}{\mathop{\lim }}\,(f(x)+g(x))=l+m\,\] (Sum rule)
(2) \[\underset{x\to a}{\mathop{\lim }}\,(f(x)-g(x))=l-m\] (Difference rule)
(3) \[\underset{x\to a}{\mathop{\lim }}\,(f(x).g(x))=l.m\] (Product rule)
(4) \[\underset{x\to a}{\mathop{\lim }}\,k\,\,f(x)=k.l\] (Constant multiple rule)
(5) \[\underset{x\to a}{\mathop{\lim }}\,\,\frac{f(x)}{g(x)}=\frac{l}{m},m\ne 0\] (Quotient rule)
(6) If \[\underset{x\to a}{\mathop{\lim }}\,f(x)=+\infty \] or \[-\infty \], then \[\underset{x\to a}{\mathop{\lim }}\,\,\frac{1}{f(x)}=0\]
(7) \[\underset{x\to a}{\mathop{\lim }}\,\log \{f(x)\}=\log \,\{\underset{x\to a}{\mathop{\lim }}\,f(x)\}\]
(8) If \[f(x)\le g(x)\] for all \[x,\] then \[\underset{x\to a}{\mathop{\lim }}\,f(x)\le \underset{x\to a}{\mathop{\lim }}\,g(x)\]
(9) \[\underset{x\to a}{\mathop{\lim }}\,{{[f(x)]}^{g(x)}}={{\{\underset{x\to a}{\mathop{\lim }}\,f(x)\}}^{\underset{x\to a}{\mathop{\lim }}\,g(x)}}\]
(10) If \[p\] and \[q\] are integers, then \[\underset{x\to a}{\mathop{\lim }}\,{{(f(x))}^{p/q}}={{l}^{p/q}},\] provided \[{{(l)}^{p/q}}\] is a real number.
(11) If \[\underset{x\to a}{\mathop{\lim }}\,f(g(x))=f(\underset{x\to a}{\mathop{\lim more...
Let \[y=f(x)\] be a function of \[x\]. If at \[x=a,f(x)\] takes indeterminate form, then we consider the values of the function which are very near to \['a'\]. If these values tend to a definite unique number as \[x\] tends to \['a'\], then the unique number so obtained is called the limit of \[f(x)\] at \[x=a\] and we write it as \[\underset{x\to a}{\mathop{\lim }}\,f(x)\].
(1) Left hand and right hand limit : Consider the values of the functions at the points which are very near to \[a\] on the left of \[a\]. If these values tend to a definite unique number as \[x\] tends to \[a,\] then the unique number so obtained is called left-hand limit of \[f(x)\] at \[x=a\] and symbolically we write it as \[f(a-0)=\]\[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\,f(x)=\]\[\,\underset{h\to 0}{\mathop{\lim }}\,\,f(a-h)\].
Similarly we can define right-hand limit of \[f(x)\] at \[x=a\] which is expressed as \[f(a+0)=\underset{x\to {{a}^{+}}}{\mathop{\lim more...
Articles CategoriesArchive
Trending Articles
You need to login to perform this action. |