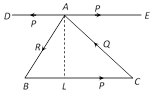
 The remaining two forces P along AD and P along BC form a couple, whose moment is, \[m=P.AL=BC.AL\]
Since, \[\frac{1}{2}(BC.AL)\] = Area of the \[\Delta ABC\]
\[\therefore \]Moment \[=BC.AL=2\](Area of \[\Delta ABC\]).
The remaining two forces P along AD and P along BC form a couple, whose moment is, \[m=P.AL=BC.AL\]
Since, \[\frac{1}{2}(BC.AL)\] = Area of the \[\Delta ABC\]
\[\therefore \]Moment \[=BC.AL=2\](Area of \[\Delta ABC\]).
 (2) Moment of couple : The moment of a couple is obtained in magnitude by multiplying the magnitude of one of the forces forming the couple and perpendicular distance between the lines of action of the force. The perpendicular distance between the forces is called the arm of the couple. The moment of more...
(2) Moment of couple : The moment of a couple is obtained in magnitude by multiplying the magnitude of one of the forces forming the couple and perpendicular distance between the lines of action of the force. The perpendicular distance between the forces is called the arm of the couple. The moment of more...
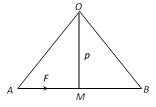 If F be a force acting at point A of a rigid body along the line AB and \[OM(=p)\] be the perpendicular distance of the fixed point O from AB, then the moment of force about O
\[=F.p=AB\times OM=2\left[ \frac{1}{2}(AB\times OM) \right]\]\[=2\text{ }(\text{Area of }\Delta AOB)\]
The S.I. unit of moment is Newton-meter \[(N-m)\].
(1) Sign of the moment : The moment of a force about a point measures the tendency of the force to cause rotation about that point. The tendency of the force \[{{F}_{1}}\] is to turn the lamina in the clockwise direction and of the force \[{{F}_{2}}\] is more...
If F be a force acting at point A of a rigid body along the line AB and \[OM(=p)\] be the perpendicular distance of the fixed point O from AB, then the moment of force about O
\[=F.p=AB\times OM=2\left[ \frac{1}{2}(AB\times OM) \right]\]\[=2\text{ }(\text{Area of }\Delta AOB)\]
The S.I. unit of moment is Newton-meter \[(N-m)\].
(1) Sign of the moment : The moment of a force about a point measures the tendency of the force to cause rotation about that point. The tendency of the force \[{{F}_{1}}\] is to turn the lamina in the clockwise direction and of the force \[{{F}_{2}}\] is more...
 The resultant \[R\] of two like parallel forces \[P\] and \[Q\] is equal in magnitude of the sum of the magnitudes of forces and \[R\] acts in the same direction as the forces \[P\] and \[Q\] and at the point on the line segment joining the point of action \[P\] and \[Q,\] which divides it in the ratio \[Q:P\] internally.
(2) Two unlike parallel forces : Two parallel forces are said to be unlike if they act in opposite directions.
If \[P\] and \[Q\] be two unlike parallel forces acting at \[A\] and \[B\] and \[P\] is greater in magnitude than \[Q\]. Then their resultant \[R\] acts in the same direction as \[P\] and more...
The resultant \[R\] of two like parallel forces \[P\] and \[Q\] is equal in magnitude of the sum of the magnitudes of forces and \[R\] acts in the same direction as the forces \[P\] and \[Q\] and at the point on the line segment joining the point of action \[P\] and \[Q,\] which divides it in the ratio \[Q:P\] internally.
(2) Two unlike parallel forces : Two parallel forces are said to be unlike if they act in opposite directions.
If \[P\] and \[Q\] be two unlike parallel forces acting at \[A\] and \[B\] and \[P\] is greater in magnitude than \[Q\]. Then their resultant \[R\] acts in the same direction as \[P\] and more...
 The converse of this theorem is also true.
The converse of this theorem is also true.
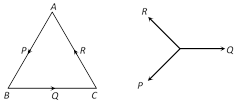 In triangle ABC, we have \[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=0\]
\[\Rightarrow P+Q+R=0\]
Hence the forces \[P,\,\,Q,\,\,R\] are in equilibrium.
Converse : If three forces acting at a point are in equilibrium, then they can be represented in magnitude and direction by the sides of a triangle, taken in order.
In triangle ABC, we have \[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=0\]
\[\Rightarrow P+Q+R=0\]
Hence the forces \[P,\,\,Q,\,\,R\] are in equilibrium.
Converse : If three forces acting at a point are in equilibrium, then they can be represented in magnitude and direction by the sides of a triangle, taken in order.
You need to login to perform this action.
You will be redirected in
3 sec
