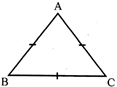
 A triangle has three vertex, three angles and three sides in above figure.
vertex be A, Band C
Angle be \[\angle ABC,\] \[\angle BCA,\] and \[\angle CAB,\]or \[\angle BAC\]
According to sides, type of triangle be
(a) Equilateral Triangle: All sides are equal
(b) Isosceles Triangle: Two sides are equal
(c) Scalene Triangle: All sides are different.
According to Angle, There are three types of triangles:
(a) Acute Angle Triangle
A triangle has three vertex, three angles and three sides in above figure.
vertex be A, Band C
Angle be \[\angle ABC,\] \[\angle BCA,\] and \[\angle CAB,\]or \[\angle BAC\]
According to sides, type of triangle be
(a) Equilateral Triangle: All sides are equal
(b) Isosceles Triangle: Two sides are equal
(c) Scalene Triangle: All sides are different.
According to Angle, There are three types of triangles:
(a) Acute Angle Triangle
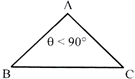 (b) Obtuse Angle Triangle
(b) Obtuse Angle Triangle
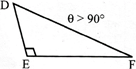
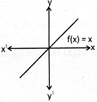 Discontinuous Function
Discontinuous Function
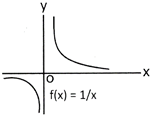
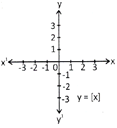 more...
more...
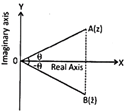 Hence, we have
\[\operatorname{Re}(z)=\frac{z+\overline{z}}{2}\] and \[\operatorname{Im}(z)=\frac{z-\overline{z}}{2i}\]
\[\Rightarrow \] Geometrically, the conjugate of z more...
Hence, we have
\[\operatorname{Re}(z)=\frac{z+\overline{z}}{2}\] and \[\operatorname{Im}(z)=\frac{z-\overline{z}}{2i}\]
\[\Rightarrow \] Geometrically, the conjugate of z more...
You need to login to perform this action.
You will be redirected in
3 sec
