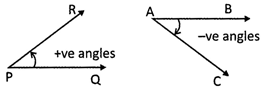
 more...
more...
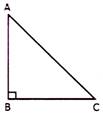
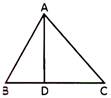 Area of right triangle \[=\frac{1}{2}\times \text{(perpendicular)}\times \text{Base}\] \[=\frac{1}{2}\times AB\times \text{BC}\]
Area of right triangle \[=\frac{1}{2}\times \text{(perpendicular)}\times \text{Base}\] \[=\frac{1}{2}\times AB\times \text{BC}\]
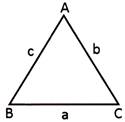
 Area of Triangle by Heron's Formula
Let a, b, c be the length of sides of a triangle
Area of Triangle by Heron's Formula
Let a, b, c be the length of sides of a triangle
 then area \[=\sqrt{s(s-a)(s-b)(s-c)}\]sq. unit where \[s=-\frac{1}{2}(a+b+c)\]
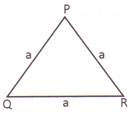
Area of Equilateral Triangle
then area \[=\sqrt{s(s-a)(s-b)(s-c)}\]sq. unit where \[s=-\frac{1}{2}(a+b+c)\]
Area of Equilateral Triangle
 Area \[=\frac{\sqrt{3}}{4}{{(side)}^{2}}=\frac{\sqrt{3}}{4}{{a}^{2}}\] Area of isosceles triangle
Area \[=\frac{\sqrt{3}}{4}{{(side)}^{2}}=\frac{\sqrt{3}}{4}{{a}^{2}}\] Area of isosceles triangle
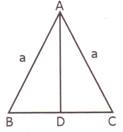 \[=\frac{1}{2}\times more...
\[=\frac{1}{2}\times more...
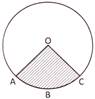 In the above given figure. OABC is a sector of the circle with centre 0. Here AC is the minor arc therefore, OABC is the minor sector and other plane sector is the major sector. Segment A segment of a circle is the region bounded by an arc and a chord. The segment containing minor arc is called a minor segment. While the segment containing the more...
In the above given figure. OABC is a sector of the circle with centre 0. Here AC is the minor arc therefore, OABC is the minor sector and other plane sector is the major sector. Segment A segment of a circle is the region bounded by an arc and a chord. The segment containing minor arc is called a minor segment. While the segment containing the more...
You need to login to perform this action.
You will be redirected in
3 sec
