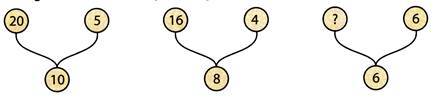
 (a) 8 (b) 6 (c) 4 (d) 12
Explanation (b):
Number in bottom = \[\sqrt{Product\text{ }of\text{ }numbers\text{ }on\text{ }the\text{ }top~}\]
\[\therefore 6=\sqrt{x\times 6}\Rightarrow 36=6x\Rightarrow x=6.\]
2. In the following question, a set of figures carrying certain characters, is given.
Assuming that the characters in each set follow a similar more...
(a) 8 (b) 6 (c) 4 (d) 12
Explanation (b):
Number in bottom = \[\sqrt{Product\text{ }of\text{ }numbers\text{ }on\text{ }the\text{ }top~}\]
\[\therefore 6=\sqrt{x\times 6}\Rightarrow 36=6x\Rightarrow x=6.\]
2. In the following question, a set of figures carrying certain characters, is given.
Assuming that the characters in each set follow a similar more...
 (a)
(a)  (b)
(b) 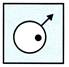 (c)
(c) 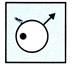 (d)
(d) 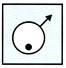 Explanation (c):
The arrow moves
Explanation (c):
The arrow moves  (a)
(a)  (b)
(b)  (c)
(c)  more...
more...
 (a) 16 (b) 22 (c) 28 (d) 32
Explanation (c):
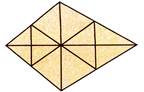
Let us label the components of given triangle as given below:
(a) 16 (b) 22 (c) 28 (d) 32
Explanation (c):
Let us label the components of given triangle as given below:
 Number of triangles made up of one component (triangle) each =12.
There names are : 1,1, 3,...., 12.
Number of triangles made up of two components each = 8.
Similarly, number of triangles made up of 3 components each = 4.
And number of triangles made up of 6 components each = 4.
Hence, number of all the triangles
= 12 + 8 + 4 + 4 = 28. more...
Number of triangles made up of one component (triangle) each =12.
There names are : 1,1, 3,...., 12.
Number of triangles made up of two components each = 8.
Similarly, number of triangles made up of 3 components each = 4.
And number of triangles made up of 6 components each = 4.
Hence, number of all the triangles
= 12 + 8 + 4 + 4 = 28. more...
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d) 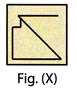 (a)
(a)  (b)
(b)  (c)
(c) 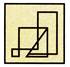 (d)
(d)  more...
more...
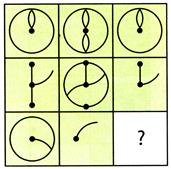 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)  Explanation (c):
In each row the third figure is more...
Explanation (c):
In each row the third figure is more...
You need to login to perform this action.
You will be redirected in
3 sec
