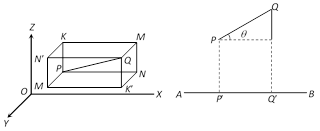
 Projection of PQ is \[P'Q'=PQ\cos \,\theta \]
\[=({{x}_{2}}-{{x}_{1}})\cos \alpha +({{y}_{2}}-{{y}_{1}})\cos \beta +({{z}_{2}}-{{z}_{1}})\cos \gamma \]
\[=({{x}_{2}}-{{x}_{1}})l+({{y}_{2}}-{{y}_{1}})m+({{z}_{2}}-{{z}_{1}})n\].
For x-axis,\[l=1,\,\,m=0,\,\,n=0\].
Hence, projection of PQ on x-axis \[={{x}_{2}}-{{x}_{1}}\].
Similarly, projection of PQ on y-axis \[={{y}_{2}}-{{y}_{1}}\] and projection of PQ on z-axis \[={{z}_{2}}{{z}_{1}}\].
Projection of PQ is \[P'Q'=PQ\cos \,\theta \]
\[=({{x}_{2}}-{{x}_{1}})\cos \alpha +({{y}_{2}}-{{y}_{1}})\cos \beta +({{z}_{2}}-{{z}_{1}})\cos \gamma \]
\[=({{x}_{2}}-{{x}_{1}})l+({{y}_{2}}-{{y}_{1}})m+({{z}_{2}}-{{z}_{1}})n\].
For x-axis,\[l=1,\,\,m=0,\,\,n=0\].
Hence, projection of PQ on x-axis \[={{x}_{2}}-{{x}_{1}}\].
Similarly, projection of PQ on y-axis \[={{y}_{2}}-{{y}_{1}}\] and projection of PQ on z-axis \[={{z}_{2}}{{z}_{1}}\].
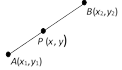 (1) Internal division : If \[P(x,y)\] divides the segment AB internally in the ratio of \[{{m}_{1}}:{{m}_{2}}\]\[\Rightarrow \]\[\frac{PA}{PB}=\frac{{{m}_{1}}}{{{m}_{2}}}\]
The co-ordinates of \[P(x,y)\] are
\[x=\frac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}}\] and \[y=\frac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}}\]
(2) External division : If \[P(x,y)\]divides the segment AB externally in the ratio of \[{{m}_{1}}:{{m}_{2}}\]\[\Rightarrow \]\[\frac{PA}{PB}=\frac{{{m}_{1}}}{{{m}_{2}}}\]\[\]
(1) Internal division : If \[P(x,y)\] divides the segment AB internally in the ratio of \[{{m}_{1}}:{{m}_{2}}\]\[\Rightarrow \]\[\frac{PA}{PB}=\frac{{{m}_{1}}}{{{m}_{2}}}\]
The co-ordinates of \[P(x,y)\] are
\[x=\frac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}}\] and \[y=\frac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}}\]
(2) External division : If \[P(x,y)\]divides the segment AB externally in the ratio of \[{{m}_{1}}:{{m}_{2}}\]\[\Rightarrow \]\[\frac{PA}{PB}=\frac{{{m}_{1}}}{{{m}_{2}}}\]\[\]
 The co-ordinates of \[P(x,y)\] are
\[x=\frac{{{m}_{1}}{{x}_{2}}-{{m}_{2}}{{x}_{1}}}{{{m}_{1}}-{{m}_{2}}}\] and \[y=\frac{{{m}_{1}}{{y}_{2}}-{{m}_{2}}{{y}_{1}}}{{{m}_{1}}-{{m}_{2}}}\]
The co-ordinates of \[P(x,y)\] are
\[x=\frac{{{m}_{1}}{{x}_{2}}-{{m}_{2}}{{x}_{1}}}{{{m}_{1}}-{{m}_{2}}}\] and \[y=\frac{{{m}_{1}}{{y}_{2}}-{{m}_{2}}{{y}_{1}}}{{{m}_{1}}-{{m}_{2}}}\] 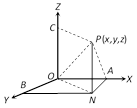 Then, \[PA=\sqrt{({{y}^{2}}+{{z}^{2}})}\]
\[PB=\sqrt{({{z}^{2}}+{{x}^{2}})}\]
\[PC=\sqrt{({{x}^{2}}+{{y}^{2}})}\]
Then, \[PA=\sqrt{({{y}^{2}}+{{z}^{2}})}\]
\[PB=\sqrt{({{z}^{2}}+{{x}^{2}})}\]
\[PC=\sqrt{({{x}^{2}}+{{y}^{2}})}\]
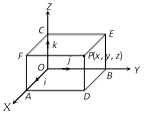 The planes \[XOY,YOZ\] and \[ZOX\]are known as xy-plane, yz-plane and zx-plane respectively.
Also,\[OA=x,\,\,OB=y,\,\,OC=z\].
The three co-ordinate planes (\[XOY,YOZ\] and\[ZOX\]) divide space into eight parts and these parts are called octants.
Sign of co-ordinates of a point : The signs of the co-ordinates of a point in three dimension follow the convention that all distances measured along or parallel to \[OX,\,\,OY,\,\,OZ\] will be positive and distances moved along or parallel to \[OX',\,\,OY',\,\,OZ'\] will be negative.
The planes \[XOY,YOZ\] and \[ZOX\]are known as xy-plane, yz-plane and zx-plane respectively.
Also,\[OA=x,\,\,OB=y,\,\,OC=z\].
The three co-ordinate planes (\[XOY,YOZ\] and\[ZOX\]) divide space into eight parts and these parts are called octants.
Sign of co-ordinates of a point : The signs of the co-ordinates of a point in three dimension follow the convention that all distances measured along or parallel to \[OX,\,\,OY,\,\,OZ\] will be positive and distances moved along or parallel to \[OX',\,\,OY',\,\,OZ'\] will be negative.
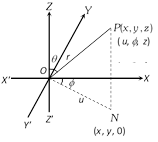 (2) Cylindrical co-ordinates : If the rectangular cartesian co-ordinates of \[P\] are \[(x,y,z),\] then those of \[N\] are \[(x,y,\text{ }0)\] and we can easily have the following relations : \[x=u\cos \,\phi ,\,\,y=u\sin \phi \] and \[z=z\].
Hence, \[{{u}^{2}}={{x}^{2}}+{{y}^{2}}\] and \[\varphi ={{\tan }^{-1}}(y/x)\].
Cylindrical co-ordinates of \[P\equiv (u,\phi ,z)\]
(3) Spherical polar co-ordinates : The measures of quantities \[r,\,\,\theta ,\,\,\phi \] are known as spherical or three dimensional polar co-ordinates of the point \[P\]. If the rectangular cartesian co-ordinates of \[P\] are \[(x,y,z)\] then \[z=r\cos \,\theta ,\,\,u=r\sin \,\theta \].
\[\therefore \] \[x=u\cos \,\phi =r\sin \,\theta \,\cos \,\phi ,\,\,y=u\sin \,\phi =r\,\sin \theta \,\sin \,\phi \] and \[z=r\cos \,\theta \]
Also, \[{{r}^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}\]and \[\tan \theta =\frac{u}{z}=\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}}{z};\,\,\tan \phi =\frac{y}{x}\].
(2) Cylindrical co-ordinates : If the rectangular cartesian co-ordinates of \[P\] are \[(x,y,z),\] then those of \[N\] are \[(x,y,\text{ }0)\] and we can easily have the following relations : \[x=u\cos \,\phi ,\,\,y=u\sin \phi \] and \[z=z\].
Hence, \[{{u}^{2}}={{x}^{2}}+{{y}^{2}}\] and \[\varphi ={{\tan }^{-1}}(y/x)\].
Cylindrical co-ordinates of \[P\equiv (u,\phi ,z)\]
(3) Spherical polar co-ordinates : The measures of quantities \[r,\,\,\theta ,\,\,\phi \] are known as spherical or three dimensional polar co-ordinates of the point \[P\]. If the rectangular cartesian co-ordinates of \[P\] are \[(x,y,z)\] then \[z=r\cos \,\theta ,\,\,u=r\sin \,\theta \].
\[\therefore \] \[x=u\cos \,\phi =r\sin \,\theta \,\cos \,\phi ,\,\,y=u\sin \,\phi =r\,\sin \theta \,\sin \,\phi \] and \[z=r\cos \,\theta \]
Also, \[{{r}^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}\]and \[\tan \theta =\frac{u}{z}=\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}}{z};\,\,\tan \phi =\frac{y}{x}\].
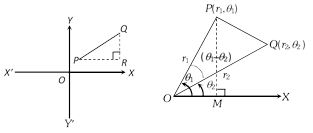 Then, \[{{(PQ)}^{2}}=r_{1}^{2}+r_{2}^{2}-2{{r}_{1}}{{r}_{2}}\cos ({{\theta }_{1}}-{{\theta }_{2}})\]
\[\therefore \] \[PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2{{r}_{1}}{{r}_{2}}\cos ({{\theta }_{1}}-{{\theta }_{2}})}\],
where \[{{\theta }_{1}}\] and \[{{\theta }_{2}}\] in radians.
Then, \[{{(PQ)}^{2}}=r_{1}^{2}+r_{2}^{2}-2{{r}_{1}}{{r}_{2}}\cos ({{\theta }_{1}}-{{\theta }_{2}})\]
\[\therefore \] \[PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2{{r}_{1}}{{r}_{2}}\cos ({{\theta }_{1}}-{{\theta }_{2}})}\],
where \[{{\theta }_{1}}\] and \[{{\theta }_{2}}\] in radians. 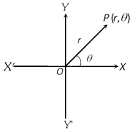 If \[(x,\,\,y)\] are the cartesian co-ordinates of a point P, then
\[x=r\,\cos \theta ;\,\,y=r\sin \theta \]
and \[r=\sqrt{{{x}^{2}}+{{y}^{2}}};\,\,\,\theta ={{\tan }^{-1}}\left( \frac{y}{x} \right)\].
If \[(x,\,\,y)\] are the cartesian co-ordinates of a point P, then
\[x=r\,\cos \theta ;\,\,y=r\sin \theta \]
and \[r=\sqrt{{{x}^{2}}+{{y}^{2}}};\,\,\,\theta ={{\tan }^{-1}}\left( \frac{y}{x} \right)\]. You need to login to perform this action.
You will be redirected in
3 sec
