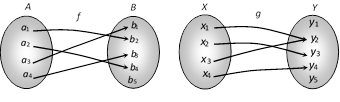
 Clearly, \[f:A\to B\] is a one-one function. But \[g:X\to Y\] is not one-one function because two distinct elements \[{{x}_{1}}\] and \[{{x}_{3}}\] have the same image under function \[g\].
(i) Method to check the injectivity of a function
Step I : Take two arbitrary elements \[x,\,\,y\] (say) in the domain of \[f\].
Step II : Put \[f(x)=f(y).\]
Step III : Solve \[f(x)=f(y).\] If \[f(x)=f(y)\] gives \[x=y\] only, then \[f:A\to B\] is a one-one function (or an injection). Otherwise not.
If function is given in the form of ordered pairs and if two ordered pairs do not have same second element then function is one-one.
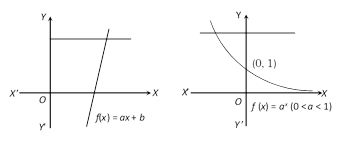
If the graph of the function \[y=f(x)\] is given and each line parallel to x-axis cuts the given curve at maximum one point then function is one-one. e.g.
Clearly, \[f:A\to B\] is a one-one function. But \[g:X\to Y\] is not one-one function because two distinct elements \[{{x}_{1}}\] and \[{{x}_{3}}\] have the same image under function \[g\].
(i) Method to check the injectivity of a function
Step I : Take two arbitrary elements \[x,\,\,y\] (say) in the domain of \[f\].
Step II : Put \[f(x)=f(y).\]
Step III : Solve \[f(x)=f(y).\] If \[f(x)=f(y)\] gives \[x=y\] only, then \[f:A\to B\] is a one-one function (or an injection). Otherwise not.
If function is given in the form of ordered pairs and if two ordered pairs do not have same second element then function is one-one.
If the graph of the function \[y=f(x)\] is given and each line parallel to x-axis cuts the given curve at maximum one point then function is one-one. e.g.
 (ii) Number of one-one functions (injections) : If \[A\] and \[B\] are finite sets having \[m\] and \[n\] elements respectively, then number of one-one functions from \[A\] to \[B\]\[=\left\{ \begin{align} & ^{n}{{P}_{m}},\,\,\,\text{if }n\ge m \\ & \,\,0\,\,\,\,,\,\,\,\text{if }n
· If function is given in the form of set of ordered pairs and the second element of atleast two ordered pairs are same then function is many-one.
· If the graph of \[y=f(x)\] is given and the line parallel to x-axis cuts the curve at more than one point then function is many-one.
(ii) Number of one-one functions (injections) : If \[A\] and \[B\] are finite sets having \[m\] and \[n\] elements respectively, then number of one-one functions from \[A\] to \[B\]\[=\left\{ \begin{align} & ^{n}{{P}_{m}},\,\,\,\text{if }n\ge m \\ & \,\,0\,\,\,\,,\,\,\,\text{if }n
· If function is given in the form of set of ordered pairs and the second element of atleast two ordered pairs are same then function is many-one.
· If the graph of \[y=f(x)\] is given and the line parallel to x-axis cuts the curve at more than one point then function is many-one.
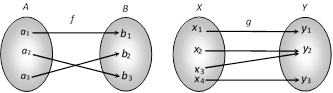
 (3) Onto function (surjection) : A function \[f:A\to B\] is onto if each element of B has its pre-image in A. Therefore, if \[{{f}^{-1}}(y)\in A,\,\,\forall y\in B\] then function is onto. In other words, Range of \[f=\] Co-domain of f. e.g. The following arrow-diagram shows onto function.
(3) Onto function (surjection) : A function \[f:A\to B\] is onto if each element of B has its pre-image in A. Therefore, if \[{{f}^{-1}}(y)\in A,\,\,\forall y\in B\] then function is onto. In other words, Range of \[f=\] Co-domain of f. e.g. The following arrow-diagram shows onto function.
 Number of onto function (surjection) : If A and B are two sets having \[m\] and \[n\] elements respectively such that \[1\le n\le m,\] then number of onto functions from A to B is \[\sum\limits_{r=1}^{n}{{{(-1)}^{n-r}}{{\,}^{n}}{{C}_{r}}{{r}^{m}}.}\]
(4) Into function : A function \[f:A\to B\] is an into function if there exists an element in B having no pre-image in A.
In more...
Number of onto function (surjection) : If A and B are two sets having \[m\] and \[n\] elements respectively such that \[1\le n\le m,\] then number of onto functions from A to B is \[\sum\limits_{r=1}^{n}{{{(-1)}^{n-r}}{{\,}^{n}}{{C}_{r}}{{r}^{m}}.}\]
(4) Into function : A function \[f:A\to B\] is an into function if there exists an element in B having no pre-image in A.
In more... 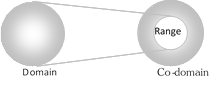 Range = For all values of \[x,\] all possible values of \[f(x)\].
Range = For all values of \[x,\] all possible values of \[f(x)\].
 (1) Methods for finding domain and range of function
(i) Domain
(a) Expression under even root (i.e., square root, fourth root etc.) \[\ge 0\]. Denominator \[\ne 0\].
If domain of \[y=f(x)\] and \[y=g\,(x)\] are \[{{D}_{1}}\] and \[{{D}_{2}}\] respectively then the domain of \[f(x)\pm g\,(x)\] or \[f(x).g\,(x)\] is \[{{D}_{1}}\cap {{D}_{2}}.\]
While domain of \[\frac{f(x)}{g(x)}\] is \[{{D}_{1}}\cap {{D}_{2}}-\{g(x)=0\}.\]
Domain of \[\left( \sqrt{f(x)} \right)={{D}_{1}}\cap \{x:f(x)\ge 0\}\]
(ii) Range : Range of \[y=f(x)\] is collection of all outputs \[f(x)\] corresponding to each real number in the domain.
(a) If domain \[\in \] finite number of points \[\Rightarrow \] range \[\in \] set of corresponding \[f(x)\] values.
(b) If domain \[\in R\] or \[R-\] [some finite points]. Then express \[x\] in terms of \[y\]. From this find \[y\] for \[x\] to be defined (i.e., find the values of \[y\] for which \[x\] exists).
(c) If domain \[\in \] a finite interval, find the least and greatest value for range using monotonicity.
(1) Methods for finding domain and range of function
(i) Domain
(a) Expression under even root (i.e., square root, fourth root etc.) \[\ge 0\]. Denominator \[\ne 0\].
If domain of \[y=f(x)\] and \[y=g\,(x)\] are \[{{D}_{1}}\] and \[{{D}_{2}}\] respectively then the domain of \[f(x)\pm g\,(x)\] or \[f(x).g\,(x)\] is \[{{D}_{1}}\cap {{D}_{2}}.\]
While domain of \[\frac{f(x)}{g(x)}\] is \[{{D}_{1}}\cap {{D}_{2}}-\{g(x)=0\}.\]
Domain of \[\left( \sqrt{f(x)} \right)={{D}_{1}}\cap \{x:f(x)\ge 0\}\]
(ii) Range : Range of \[y=f(x)\] is collection of all outputs \[f(x)\] corresponding to each real number in the domain.
(a) If domain \[\in \] finite number of points \[\Rightarrow \] range \[\in \] set of corresponding \[f(x)\] values.
(b) If domain \[\in R\] or \[R-\] [some finite points]. Then express \[x\] in terms of \[y\]. From this find \[y\] for \[x\] to be defined (i.e., find the values of \[y\] for which \[x\] exists).
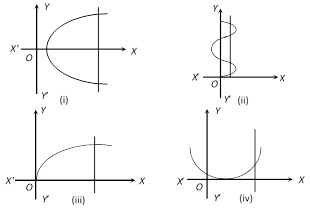
(c) If domain \[\in \] a finite interval, find the least and greatest value for range using monotonicity. 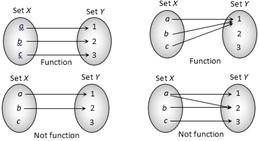 (2) Testing for a function by vertical line test : A relation \[f:A\to B\] is a function or not it can be checked by a graph of the relation. If it is possible to draw a vertical line which cuts the given curve at more than one point then the given relation is not a function and when this vertical line means line parallel to Y-axis cuts the curve at only one point then it is a function. Figure (iii) and (iv) represents a function.
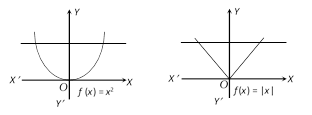
(2) Testing for a function by vertical line test : A relation \[f:A\to B\] is a function or not it can be checked by a graph of the relation. If it is possible to draw a vertical line which cuts the given curve at more than one point then the given relation is not a function and when this vertical line means line parallel to Y-axis cuts the curve at only one point then it is a function. Figure (iii) and (iv) represents a function.
 (3) Number of functions : Let \[X\] and \[Y\] be two finite sets having \[m\] and \[n\] elements respectively. Then each element of set \[X\]can be associated to any one of \[n\] elements of set \[Y\]. So, total number of functions from set \[X\] to set \[Y\] is \[{{n}^{m}}\].
(4) Value of the function : If \[y=f(x)\] is a function then to find its values at some value of \[x,\] say \[x=a,\] we directly substitute \[x=a\] in its given rule \[f(x)\] and it is denoted by \[f(a)\].
e.g. If \[f(x)={{x}^{2}}+1,\] then \[f(1)={{1}^{2}}+1=2,\] \[f(2)={{2}^{2}}+1=5,\] \[f(0)={{0}^{2}}+1=1\] etc.
(3) Number of functions : Let \[X\] and \[Y\] be two finite sets having \[m\] and \[n\] elements respectively. Then each element of set \[X\]can be associated to any one of \[n\] elements of set \[Y\]. So, total number of functions from set \[X\] to set \[Y\] is \[{{n}^{m}}\].
(4) Value of the function : If \[y=f(x)\] is a function then to find its values at some value of \[x,\] say \[x=a,\] we directly substitute \[x=a\] in its given rule \[f(x)\] and it is denoted by \[f(a)\].
e.g. If \[f(x)={{x}^{2}}+1,\] then \[f(1)={{1}^{2}}+1=2,\] \[f(2)={{2}^{2}}+1=5,\] \[f(0)={{0}^{2}}+1=1\] etc. 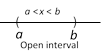 (2) Closed interval : Let a and b be two real numbers such that \[a<b,\] then the set of all real numbers lying between \[a\] and \[b\] including \[a\] and \[b\] is called a closed interval and is denoted by \[[a,\,\,b]\]. Thus, \[[a,\,\,b]=\{x\in R\,:\,a\le x\le b\}\]
(2) Closed interval : Let a and b be two real numbers such that \[a<b,\] then the set of all real numbers lying between \[a\] and \[b\] including \[a\] and \[b\] is called a closed interval and is denoted by \[[a,\,\,b]\]. Thus, \[[a,\,\,b]=\{x\in R\,:\,a\le x\le b\}\]
 (3) Open-Closed interval : It is denoted by \[[a,\,\,b]\] or \[(a,\,\,b]\] and \[[a,\,\,b]\] or \[(a,\,\,b]=\{x\in R\,:\,\,a<x\le b\}\].
(3) Open-Closed interval : It is denoted by \[[a,\,\,b]\] or \[(a,\,\,b]\] and \[[a,\,\,b]\] or \[(a,\,\,b]=\{x\in R\,:\,\,a<x\le b\}\].
You need to login to perform this action.
You will be redirected in
3 sec
