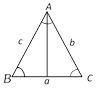
 where semiperimeter of triangle \[s=\frac{a+b+c}{2}\]
(3) When three sides and the circum-radius be given :
Area of triangle\[\Delta =\frac{abc}{4R}\], where R be the circum-radius of the triangle.
(4) When two angles and included side be given :
\[\Delta =\frac{1}{2}{{a}^{2}}\frac{\sin B\sin C}{\sin (B+C)}=\frac{1}{2}{{b}^{2}}\frac{\sin A\sin C}{\sin (A+C)}=\frac{1}{2}{{c}^{2}}\frac{\sin A\sin B}{\sin (A+B)}\]
where semiperimeter of triangle \[s=\frac{a+b+c}{2}\]
(3) When three sides and the circum-radius be given :
Area of triangle\[\Delta =\frac{abc}{4R}\], where R be the circum-radius of the triangle.
(4) When two angles and included side be given :
\[\Delta =\frac{1}{2}{{a}^{2}}\frac{\sin B\sin C}{\sin (B+C)}=\frac{1}{2}{{b}^{2}}\frac{\sin A\sin C}{\sin (A+C)}=\frac{1}{2}{{c}^{2}}\frac{\sin A\sin B}{\sin (A+B)}\] 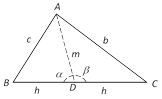 If \[\Delta \] be right angled, the mid point of hypotenuse is equidistant from the three vertices so that \[DA=DB=DC\].
\[\therefore {{b}^{2}}+{{c}^{2}}={{a}^{2}}\] which is pythagoras theorem. This theorem is very useful for solving problems of height and distance.
If \[\Delta \] be right angled, the mid point of hypotenuse is equidistant from the three vertices so that \[DA=DB=DC\].
\[\therefore {{b}^{2}}+{{c}^{2}}={{a}^{2}}\] which is pythagoras theorem. This theorem is very useful for solving problems of height and distance.  Similarly, we can deduct other projection formulae from sine rule.
(i)
Similarly, we can deduct other projection formulae from sine rule.
(i) 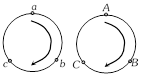
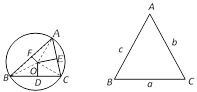 More generally, if \[R\] be the radius of the circumcircle of the triangle \[ABC,\,\,\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\].
More generally, if \[R\] be the radius of the circumcircle of the triangle \[ABC,\,\,\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]. | Functions | Periods |
| \[{{\sin }^{n}}x,\,\,{{\cos }^{n}}x,\,\,{{\sec }^{n}}x,\,\,\text{cose}{{\text{c}}^{n}}x\] | \[\left\{ \begin{matrix} \pi ;\,\,\text{if }n\text{ is even} \\ 2\pi ;\,\,\text{if }n\text{ is odd or fraction} \\ \end{matrix} \right.\] |
| \[{{\tan }^{n}}x,\,\,{{\cot }^{n}}x\] | \[\pi ;\,n\] is even or odd. |
| \[\sin (ax+b),\,\cos (ax+b)\] \[\sin (ax+b),\,\cos (ax+b)\] | \[2\pi /a\] |
| \[\tan (ax+b),\,\cot (ax+b)\] | \[\pi /a\] |
| \[\begin{align} & |\sin x|,\,|\cos x|,\,|\tan x|,\, \\ & |\cot x|,\,\,|\sec x|,\,\,|\text{cosec}\,x| \\ \end{align}\] | \[\pi \] |
| \[|\sin (ax+b)|,\,|\cos (ax+b)|,\] \[\,\sec |ax+b|,\,|\text{cosec }(ax+b)|\] \[|\tan (ax+b)|,\,|\cot (ax+b)|\] | \[\pi /a\] |
| \[x-[x]\] | 1 |
| Algebraic functions more...
(1) Check the validity of the given equation, e.g. \[2\sin \theta -\cos \theta =4\] can never be true for any \[\theta \] as the value \[(2\sin \theta -\cos \theta )\] can never exceeds \[\sqrt{{{2}^{2}}+{{(-1)}^{2}}}=\sqrt{5}\]. So there is no solution of this equation.
(2) Equation involving \[\sec \theta \] or \[\tan \theta \] can never have a solution of the form,\[(2n+1)\frac{\pi }{2}\].
Similarly, equations involving \[\text{cosec }\theta \] or \[\cot \theta \] can never have a solution of the form \[\theta =n\pi \]. The corresponding functions are undefined at these values of \[\theta \].
(3) If while solving an equation we have to square it, then the roots found after squaring must be checked whether they satisfy the original equation or not, e.g. let \[x=3\]. Squaring, we get \[{{x}^{2}}=9\] \[\therefore \] \[x=3\] and \[-\,3\] but \[x=-3\] does not satisfy the original equation \[x=3\].
(4) Do not cancel common factors involving the unknown angle on L.H.S. and R.H.S. because it may delete some solutions. In the equation \[\sin \theta (2\cos \theta -1)=\sin \theta {{\cos }^{2}}\theta \] if we cancel \[\sin \theta \] on both sides we get \[{{\cos }^{2}}\theta -2\cos \theta +1=0\] \[\Rightarrow {{(\cos \theta -1)}^{2}}=0\] \[\Rightarrow \cos \theta =1\Rightarrow \theta =2n\pi \]. But \[\theta =n\pi \] also satisfies the equation because it makes \[\sin \theta =0\]. So, the complete solution is \[\theta =n\pi ,\,n\in Z\].
(5) Any value of x which makes both R.H.S. and L.H.S. equal will be a root but the value of \[x\] for which \[\infty =\infty \] will not be a solution as it is an indeterminate form.
Hence, \[\cos x\ne 0\] for those equations which involve \[\tan x\]and \[\sec x\]whereas \[\sin x\ne 0\]for those which involve \[\cot x\]and \[\text{cosec}\,x\].
Also exponential function is always +ve and \[{{\log }_{a}}x\]is defined if \[x>0\], \[x\ne 0\] and \[a>0,a\ne 1\] \[\sqrt{f(x)}=+ve\] always and not \[\pm \,i.e.\] \[\sqrt{({{\tan }^{2}}x)}=\tan x\]and not \[\pm \tan x\].
(6) Denominator terms of the equation if present should never become zero at any stage while solving for any value of \[\theta \] contained in the answer.
(7) Sometimes the equation has some limitations also e.g., \[{{\cot }^{2}}\theta +\text{cose}{{\text{c}}^{2}}\theta =1\] can be true only if \[{{\cot }^{2}}\theta =0\] and \[\text{cose}{{\text{c}}^{2}}\theta =1\] simultaneously as \[\text{cose}{{\text{c}}^{2}}\theta \ge 1\]. Hence the solution is \[\theta =(2n+1)\pi /2\].
(8) If \[xy=xz\] then \[x(y-z)=0\Rightarrow \] either \[x=0\] or \[=\frac{1}{2}\sqrt{{{b}^{2}}+{{c}^{2}}+2bc\cos A}\] or both. But \[\frac{y}{x}=\frac{z}{x}\Rightarrow y=z\] only and not \[x=0\], as it will make \[\infty =\infty \]. Similarly if \[ay=az\], then it will also imply \[y=z\] only as \[a\ne 0\]being a constant.
Similarly \[x+y=x+z\Rightarrow y=z\] and \[x-y=x-z\Rightarrow y=z\]. Here we do not take \[x=0\] as in the above because \[x\] is an additive factor and not multiplicative factor.
(9) Student are advised to check whether all the roots obtained by them, satisfy the equation and lie in the domain of the variable of the given equation.
Suppose we have to find the principal value of \[\theta \] satisfying the equation \[\sin \theta =-\frac{1}{2}\].
Since \[\sin \theta \] is negative, \[\theta \] will be in 3rd or 4th quadrant. We can approach 3rd or 4th quadrant from two directions. If we take anticlockwise direction the numerical value of the angle will be greater than \[\pi \]. If we approach it in clockwise direction the angle will be numerically less than \[\pi \]. For principal value, we have to take numerically smallest angle. So for principal value.
(1) If the angle is in 1st or 2nd quadrant we must select anticlockwise direction and if the angle is in 3rd or 4th quadrant, we must select clockwise direction.
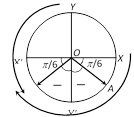 (2) Principal value is never numerically greater than \[\pi \].
(3) Principal value always lies in the first circle (i.e., in first rotation). On the above criteria, \[\theta \] will be \[-\frac{\pi }{6}\] or \[-\frac{5\pi }{6}.\] Between these two \[-\frac{\pi }{6}\] has the least numerical value. Hence \[-\frac{\pi }{6}\] is the principal value of \[\theta \] satisfying the equation \[\sin \theta =-\frac{1}{2}.\]
From the above discussion, the method for finding principal value can be summed up as follows :
(i) First draw a trigonometrical circle and mark the quadrant, in which the angle may lie.
(ii) Select anticlockwise direction for 1st and 2nd quadrants and select clockwise direction for 3rd and 4th quadrants.
(iii) Find the angle in the first rotation.
(iv) Select the numerically least angle. The angle thus found will be principal value.
(v) In case, two angles one with positive sign and the other with negative sign qualify for the numerically least angle, then it is the convention to select the angle with positive sign as principal value.
(2) Principal value is never numerically greater than \[\pi \].
(3) Principal value always lies in the first circle (i.e., in first rotation). On the above criteria, \[\theta \] will be \[-\frac{\pi }{6}\] or \[-\frac{5\pi }{6}.\] Between these two \[-\frac{\pi }{6}\] has the least numerical value. Hence \[-\frac{\pi }{6}\] is the principal value of \[\theta \] satisfying the equation \[\sin \theta =-\frac{1}{2}.\]
From the above discussion, the method for finding principal value can be summed up as follows :
(i) First draw a trigonometrical circle and mark the quadrant, in which the angle may lie.
(ii) Select anticlockwise direction for 1st and 2nd quadrants and select clockwise direction for 3rd and 4th quadrants.
(iii) Find the angle in the first rotation.
(iv) Select the numerically least angle. The angle thus found will be principal value.
(v) In case, two angles one with positive sign and the other with negative sign qualify for the numerically least angle, then it is the convention to select the angle with positive sign as principal value.
In \[a\cos \theta \,+b\sin \theta =c,\] put \[a=r\,\cos \alpha \] and \[b=r\,\sin \alpha \]where \[r=\sqrt{{{a}^{2}}+{{b}^{2}}}\] and \[|c|\le \sqrt{{{a}^{2}}+{{b}^{2}}}\]
Then,\[r\,(\cos \alpha \,\cos \theta +\sin \alpha \,\sin \theta )=c\]
\[\Rightarrow \,\,\cos (\theta -\alpha )=\frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\cos \beta \], (say) .....(i)
\[\Rightarrow \,\,\theta -\alpha =2n\pi \pm \beta \Rightarrow \,\theta =2n\pi \pm \beta +\alpha ,\] where \[\tan \alpha =\frac{b}{a}\] is the general solution.
Alternatively, putting \[a=r\,\sin \alpha \] and \[b=r\,\cos \alpha \],
where \[r=\sqrt{{{a}^{2}}+{{b}^{2}}}\] \[\Rightarrow \,\,\sin (\theta +\alpha )=\frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\sin \gamma \], (say)
\[\Rightarrow \,\,\theta +\alpha =n\pi +{{(-1)}^{n}}\gamma \]\[\Rightarrow \,\,\theta =n\pi +{{(-1)}^{n}}\gamma -\alpha ,\]
where \[\tan \alpha =\frac{a}{b}\] is the general solution.
\[(-\sqrt{{{a}^{2}}+{{b}^{2}}})\le \,a\cos \theta +b\sin \theta \le \,(\sqrt{{{a}^{2}}+{{b}^{2}}})\]
The general solution of \[a\cos x+b\sin x=c\] is
\[x=2n\pi +{{\tan }^{-1}}\left( \frac{b}{a} \right)\pm {{\cos }^{-1}}\left( \frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right)\].
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |