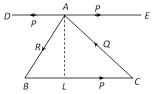
 The remaining two forces P along AD and P along BC form a couple, whose moment is, \[m=P.AL=BC.AL\]
Since, \[\frac{1}{2}(BC.AL)\] = Area of the \[\Delta ABC\]
\[\therefore \]Moment \[=BC.AL=2\](Area of \[\Delta ABC\]).
The remaining two forces P along AD and P along BC form a couple, whose moment is, \[m=P.AL=BC.AL\]
Since, \[\frac{1}{2}(BC.AL)\] = Area of the \[\Delta ABC\]
\[\therefore \]Moment \[=BC.AL=2\](Area of \[\Delta ABC\]).
| Integrand form | Substitution | |
| (i) | \[\sqrt{{{a}^{2}}-{{x}^{2}}},\frac{1}{\sqrt{{{a}^{2}}-{{x}^{2}}}},{{a}^{2}}-{{x}^{2}}\] | \[x=a\sin \theta ,\] or \[x=a\cos \theta \] |
| (ii) | \[\sqrt{{{x}^{2}}+{{a}^{2}}},\,\frac{1}{\sqrt{{{x}^{2}}+{{a}^{2}}}},\,{{x}^{2}}+{{a}^{2}}\] | \[x=a\tan \theta \] or \[x=a\sin \text{h}\theta \] |
| (iii) | \[\sqrt{{{x}^{2}}-{{a}^{2}},}\,\,\frac{1}{\sqrt{{{x}^{2}}-{{a}^{2}}}},\,\,{{x}^{2}}-{{a}^{2}}\] | \[x=a\sec \theta \] or \[x=a\cosh \theta \] |
| (iv) | \[\sqrt{\frac{x}{a+x}},\,\,\sqrt{\frac{a+x}{x}},\,\,\sqrt{x(a+x)},\,\,\frac{1}{\sqrt{x(a+x)}}\] | \[x=a{{\tan }^{2}}\theta \] |
| more...
Two equal unlike parallel forces which do not have the same line of action, are said to form a couple.
Example : Couples have to be applied in order to wind a watch, to drive a gimlet, to push a cork screw in a cork or to draw circles by means of pair of compasses.
(1) Arm of the couple : The perpendicular distance between the lines of action of the forces forming the couple is known as the arm of the couple.
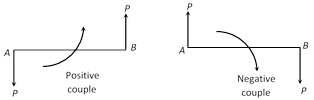
 (2) Moment of couple : The moment of a couple is obtained in magnitude by multiplying the magnitude of one of the forces forming the couple and perpendicular distance between the lines of action of the force. The perpendicular distance between the forces is called the arm of the couple. The moment of the couple is regarded as positive or negative according as it has a tendency to turn the body in the anticlockwise or clockwise direction.
Moment of a couple = Force \[\times \] Arm of the couple = P.p
(3) Sign of the moment of a couple : The moment of a couple is taken with positive or negative sign according as it has a tendency to turn the body in the anticlockwise or clockwise direction.
(2) Moment of couple : The moment of a couple is obtained in magnitude by multiplying the magnitude of one of the forces forming the couple and perpendicular distance between the lines of action of the force. The perpendicular distance between the forces is called the arm of the couple. The moment of the couple is regarded as positive or negative according as it has a tendency to turn the body in the anticlockwise or clockwise direction.
Moment of a couple = Force \[\times \] Arm of the couple = P.p
(3) Sign of the moment of a couple : The moment of a couple is taken with positive or negative sign according as it has a tendency to turn the body in the anticlockwise or clockwise direction.
The moment of a force about a point O is given in magnitude by the product of the forces and the perpendicular distance of O from the line of action of the force.
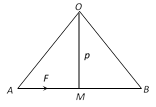 If F be a force acting at point A of a rigid body along the line AB and \[OM(=p)\] be the perpendicular distance of the fixed point O from AB, then the moment of force about O
\[=F.p=AB\times OM=2\left[ \frac{1}{2}(AB\times OM) \right]\]\[=2\text{ }(\text{Area of }\Delta AOB)\]
The S.I. unit of moment is Newton-meter \[(N-m)\].
(1) Sign of the moment : The moment of a force about a point measures the tendency of the force to cause rotation about that point. The tendency of the force \[{{F}_{1}}\] is to turn the lamina in the clockwise direction and of the force \[{{F}_{2}}\] is in the anticlockwise direction.
If F be a force acting at point A of a rigid body along the line AB and \[OM(=p)\] be the perpendicular distance of the fixed point O from AB, then the moment of force about O
\[=F.p=AB\times OM=2\left[ \frac{1}{2}(AB\times OM) \right]\]\[=2\text{ }(\text{Area of }\Delta AOB)\]
The S.I. unit of moment is Newton-meter \[(N-m)\].
(1) Sign of the moment : The moment of a force about a point measures the tendency of the force to cause rotation about that point. The tendency of the force \[{{F}_{1}}\] is to turn the lamina in the clockwise direction and of the force \[{{F}_{2}}\] is in the anticlockwise direction.
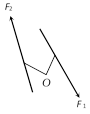 The usual convention is to regard the moment which is anticlockwise direction as positive and that in the clockwise direction as negative.
(2) Varignon's theorem : The algebraic sum of the moments of any two coplanar forces about any point in their plane is equal to the moment of their resultant about the same point.
The usual convention is to regard the moment which is anticlockwise direction as positive and that in the clockwise direction as negative.
(2) Varignon's theorem : The algebraic sum of the moments of any two coplanar forces about any point in their plane is equal to the moment of their resultant about the same point.
(1) Like parallel forces : Two parallel forces are said to be like parallel forces when they act in the same direction.
 The resultant \[R\] of two like parallel forces \[P\] and \[Q\] is equal in magnitude of the sum of the magnitudes of forces and \[R\] acts in the same direction as the forces \[P\] and \[Q\] and at the point on the line segment joining the point of action \[P\] and \[Q,\] which divides it in the ratio \[Q:P\] internally.
(2) Two unlike parallel forces : Two parallel forces are said to be unlike if they act in opposite directions.
If \[P\] and \[Q\] be two unlike parallel forces acting at \[A\] and \[B\] and \[P\] is greater in magnitude than \[Q\]. Then their resultant \[R\] acts in the same direction as \[P\] and acts at a point \[C\] on \[BA\] produced. Such that \[R=P-Q\] and \[P.CA=Q.CB\]
The resultant \[R\] of two like parallel forces \[P\] and \[Q\] is equal in magnitude of the sum of the magnitudes of forces and \[R\] acts in the same direction as the forces \[P\] and \[Q\] and at the point on the line segment joining the point of action \[P\] and \[Q,\] which divides it in the ratio \[Q:P\] internally.
(2) Two unlike parallel forces : Two parallel forces are said to be unlike if they act in opposite directions.
If \[P\] and \[Q\] be two unlike parallel forces acting at \[A\] and \[B\] and \[P\] is greater in magnitude than \[Q\]. Then their resultant \[R\] acts in the same direction as \[P\] and acts at a point \[C\] on \[BA\] produced. Such that \[R=P-Q\] and \[P.CA=Q.CB\]
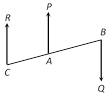 Then in this case \[C\] divides \[BA\] externally in the inverse ratio of the forces, \[\frac{P}{CB}=\frac{Q}{CA}=\frac{P-Q}{CB-CA}=\frac{R}{AB}\].
Then in this case \[C\] divides \[BA\] externally in the inverse ratio of the forces, \[\frac{P}{CB}=\frac{Q}{CA}=\frac{P-Q}{CB-CA}=\frac{R}{AB}\].
If three forces acting at a point be in equilibrium, each force is proportional to the sine of the angle between the other two. Thus if the forces are \[P,\,\,Q\] and \[R;\] \[\alpha ,\,\,\beta ,\,\,\gamma \] be the angles between \[Q\] and \[R,\,\,R\] and \[P,\,\,P\] and \[Q\] respectively, also the forces are in equilibrium, we have, \[\frac{P}{\sin \alpha }=\frac{Q}{\sin \beta }=\frac{R}{\sin \gamma }\].
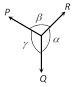 The converse of this theorem is also true.
The converse of this theorem is also true.
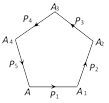
If any number of forces acting on a particle be represented in magnitude and direction by the sides of a polygon taken in order, the forces shall be in equilibrium.
If three forces, acting at a point, be represented in magnitude and direction by the sides of a triangle, taken in order, they will be in equilibrium.
Here \[\overrightarrow{AB}=P,\ \ \ \overrightarrow{BC}=Q,\ \ \overrightarrow{CA}=R\]
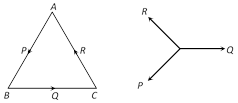 In triangle ABC, we have \[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=0\]
\[\Rightarrow P+Q+R=0\]
Hence the forces \[P,\,\,Q,\,\,R\] are in equilibrium.
Converse : If three forces acting at a point are in equilibrium, then they can be represented in magnitude and direction by the sides of a triangle, taken in order.
In triangle ABC, we have \[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=0\]
\[\Rightarrow P+Q+R=0\]
Hence the forces \[P,\,\,Q,\,\,R\] are in equilibrium.
Converse : If three forces acting at a point are in equilibrium, then they can be represented in magnitude and direction by the sides of a triangle, taken in order.
If two forces, acting at a point, be represented in magnitude and direction by the two sides of a parallelogram drawn from one of its angular points, their resultant is represented both in magnitude and direction of the parallelogram drawn through that point.
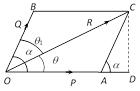
If \[OA\] and \[OB\] represent the forces \[P\] and \[Q\] acting at a point \[O\] and inclined to each other at an angle\[\alpha \]. If \[R\] is the resultant of these forces represented by the diagonal \[OC\] of the parallelogram \[OACB\] and \[R\] makes an angle \[\theta \] with \[P\].
i.e., \[\angle COA=\theta \], then \[{{R}^{2}}={{P}^{2}}+{{Q}^{2}}+2PQ\cos \alpha \] and \[\tan \theta =\frac{Q\sin \alpha }{P+Q\cos \alpha }\]
The angle \[{{\theta }_{1}}\] which the resultant \[R\] makes with the direction of the force \[Q\] is given by \[{{\theta }_{1}}={{\tan }^{-1}}\left( \frac{P\sin \alpha }{Q+P\cos \alpha } \right)\]
Case (i) : If \[P=Q\]
\[\therefore R=2P\cos \,\left( \frac{\alpha }{2} \right)\] and \[\tan \theta =\tan \left( \frac{\alpha }{2} \right)\] or \[\theta =\frac{\alpha }{2}\]
 Case (ii) : If \[\alpha =90{}^\circ \], i.e. forces are perpendicular
\[\therefore R=\sqrt{{{P}^{2}}+{{Q}^{2}}}\]and \[\tan \theta =\frac{Q}{P}\]
Case (iii) : If \[\alpha =0{}^\circ \], i.e. forces act in the same direction
\[\therefore {{R}_{\max }}=P+Q\]
Case (iv) : If \[\alpha =180{}^\circ \], i.e. forces act in opposite direction
\[\therefore {{R}_{\min }}=P-Q\]
Case (ii) : If \[\alpha =90{}^\circ \], i.e. forces are perpendicular
\[\therefore R=\sqrt{{{P}^{2}}+{{Q}^{2}}}\]and \[\tan \theta =\frac{Q}{P}\]
Case (iii) : If \[\alpha =0{}^\circ \], i.e. forces act in the same direction
\[\therefore {{R}_{\max }}=P+Q\]
Case (iv) : If \[\alpha =180{}^\circ \], i.e. forces act in opposite direction
\[\therefore {{R}_{\min }}=P-Q\]
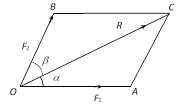
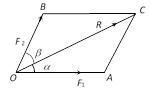 \[\mathbf{\lambda r\mu }\] theorem : The resultant of two forces acting at a point \[O\] in directions \[OA\] and \[OB\]represented in magnitudes by \[\lambda .OA\]and \[\mu .OB\] respectively is represented more...
\[\mathbf{\lambda r\mu }\] theorem : The resultant of two forces acting at a point \[O\] in directions \[OA\] and \[OB\]represented in magnitudes by \[\lambda .OA\]and \[\mu .OB\] respectively is represented more...
(1) (i) \[\int{{{x}^{n}}dx=\frac{{{x}^{n+1}}}{n+1}+c,\,n\ne -1}\]
(ii) \[\int{{{(ax+b)}^{n}}dx=\frac{1}{a}.\,\frac{{{(ax+b)}^{n+1}}}{n+1}}+c\], \[n\ne -1\]
(2) (i) \[\int{\frac{1}{x}dx=\log |x|+c}\]
(ii) \[\int{\frac{1}{ax+b}\,dx=\frac{1}{a}(\log |ax+b|)+c}\]
(3) \[\int{{{e}^{x}}dx={{e}^{x}}+c}\]
(4) \[\int{{{a}^{x}}dx=\frac{{{a}^{x}}}{{{\log }_{e}}a}+c}\]
(5) \[\int{\sin x\,dx=-\cos x+c}\]
(6) \[\int{\cos x\,dx=\sin x+c}\]
(7) \[\int{{{\sec }^{2}}}x\,dx=\tan x+c\]
(8) \[\int{\text{cos}\text{e}{{\text{c}}^{2}}x\,dx}=-\cot x+c\]
(9) \[\int{\sec x\,\tan x\,dx=\sec x+c}\]
(10) \[\int{\text{cosec}\,x\,\cot x\,dx=-\text{cosec}\,x+c}\]
(11) \[\int{\tan x\,dx}=-\log |\cos x|+c=\log |\sec x|+c\]
(12) \[\int{\cot x\,dx=\log |\sin x|+}c=-\log |\cos ec\,x|+c\]
(13) \[\int{\sec x\,dx=\log |\sec x+\tan x|+c=\log \tan \left( \frac{\pi }{4}+\frac{x}{2} \right)+c}\]
(14) \[\int{\text{cos}\text{ec}}\,x\,dx=\log |\text{cos}\text{ec}\,x-\cot x|+c=\log \tan \frac{x}{2}+c\]
(15) \[\int{\frac{dx}{\sqrt{1-{{x}^{2}}}}={{\sin }^{-1}}x+c=-{{\cos }^{-1}}x+c}\]
(16) \[\int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}={{\sin }^{-1}}\frac{x}{a}+c}=-{{\cos }^{-1}}\frac{x}{a}+c\]
(17) \[\int{\frac{dx}{1+{{x}^{2}}}={{\tan }^{-1}}x+c=-{{\cot }^{-1}}x+c}\]
(18) \[\int{\frac{dx}{{{a}^{2}}+{{x}^{2}}}=\frac{1}{a}{{\tan }^{-1}}\frac{x}{a}+c=\frac{-1}{a}{{\cot }^{-1}}\frac{x}{a}+c}\]
(19) \[\int{\frac{dx}{x\sqrt{{{x}^{2}}-1}}={{\sec }^{-1}}x+c}=-\cos e{{c}^{-1}}x+c\]
(20) \[\int{\frac{dx}{x\sqrt{{{x}^{2}}-{{a}^{2}}}}=\frac{1}{a}{{\sec }^{-1}}\frac{x}{a}+c}=\frac{-1}{a}\cos e{{c}^{-1}}\frac{x}{a}+c\]
In any of the fundamental integration formulae, if \[x\] is replaced by \[ax+b\], then the same formulae is applicable but we must divide by coefficient of \[x\] or derivative of \[(ax+b)\] i.e., \[a\]. In general, if \[\int{f(x)dx=\varphi (x)+c}\], then\[\int{f(ax+b)\,dx=\frac{1}{a}\varphi \,(ax+b)}+c\]
\[\int{\sin (ax+b)\,dx=\frac{-1}{a}}\cos (ax+b)+c,\]
\[\int{\sec (ax+b)\,dx=\frac{1}{a}\log |\sec (ax+b)+\tan (ax+b)|+c}\] etc.
Some more results :
(i) \[\int{\frac{1}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\log \left| \frac{x-a}{x+a} \right|+c=\frac{-1}{a}{{\coth }^{-1}}\frac{x}{a}+c}\], when \[x>a\]
(ii) \[\int{\frac{1}{{{a}^{2}}-{{x}^{2}}}dx=\frac{1}{2a}\log \left| \frac{a+x}{a-x} \right|+c=\frac{1}{a}{{\tanh }^{-1}}\frac{x}{a}+c}\], when \[x<a\]
(iii) \[\int{\frac{dx}{\sqrt{{{x}^{2}}-{{a}^{2}}}}=\log \{|x+\sqrt{{{x}^{2}}-{{a}^{2}}}|\}+c=\cos \,{{\text{h}}^{-1}}\left( \frac{x}{a} \right)}+c\]
(iv) \[\int{\frac{dx}{\sqrt{{{x}^{2}}+{{a}^{2}}}}=\log }\{|x+\sqrt{{{x}^{2}}+{{a}^{2}}}|\}+c=\sin {{\text{h}}^{-1}}\left( \frac{x}{a} \right)+c\]
(v) \[\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=\frac{1}{2}x\sqrt{{{a}^{2}}-{{x}^{2}}}+\frac{1}{2}{{a}^{2}}{{\sin }^{-1}}\left( \frac{x}{a} \right)+c}\]
(vi) \[\int_{{}}^{{}}{\sqrt{{{x}^{2}}-{{a}^{2}}}}dx=\frac{1}{2}x\sqrt{{{x}^{2}}-{{a}^{2}}}-\frac{1}{2}{{a}^{2}}\log \{x+\sqrt{{{x}^{2}}-{{a}^{2}}}\}+c\]\[=\frac{1}{2}x\sqrt{{{x}^{2}}-{{a}^{2}}}-\frac{1}{2}{{a}^{2}}{{\cosh }^{-1}}\left( \frac{x}{a} \right)+c\]
(vii) \[\int{\sqrt{{{x}^{2}}+{{a}^{2}}}dx=\frac{1}{2}x\sqrt{{{x}^{2}}+{{a}^{2}}}+\frac{1}{2}{{a}^{2}}\log \{x+\sqrt{{{x}^{2}}+{{a}^{2}}}\}+c}\]\[=\frac{1}{2}x\sqrt{{{x}^{2}}+{{a}^{2}}}+\frac{1}{2}{{a}^{2}}\sin {{\text{h}}^{-1}}\left( \frac{x}{a} \right)\]
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |