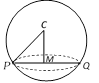
 Let C be the centre of the sphere and M be the foot of the perpendicular from C on the plane. Then M is the centre of the circle and radius of the circle is given by \[PM=\sqrt{C{{P}^{2}}-C{{M}^{2}}}\].
The centre M of the circle is the point of intersection of the plane and line CM which passes through C and is perpendicular to the given plane.
Centre : The foot of the perpendicular from the centre of the sphere to the plane is the centre of the circle.
\[{{(\text{Radius of circle})}^{\text{2}}}\text{= (Radius of sphere}{{)}^{\text{2}}}\text{-- (Perpendicular from centre of spheres on the plane}{{)}^{\text{2}}}\]
Great circle : The section of a sphere by a plane through the centre of the sphere is a great circle. Its centre and radius are the same as those of the given sphere.
Let C be the centre of the sphere and M be the foot of the perpendicular from C on the plane. Then M is the centre of the circle and radius of the circle is given by \[PM=\sqrt{C{{P}^{2}}-C{{M}^{2}}}\].
The centre M of the circle is the point of intersection of the plane and line CM which passes through C and is perpendicular to the given plane.
Centre : The foot of the perpendicular from the centre of the sphere to the plane is the centre of the circle.
\[{{(\text{Radius of circle})}^{\text{2}}}\text{= (Radius of sphere}{{)}^{\text{2}}}\text{-- (Perpendicular from centre of spheres on the plane}{{)}^{\text{2}}}\]
Great circle : The section of a sphere by a plane through the centre of the sphere is a great circle. Its centre and radius are the same as those of the given sphere. You need to login to perform this action.
You will be redirected in
3 sec
