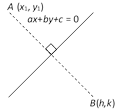 \[\frac{h-{{x}_{1}}}{a}=\frac{k-{{y}_{1}}}{b}=\frac{-2(a{{x}_{1}}+b{{y}_{1}}+c)}{{{a}^{2}}+{{b}^{2}}}\]
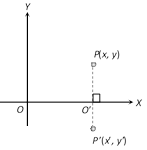
(2) The image of a point with respect to x-axis : Let \[P(x,y)\] be any point and \[{P}'({x}',\,{y}')\] its image after reflection in the x-axis, then \[{x}'=x\]
\[{y}'=-y,\] (\[\because \] \[{O}'\] is the mid point of P and \[{P}'\])
\[\frac{h-{{x}_{1}}}{a}=\frac{k-{{y}_{1}}}{b}=\frac{-2(a{{x}_{1}}+b{{y}_{1}}+c)}{{{a}^{2}}+{{b}^{2}}}\]
(2) The image of a point with respect to x-axis : Let \[P(x,y)\] be any point and \[{P}'({x}',\,{y}')\] its image after reflection in the x-axis, then \[{x}'=x\]
\[{y}'=-y,\] (\[\because \] \[{O}'\] is the mid point of P and \[{P}'\])
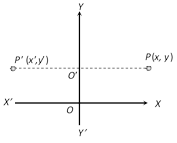
 (3) The image of a point with respect to y-axis : Let \[P(x,\,y)\] be any point and \[{P}'({x}',\,{y}')\] its image after reflection in the y-axis, then \[{x}'=-x\]
\[{y}'=y\], (\[\because \] \[{O}'\] is the mid point of P and \[{P}'\])
(3) The image of a point with respect to y-axis : Let \[P(x,\,y)\] be any point and \[{P}'({x}',\,{y}')\] its image after reflection in the y-axis, then \[{x}'=-x\]
\[{y}'=y\], (\[\because \] \[{O}'\] is the mid point of P and \[{P}'\])
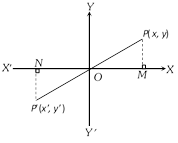
 (4) The image of a point with respect to the origin : Let \[P(x,y)\] be any point and \[{P}'({x}',\,{y}')\] be its image after reflection through the origin, then \[{x}'=-x\]
\[{y}'=-y\],(\[\because \] \[O\] is the mid point of P,\[{P}'\]).
(4) The image of a point with respect to the origin : Let \[P(x,y)\] be any point and \[{P}'({x}',\,{y}')\] be its image after reflection through the origin, then \[{x}'=-x\]
\[{y}'=-y\],(\[\because \] \[O\] is the mid point of P,\[{P}'\]).
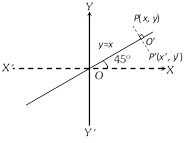
 (5) The image of a point with respect to the line \[y=x\] : Let \[P(x,\,y)\] be any point and \[{P}'({x}',\,{y}')\] be its image after reflection in the line \[y=x\], then \[{x}'=y\]
\[{y}'=x\], (\[\because \]\[{O}'\]is the mid point of P and \[{P}'\]).
(5) The image of a point with respect to the line \[y=x\] : Let \[P(x,\,y)\] be any point and \[{P}'({x}',\,{y}')\] be its image after reflection in the line \[y=x\], then \[{x}'=y\]
\[{y}'=x\], (\[\because \]\[{O}'\]is the mid point of P and \[{P}'\]).
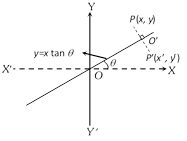
 (6) The image of a point with respect to the line \[y=x\tan \theta \] : Let \[P(x,\,y)\] be any point and \[{P}'({x}',\,{y}')\] be its image after reflection in the line \[y=x\tan \theta \], then
\[{x}'=x\cos 2\theta +y\sin 2\theta \]
\[{y}'=x\sin 2\theta -y\cos 2\theta \], (\[\because \] \[{O}'\] is the mid point of P and \[{P}'\])
(6) The image of a point with respect to the line \[y=x\tan \theta \] : Let \[P(x,\,y)\] be any point and \[{P}'({x}',\,{y}')\] be its image after reflection in the line \[y=x\tan \theta \], then
\[{x}'=x\cos 2\theta +y\sin 2\theta \]
\[{y}'=x\sin 2\theta -y\cos 2\theta \], (\[\because \] \[{O}'\] is the mid point of P and \[{P}'\])
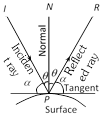 Here, IP = Incident Ray
PN = Normal to the surface
PR = Reflected Ray
Then, \[\angle IPN=\angle NPR\]
Angle of incidence = Angle of reflection
Here, IP = Incident Ray
PN = Normal to the surface
PR = Reflected Ray
Then, \[\angle IPN=\angle NPR\]
Angle of incidence = Angle of reflection 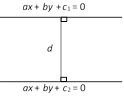 Second Method: The distance between the lines is \[d=\frac{\lambda }{\sqrt{({{a}^{2}}+{{b}^{2}})}}\],
Second Method: The distance between the lines is \[d=\frac{\lambda }{\sqrt{({{a}^{2}}+{{b}^{2}})}}\],
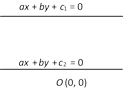 where (i) \[\lambda =|{{c}_{1}}-{{c}_{2}}|\], if they be on the same side of origin.
(ii) \[\lambda =|{{c}_{1}}|+|{{c}_{2}}|\], if the origin O lies between them.
Third method : Find the coordinates of any point on one of the given line, preferably putting \[x=0\] or \[y=0\]. Then the perpendicular distance of this point from the other line is the required distance between the lines.
where (i) \[\lambda =|{{c}_{1}}-{{c}_{2}}|\], if they be on the same side of origin.
(ii) \[\lambda =|{{c}_{1}}|+|{{c}_{2}}|\], if the origin O lies between them.
Third method : Find the coordinates of any point on one of the given line, preferably putting \[x=0\] or \[y=0\]. Then the perpendicular distance of this point from the other line is the required distance between the lines.
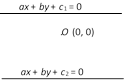 Distance between two parallel lines \[ax+by+{{c}_{1}}=0\],\[kax+kby+{{c}_{2}}=0\] is \[\frac{\left| \,{{c}_{1}}-\frac{{{c}_{2}}}{k}\, \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]. Distance between two non parallel lines is always zero.
Distance between two parallel lines \[ax+by+{{c}_{1}}=0\],\[kax+kby+{{c}_{2}}=0\] is \[\frac{\left| \,{{c}_{1}}-\frac{{{c}_{2}}}{k}\, \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]. Distance between two non parallel lines is always zero.
 (iii) If \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}>0\], then the bisector corresponding to \[''+''\] sign gives the obtuse angle bisector and the bisector corresponding to \[''-''\] sign is the bisector of acute angle between the lines.
(iv) If \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}<0\], then the bisector corresponding to \[''+''\] and \[''-''\] sign given the acute and obtuse angle bisectors respectively.
Bisectors are perpendicular to each other.
If \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}>0\], then the origin lies in obtuse angle and if \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}<0\], then the origin lies in acute angle.
(iii) If \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}>0\], then the bisector corresponding to \[''+''\] sign gives the obtuse angle bisector and the bisector corresponding to \[''-''\] sign is the bisector of acute angle between the lines.
(iv) If \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}<0\], then the bisector corresponding to \[''+''\] and \[''-''\] sign given the acute and obtuse angle bisectors respectively.
Bisectors are perpendicular to each other.
If \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}>0\], then the origin lies in obtuse angle and if \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}<0\], then the origin lies in acute angle.
You need to login to perform this action.
You will be redirected in
3 sec
