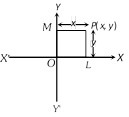
 Here, co-ordinates of the origin is (0, 0). The y co-ordinates of every point on x-axis is zero.
The x co-ordinates of every point on y-axis is zero.
Oblique axes : If both the axes are not perpendicular then they are called as oblique axes.
Here, co-ordinates of the origin is (0, 0). The y co-ordinates of every point on x-axis is zero.
The x co-ordinates of every point on y-axis is zero.
Oblique axes : If both the axes are not perpendicular then they are called as oblique axes.  The two lines \[XOX'\] and \[YOY'\] divide the plane in four quadrants. \[XOY,\text{ }YOX',\text{ }X'OY',\text{ }Y'OX\] are respectively called the first, the second, the third and the fourth quadrants. We assume the directions of \[OX,\,OY\] as positive while the directions of \[OX',\text{ }OY'\] as negative.
The two lines \[XOX'\] and \[YOY'\] divide the plane in four quadrants. \[XOY,\text{ }YOX',\text{ }X'OY',\text{ }Y'OX\] are respectively called the first, the second, the third and the fourth quadrants. We assume the directions of \[OX,\,OY\] as positive while the directions of \[OX',\text{ }OY'\] as negative. 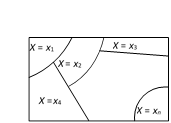 Now, since \[(X={{x}_{i}})\] is an event, we can talk of \[P(X={{x}_{i}})\]. If \[P(X={{x}_{i}})={{P}_{i}}\,(1\le i\le n)\], then the system of numbers.
\[\left( \begin{matrix}{{x}_{1}} & {{x}_{2}} & \cdots & {{x}_{n}} \\{{p}_{1}} & {{p}_{2}} & \cdots & {{p}_{n}} \\\end{matrix} \right)\] is said to be the probability distribution of the random variable X.
The expectation (mean) of the random variable X is defined as \[E(X)=\sum\limits_{i=1}^{n}{{{p}_{i}}{{x}_{i}}}\]and the variance of X is defined as \[\operatorname{var}(X)=\sum\limits_{i=1}^{n}{{{p}_{i}}{{({{x}_{i}}-E(X))}^{2}}}=\sum\limits_{i=1}^{n}{{{p}_{i}}x_{i}^{2}-{{(E(X))}^{2}}}\] .
(3) Binomial probability distribution : A random variable X which takes values \[0,\text{ }1,\text{ }2,\text{ }\ldots ,n\] is said to follow binomial distribution if its probability distribution function is given by \[P(X=r)={{\,}^{n}}{{C}_{r}}{{p}^{r}}{{q}^{n-r}},\,r=0,\,1,\,2,\,.....,\,n\] where \[p,\,\,q>0\] such that \[p+q=1\].
The notation \[X\tilde{\ }B\,(n,\,\,p)\] is generally used to denote that the random variable X follows binomial distribution with parameters n and p.
We have \[P(X=0)+P(X=1)+...+P(X=n)\].
\[={{\,}^{n}}{{C}_{0}}{{p}^{0}}{{q}^{n-0}}+{{\,}^{n}}{{C}_{1}}{{p}^{1}}{{q}^{n-1}}+...+{{\,}^{n}}{{C}_{n}}{{p}^{n}}{{q}^{n-n}}={{(q+p)}^{n}}={{1}^{n}}=1\]
Now probability of
(a) Occurrence of the event exactly r times \[P(X=r)={{\,}^{n}}{{C}_{r}}{{q}^{n-r}}{{p}^{r}}\].
(b) Occurrence of the event at least r times \[P(X\ge r)={{\,}^{n}}{{C}_{r}}{{q}^{n-r}}{{p}^{r}}+...+{{p}^{n}}=\sum\limits_{X=r}^{n}{^{n}{{C}_{X}}{{p}^{X}}{{q}^{n-X}}}\].
(c) Occurrence of the event at the most r times \[P(0\le X\le r)={{q}^{n}}+{{\,}^{n}}{{C}_{1}}{{q}^{n-1}}p+...+{{\,}^{n}}{{C}_{r}}{{q}^{n-r}}{{p}^{r}}=\sum\limits_{X=0}^{r}{{{p}^{X}}{{q}^{n-X}}}\].
Now, since \[(X={{x}_{i}})\] is an event, we can talk of \[P(X={{x}_{i}})\]. If \[P(X={{x}_{i}})={{P}_{i}}\,(1\le i\le n)\], then the system of numbers.
\[\left( \begin{matrix}{{x}_{1}} & {{x}_{2}} & \cdots & {{x}_{n}} \\{{p}_{1}} & {{p}_{2}} & \cdots & {{p}_{n}} \\\end{matrix} \right)\] is said to be the probability distribution of the random variable X.
The expectation (mean) of the random variable X is defined as \[E(X)=\sum\limits_{i=1}^{n}{{{p}_{i}}{{x}_{i}}}\]and the variance of X is defined as \[\operatorname{var}(X)=\sum\limits_{i=1}^{n}{{{p}_{i}}{{({{x}_{i}}-E(X))}^{2}}}=\sum\limits_{i=1}^{n}{{{p}_{i}}x_{i}^{2}-{{(E(X))}^{2}}}\] .
(3) Binomial probability distribution : A random variable X which takes values \[0,\text{ }1,\text{ }2,\text{ }\ldots ,n\] is said to follow binomial distribution if its probability distribution function is given by \[P(X=r)={{\,}^{n}}{{C}_{r}}{{p}^{r}}{{q}^{n-r}},\,r=0,\,1,\,2,\,.....,\,n\] where \[p,\,\,q>0\] such that \[p+q=1\].
The notation \[X\tilde{\ }B\,(n,\,\,p)\] is generally used to denote that the random variable X follows binomial distribution with parameters n and p.
We have \[P(X=0)+P(X=1)+...+P(X=n)\].
\[={{\,}^{n}}{{C}_{0}}{{p}^{0}}{{q}^{n-0}}+{{\,}^{n}}{{C}_{1}}{{p}^{1}}{{q}^{n-1}}+...+{{\,}^{n}}{{C}_{n}}{{p}^{n}}{{q}^{n-n}}={{(q+p)}^{n}}={{1}^{n}}=1\]
Now probability of
(a) Occurrence of the event exactly r times \[P(X=r)={{\,}^{n}}{{C}_{r}}{{q}^{n-r}}{{p}^{r}}\].
(b) Occurrence of the event at least r times \[P(X\ge r)={{\,}^{n}}{{C}_{r}}{{q}^{n-r}}{{p}^{r}}+...+{{p}^{n}}=\sum\limits_{X=r}^{n}{^{n}{{C}_{X}}{{p}^{X}}{{q}^{n-X}}}\].
(c) Occurrence of the event at the most r times \[P(0\le X\le r)={{q}^{n}}+{{\,}^{n}}{{C}_{1}}{{q}^{n-1}}p+...+{{\,}^{n}}{{C}_{r}}{{q}^{n-r}}{{p}^{r}}=\sum\limits_{X=0}^{r}{{{p}^{X}}{{q}^{n-X}}}\].
You need to login to perform this action.
You will be redirected in
3 sec
