A system of equations \[AX=B\] is called a homogeneous system if \[B=O\]. If \[B\ne O\], it is called a non-homogeneous system of equations.
e.g., \[2x+5y=0\]
\[3x-2y=0\]
is a homogeneous system of linear equations whereas the system of equations given by
e.g., \[2x+3y=5\]
\[x+y=2\]
is a non-homogeneous system of linear equations.
(1) Solution of Non-homogeneous system of linear equations
(i) Matrix method : If \[AX=B\], then \[X={{A}^{-1}}B\] gives a unique solution, provided A is non-singular.
But if A is a singular matrix i.e., if \[|A|=0\], then the system of equation \[AX=B\] may be consistent with infinitely many solutions or it may be inconsistent.
(ii) Rank method for solution of Non-Homogeneous system \[AX=B\]
(a) Write down A, B
(b) Write the augmented matrix \[[A:B]\]
(c) Reduce the augmented matrix to Echelon form by using elementary row operations.
(d) Find the number of non-zero rows in A and \[[A:B]\] to find the ranks of A and \[[A:B]\] respectively.
(e) If \[\rho (A)\ne \rho (A:B),\] then the system is inconsistent.
(f) \[\rho (A)=\rho (A:B)=\] the number of unknowns, then the system has a unique solution.
If \[\rho (A)=\rho (A:B)<\] number of unknowns, then the system has an infinite number of solutions.
(2) Solutions of a homogeneous system of linear equations : Let \[AX=O\] be a homogeneous system of 3 linear equations in 3 unknowns.
(a) Write the given system of equations in the form \[AX=O\] and write A.
(b) Find \[|A|\].
(c) If \[|A|\ne 0\], then the system is consistent and \[x=y=z=0\] is the unique solution.
(d) If \[|A|=0\], then the systems of equations has infinitely many solutions. In order to find that put \[z=K\] (any real number) and solve any two equations for \[x\] and \[y\] so obtained with \[z=K\] give a solution of the given system of equations.
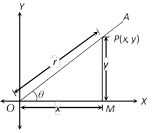\[\sin \theta =\frac{\text{Perpendicular}}{\text{Hypotenues}}=\frac{y}{r}\]
\[\frac{2n\pi \pm A}{2}\]
\[\tan \theta =\frac{\text{Perpendicular}}{\text{Base}}=\frac{y}{x}\]
\[\cot \theta =\frac{\text{Base}}{\text{Perpendicular}}=\frac{x}{y}\]
\[\sec \theta =\frac{\text{Hypotenues}}{\text{Base}}=\frac{r}{x}\]
\[\text{cosec}\theta =\frac{\text{Hypotenues}}{\text{Perpendicular}}=\frac{r}{y}\]
(1) Relation between trigonometric ratios (functions)
(i) \[\frac{\sqrt{4-\sqrt{2}-\sqrt{6}}}{2\sqrt{2}}\]
(ii) \[\tan \theta .\cot \theta =1\]
(iii) \[\cos \theta .\sec \theta =1\]
(iv) \[\tan \frac{A}{2}\] (v) \[\cot \theta =\frac{\cos \theta }{\sin \theta }\]
(2) Fundamental trigonometric identities
(i) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
(ii) \[1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta \]
(iii) \[1+{{\cot }^{2}}\theta =\text{cose}{{\text{c}}^{2}}\theta \]
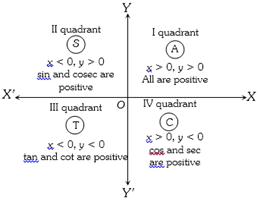
(3) Sign of trigonometrical ratios or functions : Their signs depends on the quadrant in which the terminal side of the angle lies.
In brief: A crude aid to memorise the signs of trigonometrical ratio in different quadrant. "Add Sugar To Coffee".
Algorithm : First determine the sign of the trigonometric function.
If \[\theta \] is measured from\[{X}'OX\] i.e., {(p ± q, 2p – q)} then retain the original name of the function.
If \[\theta \] is measured from \[{Y}'OY\] i.e.,\[\left\{ \frac{\pi }{2}\pm \theta ,\,\frac{3\pi }{2}\pm \theta \right\}\], then change sine to cosine, cosine to sine, tangent to cotangent, cot to tan, sec to cosec and cosec to sec.
(4) Variations in values of trigonometric functions in different quadrants : Let \[X'OX\] and \[YOY'\] be the coordinate axes. Draw a circle with centre at origin O and radius unity.
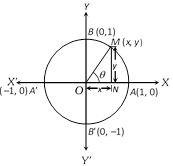Let \[M(x,y)\] be a point on the circle such that \[\angle AOM=\theta \] then \[x=\cos \theta \] and \[y=\sin \theta \]; \[-1\le \cos \theta \le \]1 and \[-1\le \sin \theta \le 1\] for all values of \[\theta \].
