| Characteristic of the function | \[{{b}^{2}}-4\,ac\,<\,0\] | \[{{b}^{2}}-4\,ac\,\,0\] | \[{{b}^{2}}-4\,ac>0\] |
| When 'a' is positive | more...

 more... more...
 (2) Infinitely Many Solutions
If the graph of the pair of linear equation is coincident, then the system of linear equation is said to have infinitely many solutions.
\[y=3x+2\,and\,6x-2y+4=0\]
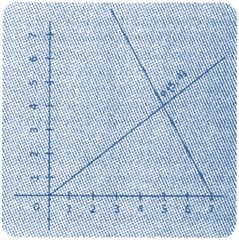
(2) Infinitely Many Solutions
If the graph of the pair of linear equation is coincident, then the system of linear equation is said to have infinitely many solutions.
\[y=3x+2\,and\,6x-2y+4=0\]
 (B) Inconsistent Equation
It has only one type of solution, which is no solution.
(1) No Solution
If the graph of the system of equation is more...
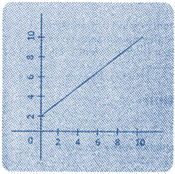
(B) Inconsistent Equation
It has only one type of solution, which is no solution.
(1) No Solution
If the graph of the system of equation is more...
 Solve the system of the equation given by \[\frac{4}{16x+24z}+\frac{12}{21x-14z}=\frac{1}{2}\] and \[\frac{14}{4x+6z}+\frac{4}{(3x-2z)}=2\]
(a) \[(x=2,z=1)\]
(b) \[(x=3,z=5)\]
(c) \[(x=-4,z=1)\]
(d) \[(x=1,z=-1)\]
(e) None of these
Answer: (a)
Solve the system of the equation given by \[\frac{4}{16x+24z}+\frac{12}{21x-14z}=\frac{1}{2}\] and \[\frac{14}{4x+6z}+\frac{4}{(3x-2z)}=2\]
(a) \[(x=2,z=1)\]
(b) \[(x=3,z=5)\]
(c) \[(x=-4,z=1)\]
(d) \[(x=1,z=-1)\]
(e) None of these
Answer: (a)

Articles CategoriesArchive
Trending Articles
You need to login to perform this action. |