JEE Main & Advanced

(1) Bond length            "The average distance between the centre of the nuclei of the two bonded atoms is called bond length".            It is expressed in terms of Angstrom (1 Å = \[{{10}^{-10}}\]m) or picometer (1pm = \[{{10}^{-12}}\]m).            In an ionic compound, the bond length is the sum of their ionic radii (\[d={{r}_{+}}+{{r}_{-}}\]) and in a covalent compound, it is the sum of their covalent radii (e.g., for HCl, \[d={{r}_{H}}+{{r}_{Cl}}\]).            Factors affecting bond length            (i) The bond length increases with increase in the size of the atoms. For example, bond length of \[H-X\] are in the order, \[HI>HBr>HCl>HF\].            (ii) The bond length decreases with the multiplicity of the bond. Thus, bond length of carbon-carbon bonds are in the order,  \[C\equiv C<C=C<CC\].            (iii) As an s-orbital is smaller in size, greater the s-character shorter is the hybrid orbital and hence shorter is the bond length. more...

  (1) Definition : The vector product or cross product of two vectors is defined as a vector having a magnitude equal to the product of the magnitudes of two vectors with the sine of angle between them, and direction perpendicular to the plane containing the two vectors in accordance with right hand screw rule.                                 \[\overrightarrow{C}=\overrightarrow{A}\times \overrightarrow{B}\] Thus, if \[\overrightarrow{A}\] and \[\overrightarrow{B}\] are two vectors, then their vector product written as \[\overrightarrow{A}\times \overrightarrow{B}\] is a vector \[\overrightarrow{C}\] defined by                                 \[\overrightarrow{C}=\overrightarrow{A}\times \overrightarrow{B}=AB\sin \theta \,\hat{n}\]                       The direction of \[\overrightarrow{A}\times \overrightarrow{B},\] i.e. \[\overrightarrow{C}\] is perpendicular to the plane containing vectors \[\overrightarrow{A}\] and \[\overrightarrow{B}\] and in the sense of more...

(1) Definition : The scalar product (or dot product) of two vectors is defined as the product of the magnitude of two vectors with cosine of angle between them.   Thus if there are two vectors \[\overrightarrow{A}\]and \[\overrightarrow{B}\] having angle \[\theta \] between them, then their scalar product written as \[\overrightarrow{A}\,.\,\overrightarrow{B}\] is defined as \[\overrightarrow{A}\,.\,\overrightarrow{B}\] \[=AB\,\cos \theta \]                                            (2) Properties : (i) It is always a scalar which is positive if angle between the vectors is acute (i.e., < 90°) and negative if angle between them is obtuse (i.e. 90°<q < 180°).         (ii) It is commutative, i.e. \[\overrightarrow{A}\,.\,\overrightarrow{B}\,=\,\overrightarrow{B}\,.\,\overrightarrow{A}\] (iii) It is distributive, i.e. \[\overrightarrow{A}\,.\,(\overrightarrow{B}+\overrightarrow{C})\,=\overrightarrow{A}\,.\,\overrightarrow{B}\,+\overrightarrow{A}\,.\,\overrightarrow{C}\] (iv) As by definition \[\overrightarrow{A}\,.\,\overrightarrow{B}=AB\,\cos \theta \] more...

\[\overrightarrow{R}={{\overrightarrow{R}}_{x}}+{{\overrightarrow{R}}_{y}}+{{\overrightarrow{R}}_{z}}q\] or  \[\overrightarrow{R}={{R}_{x}}\hat{i}+{{R}_{y}}\hat{j}+{{R}_{z}}\hat{k}\]     If \[\overrightarrow{R}\] makes an angle a with x axis, b with y axis and \[\gamma \]with z axis, then \[\Rightarrow q\] \[\cos \alpha =\frac{{{R}_{x}}}{R}=\frac{{{R}_{x}}}{\sqrt{R_{x}^{2}+R_{y}^{2}+R_{z}^{2}}}=l\] \[\Rightarrow \] \[\cos \beta =\frac{{{R}_{y}}}{R}=\frac{{{R}_{y}}}{\sqrt{R_{x}^{2}+R_{y}^{2}+R_{z}^{2}}}=m\] \[\Rightarrow \] \[\cos \gamma =\frac{{{R}_{z}}}{R}=\frac{{{R}_{z}}}{\sqrt{R_{x}^{2}+R_{y}^{2}+R_{z}^{2}}}=n\] Where l, m, n are called Direction Cosines of the vector \[\overrightarrow{R}\] and \[{{l}^{2}}+{{m}^{2}}+{{n}^{2}}=\]\[{{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =\frac{R_{x}^{2}+R_{y}^{2}+R_{z}^{2}}{R_{x}^{2}+R_{y}^{2}+R_{z}^{2}}=1\] Note :

• When a point P have coordinate (x, y, z) then its position vector \[\overrightarrow{OP}=x\hat{i}+y\hat{j}+z\hat{k}\]
• When a particle moves from point (x1, y1, z1) to (x2, y2, z2) then its displacement vector

\[\overset{\to }{\mathop{r}}\,=({{x}_{2}}-{{x}_{1}})\,\hat{i}+({{y}_{2}}-{{y}_{1}})\hat{j}+({{z}_{2}}-{{z}_{1}})\hat{k}\]    

The phenomenon of resonance was put forward by Heisenberg to explain the properties of certain molecules.                             In case of certain molecules, a single Lewis structure cannot explain all the properties of the molecule. The molecule is then supposed to have many structures, each of which can explain most of the properties of the molecule but none can explain all the properties of the molecule. The actual structure is in between of all these contributing structures and is called resonance hybrid and the different individual structures are called resonating structures or canonical forms. This phenomenon is called resonance. To illustrate this, consider a molecule of ozone \[{{O}_{3}}\]. Its structure can be written as \[\underset{(a)}{\mathop{\begin{array}{*{35}{l}}    \,\,\,\,\,\,O  \\    {}  \\    O\,\,\,\,\,\,\,\,O  \\ more...

Consider a vector \[\overrightarrow{R}\,\] in X-Y plane as shown in fig.  If we draw orthogonal vectors \[{{\overrightarrow{R}}_{x}}\] and \[{{\overrightarrow{R}}_{y}}\] along x and \[y\]axes respectively, by law of vector addition, \[\vec{R}={{\vec{R}}_{x}}+{{\vec{R}}_{y}}\]              Now as for any vector \[\overrightarrow{A}=A\,\hat{n}\]  so, \[{{\overrightarrow{R}}_{x}}=\hat{i}{{R}_{x}}\] and \[{{\overrightarrow{R}}_{y}}=\hat{j}{{R}_{y}}\] so \[\overrightarrow{R}=\hat{i}{{R}_{x}}+\hat{j}{{R}_{y}}\]                   ...(i) But from figure \[{{R}_{x}}=R\cos \theta \]                                           ...(ii)       and \[{{R}_{y}}=R\sin \theta \]                                                              ...(iii) Since R and q are usually known, Equation (ii) and (iii) give the magnitude of the components of \[\overrightarrow{R}\] along x and y-axes respectively. Here it is worthy to note once more...

Since, \[\overrightarrow{A}-\overrightarrow{B}=\overrightarrow{A}+(-\overrightarrow{B})\]  and   \[|\overrightarrow{A}+\overrightarrow{B}|\,=\, \sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }\] \[\Rightarrow \] \[|\overrightarrow{A}-\overrightarrow{B}|\,=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \,({{180}^{o}}-\theta )}\]                Since, \[\cos \,(180-\theta )=-\cos \theta \] \[\Rightarrow \] \[|\overrightarrow{A}-\overrightarrow{B}|\,=\,\sqrt{{{A}^{2}}+{{B}^{2}}-2AB\cos \theta }\]   \[\tan {{\alpha }_{1}}=\frac{B\sin \theta }{A+B\cos \theta }\] and \[\tan {{\alpha }_{2}}=\frac{B\sin \,(180-\theta )}{A+B\cos \,(180-\theta )}\] But \[\sin (180-\theta )=\sin \theta \] and \[\cos (180-\theta )=-\cos \theta \] \[\Rightarrow \] \[\tan {{\alpha }_{2}}=\frac{B\sin \theta }{A-B\cos \theta }\]    

The concept of hybridization was introduced by Pauling and Slater. HybridizationIt is defined as the intermixing of dissimilar orbitals of the same atom but having slightly different energies to form same number of new orbitals of equal energies and identical shapes. The new orbitals so formed are known as hybrid orbitals.          Characteristics of hybridization            (1) Only orbitals of almost similar energies and belonging to the same atom or ion undergoes hybridization.            (2) Hybridization takes place only in orbitals, electrons are not involved in it.            (3) The number of hybrid orbitals produced is equal to the number of pure orbitals, mixed during hybridization.            (4) In the excited state, the number of unpaired electrons must correspond to the oxidation state of the central atom in the molecule.            (5) Both half filled orbitals or fully filled orbitals of equivalent energy can involve in hybridization.            (6) Hybrid more...

It was developed by Heitler and London in 1927 and modified by Pauling and Slater in 1931.                             (1) To form a covalent bond, two atoms must come close to each other so that orbitals of one overlaps with the other.            (2) Orbitals having unpaired electrons of anti spin overlaps with each other.                             (3) After overlapping a new localized bond orbital is formed which has maximum probability of finding electrons.                             (4) Covalent bond is formed due to electrostatic attraction between radii and the accumulated electrons cloud and by attraction between spins of anti spin electrons.                             (5) Greater is the overlapping, lesser will be the bond length, more will be attraction and more will be bond energy and the stability of bond will also be high.                           (6) The extent of overlapping depends upon: Nature of orbitals involved in overlapping, and nature of overlapping.                             (7) more...

         ?The product of magnitude of negative or positive charge (q) and the distance (d) between the centres of positive and negative charges is called dipole moment?.            \[\mu =Electric\text{ }charge\times bond\text{ }length\] As q is in the order of \[{{10}^{-10}}\] esu and d is in the order of \[{{10}^{-8}}\] cm, m is in the order of \[{{10}^{-18}}\] esu cm. Dipole moment is measured in "Debye" (D) unit. \[1D={{10}^{-18}}\] esu cm = \[3.33\times {{10}^{-30}}\] coulomb metre (In S.I. unit).            Dipole moment is indicated by an arrow having a symbol  pointing towards the negative end. Dipole moment has both magnitude and direction and therefore it is a vector quantity.            Symmetrical polyatomic molecules are not polar so they do not have any value of dipole moment.          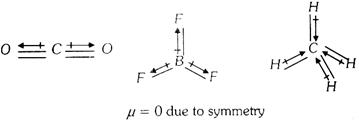Unsymmetrical polyatomic molecules always have net value of dipole moment, thus such molecules are polar in more...