 (2) The number of collisions taking place in unit time per unit volume, called collision frequency (z).
(i) The number of collision made by a single molecule with other molecules per unit time are given by, \[{{Z}_{A}}=\sqrt{2}\pi {{\sigma }^{2}}{{u}_{\text{av}\text{.}}}n\]
where n is the number of molecules per unit molar volume,
\[n=\frac{\text{Avogadro number(}{{N}_{0}}\text{)}}{{{V}_{m}}}=\frac{6.02\times {{10}^{23}}}{0.0224}{{m}^{-3}}\]
(ii) The total number of bimolecular collision per unit time are given by, \[{{Z}_{AA}}=\frac{1}{\sqrt{2}}\pi {{\sigma }^{2}}{{u}_{\text{av}.}}{{n}^{2}}\]
(iii) If the collisions involve two unlike molecules, the number of bimolecular collision are given by,
\[{{Z}_{AB}}=\sigma _{AB}^{2}{{\left[ 8\pi RT\frac{({{M}_{A}}+{{M}_{B}})}{{{M}_{A}}{{M}_{B}}} \right]}^{1/2}}\]
where, \[{{\sigma }_{AB}}=\frac{{{\sigma more...
(2) The number of collisions taking place in unit time per unit volume, called collision frequency (z).
(i) The number of collision made by a single molecule with other molecules per unit time are given by, \[{{Z}_{A}}=\sqrt{2}\pi {{\sigma }^{2}}{{u}_{\text{av}\text{.}}}n\]
where n is the number of molecules per unit molar volume,
\[n=\frac{\text{Avogadro number(}{{N}_{0}}\text{)}}{{{V}_{m}}}=\frac{6.02\times {{10}^{23}}}{0.0224}{{m}^{-3}}\]
(ii) The total number of bimolecular collision per unit time are given by, \[{{Z}_{AA}}=\frac{1}{\sqrt{2}}\pi {{\sigma }^{2}}{{u}_{\text{av}.}}{{n}^{2}}\]
(iii) If the collisions involve two unlike molecules, the number of bimolecular collision are given by,
\[{{Z}_{AB}}=\sigma _{AB}^{2}{{\left[ 8\pi RT\frac{({{M}_{A}}+{{M}_{B}})}{{{M}_{A}}{{M}_{B}}} \right]}^{1/2}}\]
where, \[{{\sigma }_{AB}}=\frac{{{\sigma more...
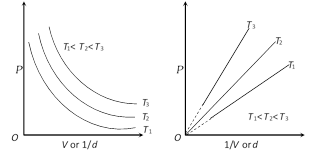
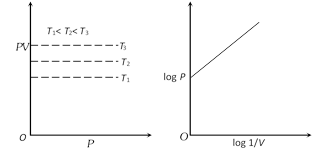 more...
more...
You need to login to perform this action.
You will be redirected in
3 sec
