SQUARE & SQUARE ROOTS
FUNDAMENTALS
Square and Square Root
- Square: If a number is multiplied by itself, the product so obtained is called the square of that number.
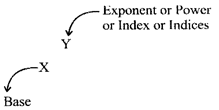
- For a given number x, the square of x is\[\left( x\times x \right)\], denoted by\[{{x}^{2}}\].
e.g., \[{{\left( 4 \right)}^{2}}=4\times 4=16,{{\left( 5 \right)}^{2}}=5\times 5=25,{{\left( 12 \right)}^{2}}=12\times 12=144\]
Perfect squares or Square number;"
- A perfect square is a number that can be expressed as the product of two equal integers.
- It is always expressible as the product of equal factors.
e.g., \[144=2\times 2\times 2\times 2\times 3\times 3={{4}^{2}}\times {{3}^{2}}={{(12)}^{2}}\]
\[81=3\times 3\times 3\times 3={{3}^{2}}\times {{3}^{2}}={{\left( 9 \right)}^{2}}\]
Example:- Show that 300 is not a perfect square.
Solution:- Resolving 300 into prime factors, we get \[300=2\times 2\times 5\times 5\times 3\]
Making pairs of equal factors, we find that the digit 3 is
more...
According more...
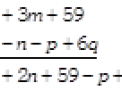Example 2- Add: \[9{{x}^{3}}+6{{x}^{5}}-8+16{{x}^{2}}\] and \[10{{x}^{8}}6{{x}^{2}}+9{{x}^{3}}-3x\]
Solution: Writing the given expressions in descending powers of x in the form of rows with like terms below each other and adding column wise, we get:
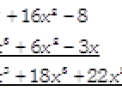Subtraction of Algebraic Expressions
Steps:
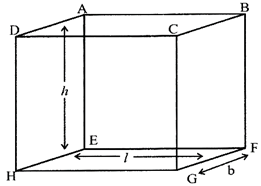Volume of the cuboid \[={{l}^{2}}\times b\times h\]
Diagonal of the cuboid \[=\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}\]
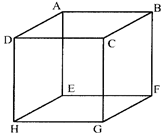If length of each edge of a cube is a.
Then, volume of the cube \[={{a}^{3}}\]
Total surface area of the cube \[=6{{a}^{2}}\]
Diagonal of the cube\[=\sqrt{3a}.\]
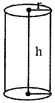Volume of the cylinder \[=\pi {{r}^{2}}h\]
Area of more...
