 Land preparation and cultivation methodology is among the basic factors which affect the yield of crops. For getting better yield, it is important to prepare land thoroughly, so that the weeds are destroyed and water absorption capacity of the soil is increased.
Crops
When the same kind of plants are grown in the fields on a large scale to obtain foods like cereals, pulses, vegetables and fruits, etc., it is called a crop.
Agriculture
The growing of plants (or crops) in the fields for obtaining food is called agriculture.
Crop production involves various agricultural practices such as:
Land preparation and cultivation methodology is among the basic factors which affect the yield of crops. For getting better yield, it is important to prepare land thoroughly, so that the weeds are destroyed and water absorption capacity of the soil is increased.
Crops
When the same kind of plants are grown in the fields on a large scale to obtain foods like cereals, pulses, vegetables and fruits, etc., it is called a crop.
Agriculture
The growing of plants (or crops) in the fields for obtaining food is called agriculture.
Crop production involves various agricultural practices such as:
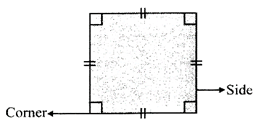 It has four sides and four comers. All its sides are of the same length.
(b) Rectangle.
It has four sides and four comers. All its sides are of the same length.
(b) Rectangle.
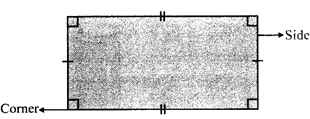 It has four sides and four comers. The opposite sides of a rectangle are parallel and of the same length. Every interior angle is a right \[\angle \]le.
(c) Triangle
It has four sides and four comers. The opposite sides of a rectangle are parallel and of the same length. Every interior angle is a right \[\angle \]le.
(c) Triangle
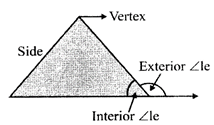 It has three sides and three vertices.
(d) Cuboid
It has three sides and three vertices.
(d) Cuboid
 It has 6 flat faces, 12 straight edges and 8 vertices.
(e) Cube
It has 6 flat faces, 12 straight edges and 8 vertices.
(e) Cube
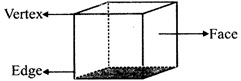 It has 6 flat faces, 8 vertices and 12 straight edges.
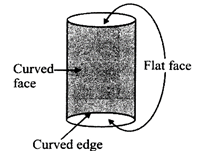
(f) Cylinder
It has 6 flat faces, 8 vertices and 12 straight edges.
(f) Cylinder
 more...
more...
You need to login to perform this action.
You will be redirected in
3 sec
