2. Current Affairs
  3. Current Affairs
  4. JEE Main & Advanced

Current Affairs JEE Main & Advanced

Equation of the Chord of the Parabola Which is Bisected at a Given Point  

The equation of the chord at the parabola \[{{y}^{2}}=4ax\] bisected at the point \[({{x}_{1}},{{y}_{1}})\] is given by \[T={{S}_{1,}}\]               i.e.,  \[y{{y}_{1}}-2a(x+{{x}_{1}})\]\[y{{y}_{1}}-2a(x+{{x}_{1}})=y_{1}^{2}-4a{{x}_{1}}\]     where \[T=y{{y}_{1}}-2a(x+{{x}_{1}})\] and \[{{S}_{1}}=y_{1}^{2}-4a{{x}_{1}}\].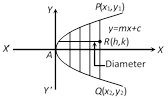  
Catgeory: JEE Main & Advanced

Equation of the Chord Joining any Two Points on the Parabola 

Let \[P(at_{1}^{2},2a{{t}_{1}}),Q(at_{2,}^{2},2a{{t}_{2}})\]be any two points on the parabola \[{{y}^{2}}=4ax\]. Then, the equation of the chord joining these points is, \[y-2a{{t}_{1}}=\frac{2}{{{t}_{1}}+{{t}_{2}}}\left( x-at_{1}^{2} \right)\] or \[y({{t}_{1}}+{{t}_{2}})=2x+2a{{t}_{1}}{{t}_{2}}\].     (1) Condition for the chord joining points having parameters \[{{\mathbf{t}}_{\mathbf{1}}}\] and \[{{\mathbf{t}}_{\mathbf{2}}}\] to be a focal chord: If the chord joining points \[(at_{1}^{2},2a{{t}_{1}})\] and \[(at_{2}^{2},2a{{t}_{2}})\] on the parabola passes through its focus, then \[(a,0)\] satisfies the equation \[y({{t}_{1}}+{{t}_{2}})=2x+2a{{t}_{1}}{{t}_{2}}\]     \[\Rightarrow \] \[0=2a+2a{{t}_{1}}{{t}_{2}}\] \[\Rightarrow \] \[{{t}_{1}}{{t}_{2}}=-1\] or \[{{t}_{2}}=-\frac{1}{{{t}_{1}}}\].     (2) Length of the focal chord: The length of a focal chord having parameters \[{{t}_{1}}\]and \[{{t}_{2}}\]for its end points is \[a{{({{t}_{2}}-{{t}_{1}})}^{2}}\].
Catgeory: JEE Main & Advanced

Diameter of a Parabola

The locus of the middle points of a system of parallel chords is called a diameter and in case of a parabola this diameter is shown to be a straight line which is parallel to the axis of the parabola.             The equation of the diameter bisecting chords of the parabola \[{{y}^{2}}=4ax\]of slope \[m\] is \[y=2a/m\].  
Catgeory: JEE Main & Advanced

Length of Tangent, Subtangent, Normal, Subnormal

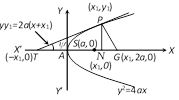Let the parabola \[{{y}^{2}}=4ax\]. Let the tangent and normal at \[P({{x}_{1}},{{y}_{1}})\] meet the axis of parabola at T and G respectively, and tangent at \[P({{x}_{1}},{{y}_{1}})\] makes angle \[\psi \] with the positive direction of x-axis. \[A(0,\,0)\] is the vertex of the parabola and \[PN=y\]. Then,           (1) Length of tangent \[=PT=PN\,\text{cosec}\,\,\psi ={{y}_{1}}\,\text{cosec}\,\psi \]   (2) Length of normal \[=PG=PN\text{cosec}({{90}^{o}}-\psi )={{y}_{1}}\sec \psi \]   (3) Length of subtangent \[=TN=PN\cot \psi ={{y}_{1}}\cot \psi \]   (4) Length of subnormal \[=NG=PN\cot ({{90}^{o}}-\psi )={{y}_{1}}\tan \psi \]   where, \[\tan \psi =\frac{2a}{{{y}_{1}}}=m\],  [Slope of tangent at \[P(x,\,\,y)\]]  
Catgeory: JEE Main & Advanced

Length of Tangent, Subtangent, Normal and Subnormal to \[{{\mathbf{y}}^{\mathbf{2}}}\mathbf{= 4ax}\,\,\mathbf{at }\,\mathbf{(a}{{\mathbf{t}}^{\mathbf{2}}}\mathbf{,2at)}\]

(1) Length of tangent at \[(a{{t}^{2}},2at)\]\[=2at\,\text{cosec}\psi \]      \[=2at\sqrt{(1+{{\cot }^{2}}\psi )}\] \[=2at\sqrt{1+{{t}^{2}}}\]     (2) Length of normal at \[(a{{t}^{2}},\,2at)=2at\sec \psi \]     \[=2at\sqrt{(1+{{\tan }^{2}}\psi )}\]\[=2a\sqrt{{{t}^{2}}+{{t}^{2}}{{\tan }^{2}}\psi }\] \[=2a\sqrt{({{t}^{2}}+1)}\]     (3) Length of subtangent at \[(a{{t}^{2}},2at)=2at\cot \psi \]\[=2a{{t}^{2}}\]     (4) Length of subnormal at \[(a{{t}^{2}},2at)=2at\tan \psi \]\[=2a\].
Catgeory: JEE Main & Advanced

Pole and Polar

The locus of the point of intersection of the tangents to the parabola at the ends of a chord drawn from a fixed point P is called the polar of point P and the point P is called the pole of the polar.   Equation of polar : Equation of polar of the point \[({{x}_{1}},\,{{y}_{1}})\] with respect to parabola \[{{y}^{2}}=4ax\] is same as chord of contact and is given by \[y{{y}_{1}}=2a(x+{{x}_{1}})\].          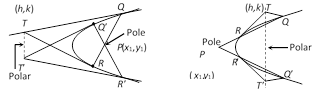Coordinates of pole : The pole of the line \[lx+my+n=0\] with respect to the parabola \[{{y}^{2}}=4ax\]is \[\left( \frac{n}{l},\frac{-2am}{l} \right)\].  
Catgeory: JEE Main & Advanced

Definition

An ellipse is the locus of a point which moves in such a way that its distance from a fixed point is in constant ratio \[(<1)\] to its distance from a fixed line. The fixed point is called the focus and fixed line is called the directrix and the constant ratio is called the eccentricity of the ellipse, denoted by (e).  
Catgeory: JEE Main & Advanced

Standard Equation of the Ellipse

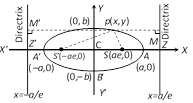Let S be the focus, ZM be the directrix of the ellipse and \[P(x,y)\]is any point on the ellipse, then by definition \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\], where \[{{b}^{2}}={{a}^{2}}(1-{{e}^{2}})\].   Since \[e<1\], therefore \[{{a}^{2}}(1-{{e}^{2}})<{{a}^{2}}\] Þ \[{{b}^{2}}<{{a}^{2}}\].            The other form of equation of ellipse is \[\frac{{{x}^{2}}}{{{y}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\], where, \[{{a}^{2}}={{b}^{2}}(1-{{e}^{2}})\,i.e.,\,a<b\]. 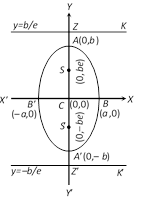        Difference between both ellipses will be clear from the following table :  
Ellipse   \[\left\{ \frac{{{x}^{\mathbf{2}}}}{{{a}^{\mathbf{2}}}}+\frac{{{y}^{\mathbf{2}}}}{{{b}^{\mathbf{2}}}}=\mathbf{1} \right\}\]
Imp. terms
  For \[\mathbf{a>b}\] For \[\mathbf{b>a}\]
Centre \[(0,\,\,0)\] \[(0,\,\,0)\]
Vertices \[(\pm a,\,0)\] \[(0,\,\pm b)\]
Length of major axis \[2a\] \[2b\]
Length of minor axis \[2b\] more...
Catgeory: JEE Main & Advanced

Parametric Form of The Ellipse

Let the equation of ellipse in standard form will be given by \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\].    Then the equation of ellipse in the parametric form will be given by \[x=a\cos \varphi ,y=b\sin \varphi \], where \[\varphi \] is the eccentric angle whose value vary from \[0\le \varphi <2\pi \]. Therefore coordinate of any point P on the ellipse will be given by \[(a\cos \varphi \,,\,b\sin \varphi )\].
Catgeory: JEE Main & Advanced

Special Forms of an Ellipse

(1) If the centre of the ellipse is at point \[(h,k)\] and the directions of the axes are parallel to the coordinate axes, then its equation is \[\frac{{{(x-h)}^{2}}}{{{a}^{2}}}+\frac{{{(y-k)}^{2}}}{{{b}^{2}}}=1\].     (2) If the equation of the curve is \[\frac{{{(lx+my+n)}^{2}}}{{{a}^{2}}}\] \[+\frac{{{(mx-ly+p)}^{2}}}{{{b}^{2}}}=1\], where \[lx+my+n=0\] and \[mx-ly+p=0\] are perpendicular lines, then we substitute \[\frac{lx+my+n}{\sqrt{{{l}^{2}}+{{m}^{2}}}}=X,\] \[\frac{mx-ly+p}{\sqrt{{{l}^{2}}+{{m}^{2}}}}=Y\], to put the equation in the standard form.
Catgeory: JEE Main & Advanced

Current Affairs Categories


Archive


Trending Current Affairs

You need to login to perform this action.
You will be redirected in 3 sec spinner