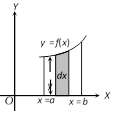
(2) If the curve \[y=f(x)\] lies below x-axis, then the area bounded by the curve \[y=f(x),\] the x-axis and the ordinates \[x=a\] and \[x=b\] is negative. So, area is given by \[\left| \int_{a}^{b}{y\,dx} \right|\].
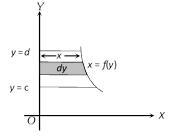
(3) The area bounded by a cartesian curve\[x=f(y),\,\] y-axis and abscissae \[y=c\] and \[y=d\] is given by,
Area \[=\int_{c}^{d}{x\,dy=\int_{c}^{d}{f(y)dy}}\]
(4) If the equation of a curve is in parametric form, let \[x=f(t),\,\,y=g(t)\] then the area \[=\int_{a}^{b}{y\,dx}=\int_{{{t}_{1}}}^{{{t}_{2}}}{g(t)\,f'(t)\,dt}\] , where \[{{t}_{1}}\] and \[{{t}_{2}}\] are the values of \[t\] respectively corresponding to the values of \[a\] and \[b\] of \[x\].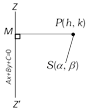 
\[SP=ePM\]\[\Rightarrow \] \[S{{P}^{2}}={{e}^{2}}P{{M}^{2}}\]
\[\Rightarrow \] \[{{(h-\alpha )}^{2}}+{{(k-\beta )}^{2}}={{e}^{2}}{{\left( \frac{Ah+Bk+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right)}^{2}}\]
Thus the locus of \[(h,k)\] is \[{{(x-\alpha )}^{2}}+{{(y-\beta )}^{2}}=\]\[{{e}^{2}}\frac{{{(Ax+By+C)}^{2}}}{({{A}^{2}}+{{}^{2}})}\]
which is general equation of second degree. | S. No. | Condition | Nature of conic |
| 1. | \[\Delta =0\] and \[ab-{{h}^{2}}=0\grave{\ }\] | A pair of coincident straight lines |
| 2. | \[\Delta =0\] and \[ab-{{h}^{2}}<0\] | A pair of intersecting straight lines |
| 3. | \[\Delta =0\] and \[ab-{{h}^{2}}>0\] | A point |
| S. No. | Condition | Nature of conic |
| 1. | \[\Delta \ne 0,\,\,h=0,\,\,a=b,\,\,e=0\] | A circle | more...
If the vertex of the parabola is \[(p,\,q)\] and its axis is parallel to y-axis, then the equation of the parabola is \[{{(x-p)}^{2}}=4b(y-q)\]. 
