| Parabola | \[{{y}^{2}}=4ax\] | \[{{y}^{2}}=-4ax\] | \[{{x}^{2}}=4ay\] | \[{{x}^{2}}=-4ay\] |
| Parametric Co-ordinates | \[(a{{t}^{2}},2at)\] | \[(-a{{t}^{2}},2at)\] | \[(2at,a{{t}^{2}})\] | \[(2at,\ -a{{t}^{2}})\] |
| Parametric Equations | \[x=a{{t}^{2}}\] \[y=2at\] | \[x=-a{{t}^{2}}\] \[y=2at\] | \[x=2at\] \[y=a{{t}^{2}}\] | \[x=2at\], \[y=-a{{t}^{2}}\] |
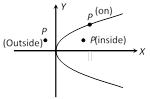(2) Intersection of a line and a parabola: The line \[y=mx+c\] does not intersect, touches or intersect a parabola \[{{y}^{2}}=4ax\], according as \[c>,=,<\frac{a}{m}\].
Condition of tangency : The line \[y=mx+c\] touches the parabola, if \[c=a/m\]. | Equations of tangent of all other standard parabolas at \[\mathbf{(}{{\mathbf{x}}_{\mathbf{1}}}\mathbf{,}{{\mathbf{y}}_{\mathbf{1}}}\mathbf{)}\] | |
| Equation of parabola | Tangent at \[\mathbf{(}{{\mathbf{x}}_{\mathbf{1}}}\mathbf{,}{{\mathbf{y}}_{\mathbf{1}}}\mathbf{)}\] |
| \[{{y}^{2}}=4ax\] | \[y{{y}_{1}}=\text{ }2a(x+{{x}_{1}})\] |
| \[{{y}^{2}}=-4ax\] | \[y{{y}_{1}}=-2a(x+{{x}_{1}})\] |
| \[{{x}^{2}}=4ay\] | \[x{{x}_{1}}=2a(y+{{y}_{1}})\] |
| \[{{x}^{2}}=-4ay\] | \[x{{x}_{1}}=-2a(y+{{y}_{1}})\] |
| Equations of tangent of all other standard parabolas at \[\mathbf{'t'}\] | |||||||||||||||||||||||||
| Equations of parabolas | Parametric co-ordinates \[\mathbf{'t'}\] | Tangent at \[\mathbf{'t'}\] | |||||||||||||||||||||||
| \[{{y}^{2}}=4ax\] | \[(a{{t}^{2}},2at)\] | \[ty=x+a{{t}^{2}}\] | |||||||||||||||||||||||
| \[{{y}^{2}}=-4ax\] | \[(-a{{t}^{2}},2at)\] | more...
(1) The point of intersection of tangents at two points \[P(at_{1}^{2},2a{{t}_{1}})\] and \[Q(at_{2}^{2},2a{{t}_{2}})\] on the parabola \[{{y}^{2}}=4ax\] is \[(a{{t}_{1}}{{t}_{2}},a({{t}_{1}}+{{t}_{2}}))\].
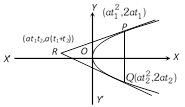(2) The locus of the point of intersection of tangents to the parabola \[{{y}^{2}}=4ax\] which meet at an angle \[\alpha \] is \[{{(x+a)}^{2}}{{\tan }^{2}}\alpha ={{y}^{2}}-4ax\].
(3) Director circle: The locus of the point of intersection of perpendicular tangents to a conic is known as its director circle. The director circle of a parabola is its directrix.
(4) The tangents to the parabola \[\frac{x{{x}_{1}}}{{{a}^{2}}}-\frac{y{{y}_{1}}}{{{b}^{2}}}=1\] at \[P(at_{1}^{2},2a{{t}_{1}})\] and \[Q(at_{2}^{2},2a{{t}_{2}})\] intersect at R. Then the area of triangle \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is \[\frac{1}{2}{{a}^{2}}{{({{t}_{1}}-{{t}_{2}})}^{3}}\].
The combined equation of the pair of the tangents drawn from a point to a parabola is \[SS'={{T}^{2}}\], where \[S={{y}^{2}}-4ax;\] \[S'=y_{1}^{2}-4a{{x}_{1}}\] and \[T=y{{y}_{1}}-2a(x+{{x}_{1}})\].
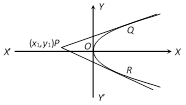The two tangents can be drawn from a point to a parabola. The two tangent are real and distinct or coincident or imaginary according as the given point lies outside, on or inside the parabola.
(1) Point form
| |||||||||||||||||||||||
then \[{{t}_{2}}=-{{t}_{1}}-\frac{2}{{{t}_{1}}}\]. 
Properties of co-normal points
(1) Three normals can be drawn from a point to a parabola.
(2) The algebraic sum of the slopes of three concurrent normals is zero.
(3) The sum of the ordinates of the co-normal points is zero.
(4) The centroid of the triangle formed by the co-normal points lies on the axis of the parabola.
(5) The centroid of a triangle formed by joining the foots of the normal of the parabola lies on its axis and is given by
\[\left( \frac{am_{1}^{2}+am_{2}^{2}+am_{3}^{2}}{3},\frac{2a{{m}_{1}}+2a{{m}_{2}}+2a{{m}_{3}}}{3} \right)\]\[=\left( \frac{am_{1}^{2}+am_{2}^{2}+am_{3}^{2}}{3},0 \right)\].
(6) If three normals drawn to any parabola \[{{y}^{2}}=4ax\]from a given point (h, k) be real, then \[h>2a\] for \[a=1\], normals drawn to the parabola \[{{y}^{2}}=4x\] from any point (h, k) are real, if \[h>2\].
(7) Out of these three at least one is real, as imaginary normals will always occur in pairs. 
The chord of contact of tangents drawn from a point \[({{x}_{1}},{{y}_{1}})\] to the parabola \[{{y}^{2}}=4ax\] is \[y{{y}_{1}}=2a(x+{{x}_{1}})\]. 
