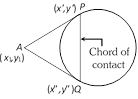
 (2) Equation of chord of contact : The equation of the chord of contact of tangents drawn from a point \[({{x}_{1}},\,{{y}_{1}})\] to the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}.\]
Equation of chord of contact at \[({{x}_{1}},\,{{y}_{1}})\] to the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] is \[x{{x}_{1}}+y{{y}_{1}}+g(x+{{x}_{1}})+f(y+{{y}_{1}})+c=0\].
It is clear from above that the equation to the chord of contact coincides with the equation of the tangent, if point \[({{x}_{1}},\,{{y}_{1}})\] lies on the circle.
The length of chord of contact \[=2\sqrt{{{r}^{2}}-{{p}^{2}}}\]; (p being length of perpendicular from centre to the chord)
Area of \[\Delta APQ\] is given by \[\frac{a{{(x_{1}^{2}+y_{1}^{2}-{{a}^{2}})}^{3/2}}}{x_{1}^{2}+y_{1}^{2}}\].
(3) Equation of the chord bisected at a given point : The equation of the chord of the circle \[S\equiv {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] bisected at the point \[({{x}_{1}},\,{{y}_{1}})\] is given by \[T={{S}_{1}}\].
i.e., \[x{{x}_{1}}+y{{y}_{1}}+g(x+{{x}_{1}})+f(y+{{y}_{1}})+c=x_{1}^{2}+y_{1}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+c\].
(2) Equation of chord of contact : The equation of the chord of contact of tangents drawn from a point \[({{x}_{1}},\,{{y}_{1}})\] to the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}.\]
Equation of chord of contact at \[({{x}_{1}},\,{{y}_{1}})\] to the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] is \[x{{x}_{1}}+y{{y}_{1}}+g(x+{{x}_{1}})+f(y+{{y}_{1}})+c=0\].
It is clear from above that the equation to the chord of contact coincides with the equation of the tangent, if point \[({{x}_{1}},\,{{y}_{1}})\] lies on the circle.
The length of chord of contact \[=2\sqrt{{{r}^{2}}-{{p}^{2}}}\]; (p being length of perpendicular from centre to the chord)
Area of \[\Delta APQ\] is given by \[\frac{a{{(x_{1}^{2}+y_{1}^{2}-{{a}^{2}})}^{3/2}}}{x_{1}^{2}+y_{1}^{2}}\].
(3) Equation of the chord bisected at a given point : The equation of the chord of the circle \[S\equiv {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] bisected at the point \[({{x}_{1}},\,{{y}_{1}})\] is given by \[T={{S}_{1}}\].
i.e., \[x{{x}_{1}}+y{{y}_{1}}+g(x+{{x}_{1}})+f(y+{{y}_{1}})+c=x_{1}^{2}+y_{1}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+c\].  (1) Equation of normal: The equation of normal to the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] at any point \[({{x}_{1}},\,{{y}_{1}})\] is \[y-{{y}_{1}}=\frac{{{y}_{1}}+f}{{{x}_{1}}+g}(x-{{x}_{1}})\] or \[\frac{x-{{x}_{1}}}{{{x}_{1}}+g}=\frac{y-{{y}_{1}}}{{{y}_{1}}+f}\].
The equation of normal to the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] at any point \[a{{x}^{2}}+2hxy+b{{y}^{2}}\] is \[x{{y}_{1}}-{{x}_{1}}y=0\] or \[\frac{x}{{{x}_{1}}}=\frac{y}{{{y}_{1}}}\].
(2) Parametric form : Since parametric co-ordinates of a point on the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[+2gx+2fy+c=0\].
\[\therefore \] Equation of normal at\[(a\,\,\cos \theta ,\,\,\,a\,\,\sin \theta )\] is \[\frac{x}{a\,\cos \theta }=\frac{y}{a\,\sin \,\theta }\]
or \[\frac{x}{\cos \theta }=\frac{y}{\sin \,\theta }\] or \[y=x\,\,\tan \,\theta \] or \[y=mx\] where \[m=\tan \,\,\theta \], which is slope form of normal.
(1) Equation of normal: The equation of normal to the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] at any point \[({{x}_{1}},\,{{y}_{1}})\] is \[y-{{y}_{1}}=\frac{{{y}_{1}}+f}{{{x}_{1}}+g}(x-{{x}_{1}})\] or \[\frac{x-{{x}_{1}}}{{{x}_{1}}+g}=\frac{y-{{y}_{1}}}{{{y}_{1}}+f}\].
The equation of normal to the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] at any point \[a{{x}^{2}}+2hxy+b{{y}^{2}}\] is \[x{{y}_{1}}-{{x}_{1}}y=0\] or \[\frac{x}{{{x}_{1}}}=\frac{y}{{{y}_{1}}}\].
(2) Parametric form : Since parametric co-ordinates of a point on the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[+2gx+2fy+c=0\].
\[\therefore \] Equation of normal at\[(a\,\,\cos \theta ,\,\,\,a\,\,\sin \theta )\] is \[\frac{x}{a\,\cos \theta }=\frac{y}{a\,\sin \,\theta }\]
or \[\frac{x}{\cos \theta }=\frac{y}{\sin \,\theta }\] or \[y=x\,\,\tan \,\theta \] or \[y=mx\] where \[m=\tan \,\,\theta \], which is slope form of normal. 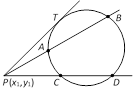 \[x_{1}^{2}+y_{1}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+c={{S}_{1}}\]
\[\therefore \,\,\,\,PA\,.\,PB={{(\sqrt{{{S}_{1}}})}^{2}}=\]
Square of the length of tangent.
If P is outside, inside or on the circle then PA. PB is \[+ve\], \[-ve\] or zero respectively.
\[x_{1}^{2}+y_{1}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+c={{S}_{1}}\]
\[\therefore \,\,\,\,PA\,.\,PB={{(\sqrt{{{S}_{1}}})}^{2}}=\]
Square of the length of tangent.
If P is outside, inside or on the circle then PA. PB is \[+ve\], \[-ve\] or zero respectively.  Let the circle be \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\], then equation of director circle is \[{{x}^{2}}+{{y}^{2}}=2{{a}^{2}}\].
Obviously director circle is a concentric circle whose radius is \[\sqrt{2}\] times the radius of the given circle.
Director circle of circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] is \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+2c-{{g}^{2}}-{{f}^{2}}=0\].
Let the circle be \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\], then equation of director circle is \[{{x}^{2}}+{{y}^{2}}=2{{a}^{2}}\].
Obviously director circle is a concentric circle whose radius is \[\sqrt{2}\] times the radius of the given circle.
Director circle of circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] is \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+2c-{{g}^{2}}-{{f}^{2}}=0\].
 where \[S=0\] is the equation of circle, \[T=0\] is the equation of tangent at \[({{x}_{1}},\,{{y}_{1}})\] and \[{{S}_{1}}\] is obtained by replacing \[x\] by \[{{x}_{1}}\] and \[y\] by \[{{y}_{1}}\] in S.
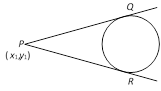
where \[S=0\] is the equation of circle, \[T=0\] is the equation of tangent at \[({{x}_{1}},\,{{y}_{1}})\] and \[{{S}_{1}}\] is obtained by replacing \[x\] by \[{{x}_{1}}\] and \[y\] by \[{{y}_{1}}\] in S. 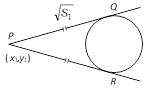 Then \[PQ=PR\] is called the length of tangent drawn from point \[P\] and is given by \[PQ=PR\] \[=\sqrt{x_{1}^{2}+y_{1}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+c}=\sqrt{{{S}_{1}}}\].
Then \[PQ=PR\] is called the length of tangent drawn from point \[P\] and is given by \[PQ=PR\] \[=\sqrt{x_{1}^{2}+y_{1}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+c}=\sqrt{{{S}_{1}}}\].  (i) The equation of tangent at \[({{x}_{1}},{{y}_{1}})\] to circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}\].
(ii) The equation of tangent at \[({{x}_{1}},{{y}_{1}})\] to circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]is\[x{{x}_{1}}+y{{y}_{1}}+g(x+{{x}_{1}})+f(y+{{y}_{1}})+c=0\].
(2) Parametric form : Since parametric co-ordinates of a point on the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[(a\,\cos \theta ,\,a\,\sin \theta ),\] then equation of tangent at \[(a\,\cos \theta ,\,a\,\sin \theta )\] is \[x.\,a\,\cos \theta +y\,.\,a\,\sin \theta ={{a}^{2}}\]
or \[x\,\cos \theta +y\,\sin \theta =a\].
(3) Slope form : The straight line \[y=mx+c\] touches the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] if \[{{c}^{2}}={{a}^{2}}(1+{{m}^{2}})\] and the point of contact of tangent \[y=mx\pm a\sqrt{1+{{m}^{2}}}\] is \[\left( \frac{\mp ma}{\sqrt{1+{{m}^{2}}}},\,\,\frac{\pm a}{\sqrt{1+{{m}^{2}}}} \right)\].
(i) The equation of tangent at \[({{x}_{1}},{{y}_{1}})\] to circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}\].
(ii) The equation of tangent at \[({{x}_{1}},{{y}_{1}})\] to circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]is\[x{{x}_{1}}+y{{y}_{1}}+g(x+{{x}_{1}})+f(y+{{y}_{1}})+c=0\].
(2) Parametric form : Since parametric co-ordinates of a point on the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[(a\,\cos \theta ,\,a\,\sin \theta ),\] then equation of tangent at \[(a\,\cos \theta ,\,a\,\sin \theta )\] is \[x.\,a\,\cos \theta +y\,.\,a\,\sin \theta ={{a}^{2}}\]
or \[x\,\cos \theta +y\,\sin \theta =a\].
(3) Slope form : The straight line \[y=mx+c\] touches the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] if \[{{c}^{2}}={{a}^{2}}(1+{{m}^{2}})\] and the point of contact of tangent \[y=mx\pm a\sqrt{1+{{m}^{2}}}\] is \[\left( \frac{\mp ma}{\sqrt{1+{{m}^{2}}}},\,\,\frac{\pm a}{\sqrt{1+{{m}^{2}}}} \right)\]. 
You need to login to perform this action.
You will be redirected in
3 sec
