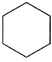
Solution:
There are 6 line segments in the given figure.
Ray
It is defined as the extension of a line segment in one direction up to infinity.
Solution: There are 12 rays.
Line
Line is defined as the extension of a line segment up to infinite in either direction.
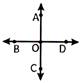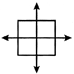Solution: There are two lines.
Angle
Inclination between two rays having common end point is called angle.
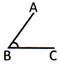\[\angle ABC\] is a angle
A Right Angle
An angle whose measure is exactly \[90{}^\circ \]is a right angle.
\[\angle ABC\]is a right angle
An Acute Angle
An angle whose measure is less than \[90{}^\circ \]is an acute angle.
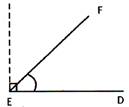\[\angle DEF\]is an acute angle.
An Obtuse Angle
An angle whose measure is greater than \[90{}^\circ \] but less than \[180{}^\circ \]is an obtuse angle.
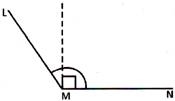\[\angle LMN\]is an obtuse angle
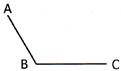Solution: It is an obtuse angle, because its measure is greater than\[90{}^\circ \].
Polygon
A Simple closed figure formed of three or more line segments is called a polygon. Line segments which form a polygon are called its sides. The point at which two adjacent sides of a polygon meet, is called a vertex of polygon. In the given figure, triangle, quadrilateral, pentagon and hexagon, all are examples of polygon.
Types of Polygons
Regular and Irregular Polygon
A regular polygon has all sides equal and all angles equal, more...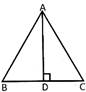 
Area of a Triangle
Area of a triangle \[=\frac{1}{2}\times Base\times Height\]
Where base is one side of a triangle and height is the length of altitude drawn from opposite vertex on the given base.
Area of the triangle ABC\[=\frac{1}{2}\times AD\times BC\]
Where BC is the base and AD is the height.
Area of the rectangle ABCD =\[=AB\times BC\]
Area of the square ABCD\[=AB\times AB\]
Perimetre of the Triangles
Perimetre of a triangle = Sum of length of all three sides.
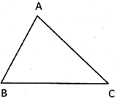Perimetre of the triangle \[ABC=AB+BC+CA\]
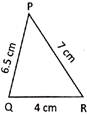Solution: Perimetre of the figure
\[=6.5\text{ }cm+7\text{ }cm+4\text{ }cm=17.5\text{ }cm\]
Perimetre of a Quadrilateral
The perimetre of a quadrilateral = Sum of the length of all four sides.
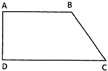Perimetre of the quadrilateral ABCD
\[=AB+BC+CD+DA\]
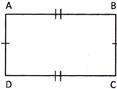Perimetre of the rectangle ABCD \[=2\,\,(AB+BC)\]
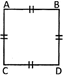Perimetre of the square ABCD \[=4\times AB\] more... | Australia |
|
| Pakistan |
|
| South Africa |
|
| Newzealand |
|
| England |
|
represents one six.
(a) Against which country Sehwag more... 
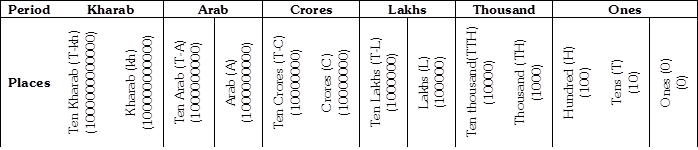
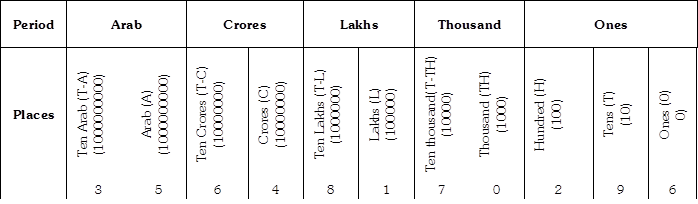Solution:
Thirty five Arab sixty four crore eighty one lakh seventy thousand two hundred ninety six.
International System of Numeration
This system of numeration is widely used in the most part of the world.
Given below is the place value chart of international system
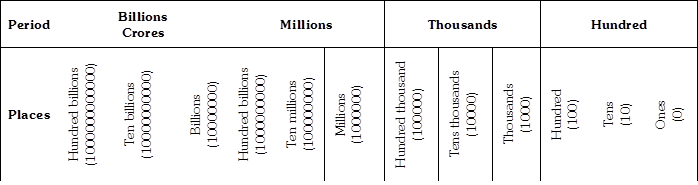In this system of numeration, as shown in the chart, every period has three groups.
The digits under each group are read together with the period.
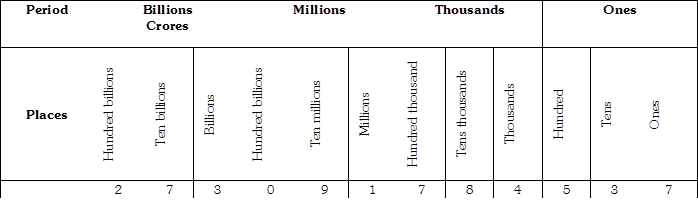Solution:
Two hundred seventy three billions ninety one million seven hundred eighty four thousand five hundred thirty seven.
Face Value of a Digit in Numerals
The face value of the digit in the numeral is the value of the digit itself.
For example, the face value of 5 in the numeral 5234698230 is 5 itself.
Place value
When we multiply the face value of the digit with the value of period, it gives place value.
For example, in the numeral 7854698230 the place value of 7 is \[(7\times 1000000000),\]that is, 7000000000.
Expanded From
Expanded form means expansion of any number according to the place value of the digits.
For example
\[7894564122=7\times 1000000000+8\times 100000000\]\[+9\times 10000000+4\times 1000000+5\times 100000\]
\[+6\times 10000+4\times 1000+1\times 100+2\times 10+2\times 1\].
Successor
It is defined as a number which is one more than the given number.
For example, the successor of 5498785245685623 is 5498785245685624
Predecessor
It is defined as a number which is one less than the given number.
For example, the predecessor of 9891436357895 is 9891436357894
| Roman Numeral | Hindu-Arabic Numeral |
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | more...
Operation on Numbers Addition and Subtraction
Introduction
In our daily life, we come across many activities when we need to apply the method of addition and subtraction. We are aware of numbers and number system. Now we will discuss two simple algebraic operations, that is, addition and subtraction.
Addition
Addition is one of the very common arithmetic operation used in mathematics. Addition is the operation to know the total quantity, when two or more than two quantities are taken together.
Operation on Numbers Multiplication and Division
Introduction
In this chapter we will study two important arithmetic operations "multiplication and division". Multiplication is repeated addition of a specific quantity, whereas division is a distribution of a quantity into some equal parts. Let us study them.
Multiplication
When a quantity is added to itself for a number of times, we use operation of multiplication to find the resulting quantity.
Multiplication of Two Natural Number
Place the multiplicands and multipliers of multiplicands with the first number multiplication by second number of the line in column, leaving the first place the products, the result is your answer
Look at the example below:
Example
Find the product of 24 and 15
\[24\times 15=360\]
Solution:
Word Problems Based on Multiplication
Distance covered by the aeroplane 
Note:
The product of two natural numbers is always a natural number.
Division
Division is the distribution of a quantity into some equal parts in such a way that each part contains equal amount.
Factors and Multiples
Factors of a Number
All the numbers, which divide a certain number exactly, without leaving a remainder are called factors of that number.
For example:
\[\Rightarrow \]1, 2, 3, 4, 6 and 12 are factors of 12.
Note: Factors of a number always include 1 and the number itself.
\[\Rightarrow \]1, 3, 5 and 15 are factors of 15.
Fractions and Decimals
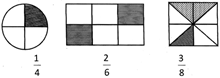
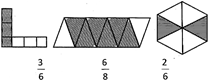
Fraction
Fraction is used to indicate a part of a whole. Fraction is written as\[\frac{a}{b}\].
The top number in a fraction is called numerator and the bottom number is called denominator of the fraction. Hence in the given example 'a' is numerator and 'b' is denominator. Look at the shaded part in the following figures which has been represented by fractions:
Unitary Method
Unitary Method
Unitary method is a method under which a calculation is carried out to find the value of the number of items, by first finding the value of one item.
From daily life experience, we know that when we increase the quantity of articles, their cost increases and when we decrease the quantity of articles, their cost decreases. In other words, more articles have more value and less articles have less value.
Note: In unitary method:
(i) To get more value we multiply.
(ii) To get less value we divide.
To solve the problems by unitary method we follow two steps:
Step 1: Get the value of a single unit.
Step 2: Then find the value of required units.
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |
