\[\therefore \] Common multiples of 2 and 4 are 4, 8, 12, ......
| Note: if the numerator is equal to the denominator, the fraction represents a whole number, i.e., 1 |
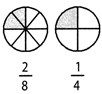Both \[\frac{2}{8}\] and \[\frac{1}{4}\] represent the same part of a whole. So \[\frac{2}{8}=\frac{1}{4}\].
Comparing fractions:
(a) Fractions with the same numerators: Of two fractions with a common numerator, the fraction that has a smaller denominator is greater.
e.g., \[\frac{3}{5}\]and \[\frac{3}{7}\]
Since, the numerators are the same, comparing their denominators, we get \[\text{5}<\text{7}\].
\[\therefore \] \[\frac{3}{5}>\frac{3}{7}\]
(b) Fractions with the same denominators: Of two fractions with a common denominator, the fraction that has a larger numerator is greater
e.g., \[\frac{2}{9}\]and \[\frac{7}{9}\]
Since the denominators are the same, comparing their numerators, we get \[7>2\].
\[\therefore \] \[\frac{7}{9}>\frac{2}{9}\]
(c) Fractions with different numerators and denominators: To compare fractions with different numerators and denominators, first convert them to get the same denominator by writing their equivalent fractions and then compare.
e.g., \[\frac{3}{4}\] and \[\frac{5}{6}\]
Step 1: Check if numerators or denominators are the same. The given fractions do not have the same numerators or denominators.
Step 2: Find equivalent fractions with common denominators. \[\frac{3\times 3}{4\times 3}=\frac{9}{12}\] and \[\frac{5\times 2}{6\times 2}=\frac{10}{12}\]
Step 3: Compare more... | Period | Kharab | Arab | Crores | Lakhs | Thousands | Ones | ||||||
| Places | ten Kharab (T-kh) 1000000000000 | Kharab (kh) 00000000000 | Ten Arab (T-A) 1000000000 | Arab (A) 100000000 | Ten Crores (T-C) 10000000 | Crores (C) 1000000 | Ten lakhs (T-L) 100000 | Lakhs (L) 10000 | Ten thousands (T-TH) 10000 | Thousands (TH) 1000 | Hundred (H) 100 | Ones (0) 0 |
| Period | Arab | Crores | Lakhs | Thousands | Ones | |||||||||||||
| Places | Ten Arab (T-A) (10000000000) | more...
Roman Numerals
Introduction
The numerals we use is commonly known as Indo-Arabic Numerals. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ______ etc., are example of indo -Arabic numerals in ancient time Romans developed a system of numerations (numbering) which is known as Roman Numerals. I, II, III, IV, V, VI, VII, VIII, IX, _______ etc. are example of Roman Numerals.
Roman numerals are formed by using the following symbols:
Operation on Numbers: Addition and Subtraction
Introduction
In our daily life, we come across many activities when we need to apply the method of addition and subtraction. We are aware of numbers and number system. Now we will discuss two simple algebraic operations, that is, addition and subtraction.
Addition
Addition is one of the very common arithmetic operation used in mathematics. Addition is the operation to know the total quantity, when two or more than two quantities are taken together.
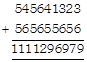Terms related to addition
(i) Addends: The numbers which are added to each other are called addends.
(ii) Sum: The result of the addition is called sum.
Look at the example given below.
\[\begin{align}
& \,\,\,\,766061\to First\,addend \\
& \underline{+\,586505}\to Second\,addend \\
& \underline{1352566\to }\,Sum \\
\end{align}\]
Operation on Numbers - Multiplication and Division
Introduction
In this chapter we will study two important arithmetic operations "multiplication and division". Multiplication is repeated addition of a specific quantity, whereas division is a distribution of a quantity into some equal parts. Let us study them.
Multiplication
When a quantity is added to itself for a number of times, we use operation of multiplication to find the resulting quantity,
Multiplication of a Number by Power of 10
When a number is multiplied by power of 10, the number of 0 is added to the right to the number, as the number of zeroes in the power of 10.
Fractions and Decimals
Fraction
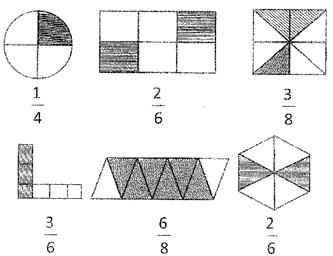
Fraction is used to indicate a part of a whole. Fraction is written, for example, as\[\frac{a}{b}\]. The top number in a fraction is called numerator and the bottom number is called denominator of the fraction. Hence in the given example 'a' is numerator and 'b' is denominator.
Look at the shaded part in the following figures which has been represented by fractions:
Unitary Method
Unitary Method
Unitary method is a method under which a calculation is carried out to find the value of the number of items, by first finding the value of one item.
From daily life experience, we know that when we increase the quantity of articles, their cost increases and when we decrease the quantity of articles, their cost decreases. In other words, more articles have more value and less articles have less value.
Note: In unitary method:
(i) To get more value we multiply.
(ii) To get less value we divide.
Money
Introduction
We require a number of things in our day to day life. We buy these things from the market and in return we pay money as per the rate of the article. So money is of great importance to us.
Different countries use different currencies. Indian currency is known as rupees.
Short form of the rupees is Rs, written by the symbol Rs. We write 78 rupees as Rs. 78.
Conversion of Rupees into Paise
One rupee is equal to 100 paise, so to convert rupees into paise, we multiply the Rs. by 100.
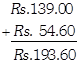Problems Based on Money
Problems based on money may be on addition, subtraction, multiplication and division.
Geometrical Figures
Introduction
In our day to day life we come across a number of objects. All the objects has a specific shape and size.
We recognize a number of objects by their shape. Therefore, to know about the objects and of their shapes is very important. In this chapter we will study about the shapes of different geometrical figures.
Point
To show a particular location, a dot (.) is placed over it, that dot is known as a point.
A is a point
Line Segment
Line segment is defined as the shortest distance between two fixed points. It has fixed length.
Solution:
There are 6 line segments in the given figure.
Ray
It is defined as the extension of a line segment in one direction up to infinity.
Solution:
There are 12 rays.
Line
Line is defined as the extension of a line segment up to infinite in either direction.
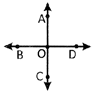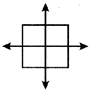Solution:
There are two lines.
Angle
Inclination between two rays having common end point is called angle.
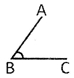\[\angle ABC\] is a angle
A Right Angle
An angle whose measure is exactly \[90{}^\circ \] is a right angle.
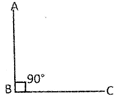\[\angle ABC\]is a right angle
An Acute Angle
An angle whose measure is less than \[90{}^\circ \] is an acute angle.
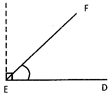\[\angle DEF\] is an acute more... Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. | ||||||||||||||||
