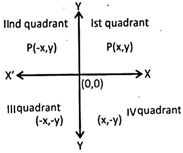
 x\[\to \] abscissa
y\[\to \] ordinate
x\[\to \] abscissa
y\[\to \] ordinate
 (b) Distance between the origin 0(0, 0) and the point P(x, y) is OP
\[op=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
e.g.\[A=(5,3)\,\,\,B=(-2,5)\]
\[\therefore \,\,\,AB\]
\[=\sqrt{{{(-2-5)}^{2}}{{(5-3)}^{2}}}=\sqrt{49+4}=\sqrt{53}\]
(b) Distance between the origin 0(0, 0) and the point P(x, y) is OP
\[op=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
e.g.\[A=(5,3)\,\,\,B=(-2,5)\]
\[\therefore \,\,\,AB\]
\[=\sqrt{{{(-2-5)}^{2}}{{(5-3)}^{2}}}=\sqrt{49+4}=\sqrt{53}\]
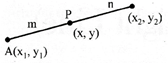 When P divides AB in the ratio m:n then
\[x=\frac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\] \[y=\frac{m{{y}_{2}}-n{{y}_{1}}}{m-n},\]
When P divides AB in the ratio 1:1 i.e. P is the mid point of AB
\[\therefore \,\,\,\text{P}\equiv \text{(x,y)=}\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{2}}+{{y}_{1}}}{2} \right)\]
When P divides AB in the ratio m:n then
\[x=\frac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\] \[y=\frac{m{{y}_{2}}-n{{y}_{1}}}{m-n},\]
When P divides AB in the ratio 1:1 i.e. P is the mid point of AB
\[\therefore \,\,\,\text{P}\equiv \text{(x,y)=}\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{2}}+{{y}_{1}}}{2} \right)\]
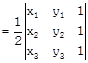 [Using determinant form]
[Using determinant form]
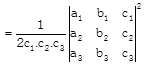 Where \[{{c}_{1}},\,{{c}_{2}},\,{{c}_{3}}\] be the co-factor of \[{{c}_{1}},\,{{c}_{2}},\,{{c}_{3}}\] in the determinants:
\[\therefore \,\,\,{{c}_{1}}={{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{2}},\]
\[{{c}_{2}}={{a}_{3}}.{{b}_{1}}-{{a}_{1}}{{b}_{3}}\]
& \[{{c}_{3}}={{a}_{1}}.{{b}_{2}}-{{a}_{2}}{{b}_{1}}.\]
Where \[{{c}_{1}},\,{{c}_{2}},\,{{c}_{3}}\] be the co-factor of \[{{c}_{1}},\,{{c}_{2}},\,{{c}_{3}}\] in the determinants:
\[\therefore \,\,\,{{c}_{1}}={{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{2}},\]
\[{{c}_{2}}={{a}_{3}}.{{b}_{1}}-{{a}_{1}}{{b}_{3}}\]
& \[{{c}_{3}}={{a}_{1}}.{{b}_{2}}-{{a}_{2}}{{b}_{1}}.\]
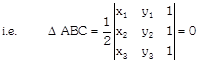 [In determinant form]
Solved Problem
[In determinant form]
Solved Problem
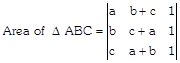
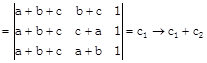
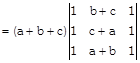 [Two columns are identical]
\[=(a+b+c)\times 0=0\]
Hence more...
[Two columns are identical]
\[=(a+b+c)\times 0=0\]
Hence more...  (a) If \[\Delta \ne 0\] & \[{{h}^{2}}-ab\ge 0\] then this general equation of second degree in x & y represents the equation of hyperbola.
(b) If \[\Delta \ne 0\] & \[{{h}^{2}}-ab\le 0\] then this pair of lines represent the equation ellipse.
(c) If \[\Delta \ne 0\] & \[{{h}^{2}}-ab=0\] then this pair of lines represent the equation of parabola
(d) If \[a=b=1\] & \[h=0\] then this represents the equation of circle.
(a) If \[\Delta \ne 0\] & \[{{h}^{2}}-ab\ge 0\] then this general equation of second degree in x & y represents the equation of hyperbola.
(b) If \[\Delta \ne 0\] & \[{{h}^{2}}-ab\le 0\] then this pair of lines represent the equation ellipse.
(c) If \[\Delta \ne 0\] & \[{{h}^{2}}-ab=0\] then this pair of lines represent the equation of parabola
(d) If \[a=b=1\] & \[h=0\] then this represents the equation of circle.
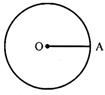 Let C (O, r) is a circle with centre 0 & radius r. A be any point it.
\[\therefore \] OA = radius of the circle
Let C (O, r) is a circle with centre 0 & radius r. A be any point it.
\[\therefore \] OA = radius of the circle
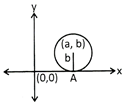 \[{{({{x}^{2}}-a)}^{2}}+{{(y-b)}^{2}}={{b}^{2}}\]
\[{{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}+{{b}^{2}}={{b}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}=0\]
(ii) Circle with centre, (a, b) which touches the y-axis.
Since, equation of the circle touches the y- axis. i.e. the radius of the circle is equao to the x- ordinate of the centre of the circle.
i.e. Radius of the circle is
\[{{({{x}^{2}}+a)}^{2}}+{{(y-b)}^{2}}={{a}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}+{{b}^{2}}={{a}^{2}}\]
\[{{({{x}^{2}}-a)}^{2}}+{{(y-b)}^{2}}={{b}^{2}}\]
\[{{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}+{{b}^{2}}={{b}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}=0\]
(ii) Circle with centre, (a, b) which touches the y-axis.
Since, equation of the circle touches the y- axis. i.e. the radius of the circle is equao to the x- ordinate of the centre of the circle.
i.e. Radius of the circle is
\[{{({{x}^{2}}+a)}^{2}}+{{(y-b)}^{2}}={{a}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}+{{b}^{2}}={{a}^{2}}\]
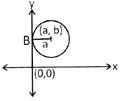 \[{{x}_{2}}+{{y}_{2}}-2ax-2by+{{b}_{2}}=0\]
(iii) Circle with radius a and which touches both the coordinate axis.
Since, when centre more...
\[{{x}_{2}}+{{y}_{2}}-2ax-2by+{{b}_{2}}=0\]
(iii) Circle with radius a and which touches both the coordinate axis.
Since, when centre more... 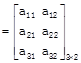
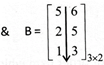 \[\therefore \,\,\,A\times B\]
\[\therefore \,\,\,A\times B\]
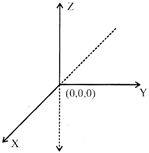 \[X'OX\xrightarrow{{}}x-axis\]
\[Y'OY\xrightarrow{{}}y-axis\]
\[Z'OZ\xrightarrow{{}}z-axis\]
Plane XOY is called xy plane
YOZ is called yz plane
and ZOX is called zx plane
In 3-D, there are 8 quadrents
Equation of x-axis be y= 0 & z =0
Equation of y-axis be x = 0 & z = 0
and equation of z-axis be x=0 & y=0
Note: In 3-D, a straight line is represented by two equations where as a plane is represented by single equation in at most three variables.
\[X'OX\xrightarrow{{}}x-axis\]
\[Y'OY\xrightarrow{{}}y-axis\]
\[Z'OZ\xrightarrow{{}}z-axis\]
Plane XOY is called xy plane
YOZ is called yz plane
and ZOX is called zx plane
In 3-D, there are 8 quadrents
Equation of x-axis be y= 0 & z =0
Equation of y-axis be x = 0 & z = 0
and equation of z-axis be x=0 & y=0
Note: In 3-D, a straight line is represented by two equations where as a plane is represented by single equation in at most three variables.
You need to login to perform this action.
You will be redirected in
3 sec
