Current Affairs 11th Class

  Structure and Physiography   Do you know that our earth also has a history. The earth and its landforms that we see today have evolved over a very long time. Current estimation shows that the earth is approximately 460 million years old. Over these long years, it has undergone many changes brought about primarily by the endogenic and exogenic forces. These forces have played a significant role in giving shape to various surface and subsurface features of the earth. You have already studied about the Plate Tectonics and the movement of the Earth's plates in the book Fundamentals of Physical Geography (NCERT, 2006). Do you know that the Indian plate was to the south of the equator millions of years ago? Do you also know that it was much larger in size and the Australian plate was a part of it? Over millions of years, this plate broke into many parts and the Australian plate moved towards the southeastern direction and the Indian plate to the north. Can you map different phases in the movement of the Indian plate? This northward movement of the Indian plate is still continuing and it has significant consequences on the physical environment of the Indian subcontinent. Can you name some important consequences of the northward movement of the Indian plate?   It is primarily through the interplay of these endogenic and exogenic forces and lateral movements of the plates that the present geological structure and geomorphologic processes active in the Indian subcontinent came into existence. Based on the variations in its geological structure and formations, India can be divided into three geological divisions. These geological regions broadly follow the physical features: (i) The Penisular Block (ii) The Himalayas and other Peninuslar Mountains (iii) Indo-Ganga-Brahmaputra Plain.   The peninsular block The northern boundary of the Peninsular Block may be taken as an irregular line running from Kachchh along the western flank of the Aravali Range near Delhi and then roughly parallel to the Yamuna and the Ganga as far as the Rajmahal Hills and the Ganga delta. Apart from these, the Karbi Anglong and the Meghalaya Plateau in the northeast and Rajasthan in the west are also extensions of this block. The northeastern parts are separated by the Malda fault in West Bengal from the Chotanagpur plateau. In Rajasthan, the desert and other desert-like features overlay this block. The Peninsula is formed essentially by a great complex of very ancient gneisses and granites, which constitutes a major part of it. Since the Cambrian period, the Peninsula has been standing like a rigid block with the exception of some of its western coast which is submerged beneath the sea and some other parts changed due to tectonic activity without affecting the original basement. As a part of the Indo-Australian Plate, it has been subjected to various vertical movements and block faulting. The rift valleys of the Narmada, the Tapi and the Mahanadi and more...

  Drainage System   You have observed water flowing through the rivers, nalas and even channels during rainy season which drain the excess water. Had these channels not been there, large-scale flooding would have occurred. Wherever channels are ill-defined or choked, flooding is a common phenomenon.   The flow of water through well-defined channels is known as 'drainage' and the network of such channels is called a 'drainage system'. The drainage pattern of an area is the outcome of the geological time period, nature and structure of rocks, topography, slope, amount of water flowing and the periodicity of the flow.   Do you have a river near your village or city?   Have you ever been there for boating or bathing?   Is it perennial (always with water) or ephemeral (water during rainy season, and dry, otherwise)? Do you know that rivers flow in the same direction? You have studied about slopes in the other two textbooks of geography (NCERT, 2006) in this class. Can you, then, explain the reason for water flowing from one direction to the other? Why do the rivers originating from the Himalayas in the northern India and the Western Ghat in the southern India flow towards the east and discharge their waters in the Bay of Bengal?         A river drains the water collected from a specific area, which is called its 'catchment area'. An area drained by a river and its tributaries is called a drainage basin. The boundary line   Important Drainage Patterns   (i) The drainage pattern resembling the branches of a tree is known as "dendritic" the examples of which are the rivers of northern plain. (ii) When the rivers originate from a hill and flow in all directions, the drainage pattern is known as 'radial'. The rivers originating from the Amarkantak range present a good example of it. (iii) When the primary tributaries of rivers flow parallel to each other and secondary tributaries join them at right angles, the pattern is known as 'trellis'. (iv) When the rivers discharge their waters from all directions in a lake or depression, the pattern is know as 'centripetal'. Find out some of the patterns in the topo sheet given in Chapter 5 of Practical Work in Geography- Part I (NCERT, 2006). 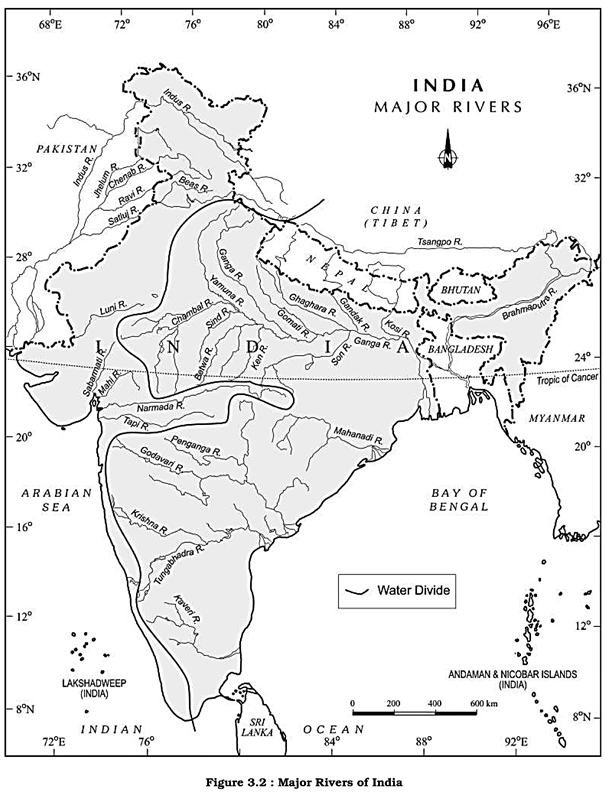        separating one drainage basin from the other is known as the watershed. The catchments of large rivers are called river basins while those of small rivulets and rills are often referred to as watersheds. There is, however, a slight difference between a river basin and a watershed. Watersheds are small in area while the basins cover larger areas.   River basins and watersheds are marked by unity. What happens in one part of the basin or watershed directly affects the other parts and the unit as a more...

  Climate   We drink more water during summers. Your uniform during the summer is different from the winters. Why do you wear lighter clothes during summers and heavy woollen clothes during winters in north India? In southern India, woollen clothes are not required. In northeastern states, winters are mild except in the hills. There are variations in weather conditions during different seasons.   These changes occur due to the changes in the elements of weather (temperature, pressure, wind direction and velocity, humidity and precipitation, etc.).   Weather is the momentary state of the atmosphere while climate refers to the average of the weather conditions over a longer period of time. Weather changes quickly, may be within a day or week but climate changes imperceptivity and may be noted after 50 years or even more.   You have already studied about the monsoon in your earlier classes. You are also aware of the meaning of the word, "monsoon".   Monsoon connotes the climate associated with seasonal reversal in the direction of winds.   India has hot monsoonal climate which is the prevalent climate in south and south East Asia.   Unity and Diversity in the Monsoon Climate  The monsoon regime emphasises the unity of India with the rest of south East Asian region. This view of broad unity of the monsoon type of climate should not, however, lead one to ignore its regional variations which differentiate the weather and climate of different regions of India. For example, the climate of Kerala and Tamil Nadu in the south are so different from that of Uttar Pradesh and Bihar in the north, and yet all of these have a monsoon type of climate. The climate of India has many regional variations expressed in the pattern of winds, temperature and rainfall, rhythm of seasons and the degree of wetness or dryness. These regional diversities may be described as sub-types of monsoon climate. Let us take a closer look at these regional variations in temperature, winds and rainfall.   While in the summer the mercury occasionally touches \[55{}^\circ C\]in the western Rajasthan, it drops down to as low as minus \[45{}^\circ C\]in winter around Leh. Churu in Rajasthan may record a temperature of \[50{}^\circ C\]or more on a June day while the mercury hardly touches \[19{}^\circ C\]in Tawang (Arunachal Pradesh) on the same day. On a December night, temperature in Drass (Jammu and Kashmir) may drop down to minus \[45{}^\circ C\]while Tiruvanantapuram or Chennai on the same night records \[20{}^\circ C\]or\[22{}^\circ C\]. These examples confirm that there are seasonal variations in temperature from place to place and from region to region in India. Not only this, if we take only a single place and record the temperature for just one day, variations are no less striking. In Kerala and in the Andaman Islands, the difference between day and night temperatures may be hardly seven or eight degree Celsius. But in the Thar more...

  Natural Vegetation   Have you ever been to a forest for a picnic? You might have surely gone to a park if you live in a city or to a mango, guava or coconut orchard, if you live in a village. How do you differentiate between the natural vegetation and the planted vegetation? The same variety may be found growing wild in the forest under natural conditions and the same tree may be the planted one in your garden under human supervision.   Natural vegetation refers to a plant community that has been left undisturbed over a long time, so as to allow its individual species to adjust themselves to climate and soil conditions as fully as possible. India is a land of great variety of natural vegetation. Himalayan heights are marked with temperate vegetation; the Western Ghats and the Andaman Nicobar Islands have tropical rain forests, the deltaic regions have tropical forests and mangroves; the desert and semi desert areas of Rajasthan are known for cactii, a wide variety of bushes and thorny vegetation. Depending upon the variations in the climate and the soil, the vegetation of India changes from one region to another.   On the basis of certain common features such as predominant vegetation type and climatic regions, Indian forests can be divided into the following groups:   Types of Forests (i) Tropical Evergreen and Semi Evergreen forests (ii) Tropical Deciduous forests (iii) Tropical Thorn forests (iv) Montane forests (v) Littoral and Swamp forests.   Tropical Evergreen and Semi Evergreen Forests These forests are found in the western slope of the Western Ghats, hills of the northeastern region and the Andaman and Nicobar Islands.   They are found in warm and humid areas with an annual precipitation of over 200 cm and mean annual temperature above\[22{}^\circ C\]. Tropical evergreen forests are well stratified, with layers closer to the ground and are covered with shrubs and creepers, with short structured trees followed by tall variety of trees. In these forests, trees reach great heights up to 60 m or above. There is no definite time for trees to shed their leaves, flowering and fruition. As such these forests appear green all the year round. Species found in these forests include rosewood, mahogony, aini, ebony, etc.   The semi evergreen forests are found in the less rainy parts of these regions. Such forests have a mixture of evergreen and moist deciduous trees. The undergrowing climbers provide an evergreen character to these forests. Main species are white cedar, hollock and kail.         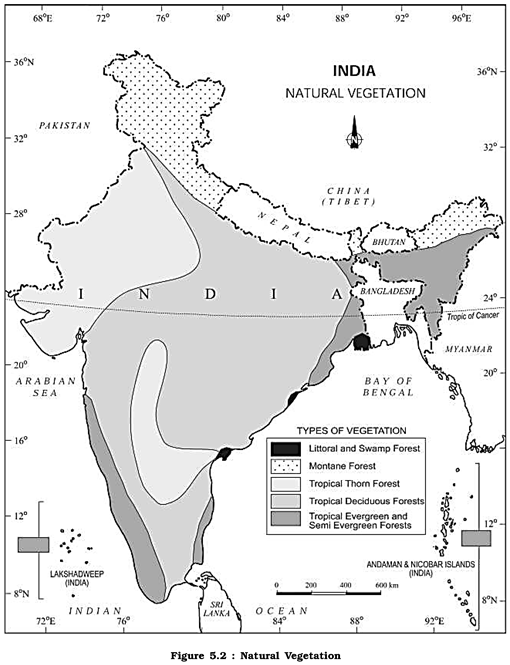The British were aware of the economic value of the forests in India, hence, large scale exploitation of these forests was started. The structure of forests was also changed. The oak forests in Garhwal and Kumaonwere replaced by pine (chirs) which was needed to lay railway more...

  Soils   Have you ever thought about the most important factor which supports trees, grasses, crops and numerous life- forms over the earth's surface? Can one grow a blade of grass without soil? While some plants and organisms which are aquatic in nature can sustain in water, do they not derive nutrients from soil through water? You will realise that soil is the most important layer of the earth's crust. It is a valuable resource. The bulk of our food and much of our clothing is derived from land-based crops that grow in the soil. The soil on which we depend so much for our day-to-day needs has evolved over thousands of years. The various agents of weathering and gradation have acted upon the parent rock material to produce a thin layer of soil.   Soil is the mixture of rock debris and organic materials which develop on the earth's surface. The major factors affecting the formation of soil are relief, parent material, climate, vegetation and other life-forms and time. Besides these, human activities also influence it to a large extent. Components of the soil are mineral particles, humus, water and air. The actual amount of each of these depend upon the type of soil. Some soils are deficient in one or more of these, while there are some others that have varied combinations.   Have you ever dug a pit in the field of your school to plant a tree while celebrating Van- Mahotsava? Was the pit of uniform layer of soil or did you notice different colours from the top to the bottom of the pit?   If we dig a pit on land and look at the soil, we find that it consists of three layers which are called horizons. 'Horizon A' is the topmost zone, where organic materials have got incorporated with the mineral matter, nutrients and water, which are necessary for the growth of plants. 'Horizon B' is a transition zone between the 'horizon A' and 'horizon C', and contains matter derived from below as well as from above. It has some organic matter in it, although the mineral matter is noticeably weathered. 'Horizon C' is composed of the loose parent material. This layer is the first stage in the soil formation process and eventually forms the above two layers. This arrangement of layers is known as the soil profile. Underneath these three horizons is the rock which is also known as the parent rock or the bedrock. Soil, which is a complex and varied entity has always drawn the attention of the scientists. In order to understand its importance, it is essential to attempt a scientific study of the soil. Classification of the soil is an effort to achieve this objective.   Classification of Soils   India has varied relief features, landforms, climatic realms and vegetation types. These have contributed in the development of various types of soils in India.   In ancient times, soils more...

  Natural Hazards and Disasters   You might have read about tsunami or seen the images of horror on television set immediately after it happened. You may also be aware of the severe earthquake in Kashmir on both sides of the Line of Control (LOC). The damage caused to human life and properties during these episodes has moved us all. What are these as phenomena and how they are caused? How can we save orselves? These are some questions which come to our minds. This chapter will attempt to analyses some of these questions.   Change is the law of nature. It is a continuous process that goes on uninterruptedly involving phenomena, big and small, material and non- material that make our physical and socio- cultural environment. It is a process present everywhere with variations in terms of magnitude, intensity and scale. Change can be a gradual or slow process like the evolution of landforms and organisms and it can be as sudden and swift as volcanic eruptions, tsunamis, earthquakes and lightening, etc. Similarly, it may remain confined to a smaller area occurring within a few seconds like hailstorms, tornadoes and dust storms, and it can also have global dimensions such as global warming and depletion of the ozone layer.   Besides these, changes have different meanings for different people. It depends upon the perspective one takes while trying to understand them. From the perspective of nature, changes are value-neutral (these are neither good nor bad). But from the human perspective, these are value-loaded. There are some changes that are desirable and good like the change of seasons, ripening of fruits, while there are others like earthquakes, floods and wars that are considered bad and undesirable.   Observe the environment you live in and prepare a list of changes, which take place over a long period of time and those, which take place within a short period of time. Do you know why some changes are considered good and others bad? Prepare a list of changes, which you notice in your daily life and give reasons why some of these are considered good and others bad.   In this chapter, we will read about some of these changes, which are considered bad and have haunted humankind for a long time.   Disasters in general and natural disasters in particular, are some such changes that are always disliked and feared by humankind.   What is a Disaster? "Disaster is an undesirable occurrence resulting from forces that are largely outside human control, strikes quickly with little or no warning, which causes or threatens serious disruption of life and property including death and injury to a large number of people, and requires therefore, mobilisation of efforts in excess of that which are normally provided by statutory emergency services".   For a long time, geographical literature viewed disasters as a consequence of natural forces; and human beings were treated as innocent and more...

  Geography as a Discipline   You have studied geography as one of the components of your social studies course upto the secondary stage. You are already aware of some of the phenomena of geographical nature in the world and its different parts. Now, you will study 'Geography' as an independent subject and leam about the physical environment of the earth, human activities and their interactive relationships. Therefore, a pertinent question you can ask at this stage is - Why should we study geography? We live on the surface of the earth. Our lives are affected by our surroundings in many ways. We depend on the resources to sustain ourselves in the surrounding areas. Primitive societies subsisted on 'natural means of subsistence', i.e. edible plants and animals. With the passage of time, we developed technologies and started producing our food using natural resources such as land, soil and water. We adjusted our food habits and clothing according to the prevailing weather conditions. There are variations in the natural resource base, technological development, adaptation with and modification of physical environment, social organisations and cultural development. As a student of geography, you should be curious to know about all the phenomena which vary over space. You learn about the diverse lands and people. You should also be interested in understanding the changes which have taken place over time. Geography equips you to appreciate diversity and investigate into the causes responsible for creating such variations over time and space. You will develop skills to understand the globe converted into maps and have a visual sense of the earth's surface. The understanding and the skills obtained in modern scientific techniques such as GIS and computer cartography equip you to meaningfully contribute to the national endeavour for development.   Now the next question which you may like to ask is - What is geography? You know that earth is our home. It is also the home of many other creatures, big and small, which live on the earth and sustain. The earth's surface is not uniform. It has variations in its physical features. There are mountains, hills, valleys, plains, plateaus, oceans, lakes, deserts and wilderness. There are variations in its social and cultural features too. There are villages, cities, roads, railways, ports, markets and many other elements created by human beings across the entire period of their cultural development.   This variation provides a clue to the understanding of the relationship between the physical environment and social/cultural features. The physical environment has provided the stage, on which human societies enacted the drama of their creative skills with the tools and techniques which they invented and evolved in the process of their cultural development. Now, you should be able to attempt the answer of the question posed earlier as to "What is geography"? In very simple words, it can be said that geography is the description of the earth. The term geography was first coined by Eratosthenese, a Greek scholar more...

  The Origin and Evolution of the Earth   Do you remember the nursery rhyme "...Twinkle, Twinkle little star..."? Starry nights have always attracted us since the childhood. You may also have thought of these stars and had numerous questions in your mind. Questions such as how many stars are there in the sky? How did they come into existence? Can one reach the end of the sky? May be many more such questions are still there in your mind. In this chapter, you will leam how these "twinkling little stars" were formed. With that you will eventually also read the story of origin and evolution of the earth.   ORIGIN OF THE EARTH   Early Theories A large number of hypotheses were put forth by different philosophers and scientists regarding the origin of the earth. One of the earlier and popular arguments was by German philosopher Immanuel Kant. Mathematician Laplace revised it in 1796. It is known as Nebular Hypothesis. The hypothesis considered that the planets were formed out of a cloud of material associated with a youthful sun, which was slowly rotating. Later in 1900, Chamberlain and Moulton considered that a wandering star approached the sun. As a result, a cigar-shaped extension of material was separated from the solar surface. As the passing star moved away, the material separated from the solar surface continued to revolve around the sun and it slowly condensed into planets. Sir James Jeans and later Sir Harold Jeffrey supported this argument. At a later date, the arguments considered of a companion to the sun to have been coexisting. These arguments are called binary theories. In 1950, Otto Schmidt in Russia and Carl Weizascar in Germany somewhat revised the 'nebular hypothesis', though differing in details. They considered that the sun was surrounded by solar nebula containing mostly the hydrogen and helium along with what may be termed as dust. The friction and collision of particles led to formation of a disk-shaped cloud and the planets were formed through the process of accretion.   Modern Theories However, scientists in later period took up the problems of origin of universe rather than that of just the earth or the planets. The most popular argument regarding the origin of the universe is the Big Bang Theory. It is also called expanding universe hypothesis. Edwin Hubble, in 1920, provided evidence that the universe is expanding. As time passes, galaxies move further and further apart. You can experiment and find what the expanding universe means. Take a balloon and mark some points on it to represent the galaxies. Now, if you start inflating the balloon, the points marked on the balloon will appear to be moving away from each other as the balloon expands. Similarly, the distance between the galaxies is also found to be increasing and thereby, the universe is considered to be expanding. However, you will find that besides the increase in the distances between more...

  Interior of the Earth   What do you imagine about the nature the earth? Do you imagine it to be solid ball like cricket ball or a hollow ball with a thick cover of rocks i.e. lithosphere? Have you ever seen photographs or images of a volcanic eruption on the television screen? Can you recollect the emergence of hot molten lava, dust, smoke, fire and magma flowing out of the volcanic crater?   The interior of the earth can be understood only by indirect evidences as neither any one has nor anyone can reach the interior of the earth.   The configuration of the surface of the earth is largely a product of the processes operating in the interior of the earth. Exogamic as well as endogenic processes are constantly shaping the landscape. A proper understanding of the physiographic character of a region remains incomplete if the effects of endogenic processes are ignored. Human life is largely influenced by the physiography of the region. Therefore, it is necessary that one gets acquainted with the forces that influence landscape development. To understand why the earth shakes or how a tsunami wave is generated, it is necessary that we know certain details of the interior of the earth. In the previous chapter, you have noted that the earth-forming materials have been distributed in the form of layers from the crust to the core. It is interesting to know how scientists have gathered information about these layers and what the characteristics of each of these layers are. This is exactly what this chapter deals with.   Sources of information about the interior   The earth's radius is 6,370 km. No one can reach the centre of the earth and make observations or collect samples of the material. Under such conditions, you may wonder how scientists tell us about the earth's interior and the type of materials that exist at such depths. Most of our knowledge about the interior of the earth is largely based on estimates and inferences. Yet, a part of the information is obtained through direct observations and analysis of materials. Direct Sources The most easily available solid earth material is surface rock or the rocks we get from mining areas. Gold mines in South Africa are as deep as 3 - 4 km. Going beyond this depth is not possible as it is very hot at this depth. Besides mining, scientists have taken up a number of projects to penetrate deeper depths to explore the conditions in the crustal portions. Scientists world over are working on two major projects such as "Deep Ocean Drilling Project" and "Integrated Ocean Drilling Project". The deepest drill at Kola, in Arctic Ocean, has so far reached a depth of 12 km. This and many deep drilling projects have provided large volume of information through the analysis of materials collected at different depths.   Volcanic eruption forms another source of obtaining direct more...

  Distribution of Oceans and Continents   In the previous chapter, you have studied the interior of the earth. You are already familiar with the world map. You know that continents cover 29 per cent of the surface of the earth and the remainder is under oceanic waters. The positions of the continents and the ocean bodies, as we see them in the map, have not been the same in the past. Moreover, it is now a well-accepted fact that oceans and continents will not continue to enjoy their present positions in times to come. If this is so, the question arises what were their positions in the past? Why and how do they change their positions? Even if it is true that the continents and oceans have changed and are changing their positions, you may wonder as to how scientists know this. How have they determined their earlier positions? You will find the answers to some of these and related questions in this chapter.   Continental Drift Observe the shape of the coastline of the Atlantic Ocean. You will be surprised by the symmetry of the coastlines on either side of the ocean. No wonder, many scientists thought of this similarity and considered the possibility of the two Americas, Europe and Africa, to be once joined together. From the known records of the history of science, it was Abraham Ortelius, a Dutch map maker, who first proposed such a possibility as early as 1596. Antonio Pellegrini drew a map showing the three continents together. However, it was Alfred Wegener - a German meteorologist who put forth a comprehensive argument in the form of "the continental drift theory" in 1912. This was regarding the distribution of the oceans and the continents.   According to Wegener, all the continents formed a single continental mass, a mega ocean surrounded by the same. The super continent was named PANGAEA, which meant all earth. The mega-ocean was called PANTHALASSA, meaning all water. He argued that, around 200 million years ago, the super continent, Pangaea, began to split. Pangaea first broke into two large continental masses as Laurasia and Gondwanaland forming the northern and southern components respectively. Subse - quently, Laurasia and Gondwanaland continued to break into various smaller continents that exist today. A variety of evidence was offered in support of the continental drift. Some of these are given below.   Evidence in Support of the Continental Drift   The Matching of Continents (Jig-Saw-Fit) The shorelines of Africa and South America facing each other have a remarkable and unmistakable match. It may be noted that a map produced using a computer programme to find the best fit of the Atlantic margin was presented by Bullard in 1964. It proved to be quite perfect. The match was tried at 1,000 fathom line instead of the present shoreline.   Rocks of Same Age across the Oceans The radiometric dating methods developed in the recent period have more...