Current Affairs 11th Class

Category : 11th Class

 

Two Dimensional Geometry (Coordinate and Straight Line)

 

Key Points to Remember

 

• Coordinate Geometry: It is the branch of mathematics in which deal with relation between two variable in algebraic form. It is 1st coined by French Mathematician Rene Descarties.

 

Let P(x, y) be any point

 

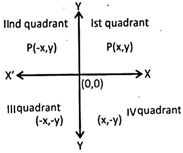
x\[\to \] abscissa

y\[\to \] ordinate

 

• Some Basic Formula:
• Distance Formula:

 

(a)        The distance between two points \[A({{x}_{1}},\,{{y}_{1}})\] & \[B({{x}_{2}},\,{{y}_{2}})\]

 

\[Ab=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]

 

 

       

(b)        Distance between the origin 0(0, 0) and the point P(x, y) is OP

                       

\[op=\sqrt{{{x}^{2}}+{{y}^{2}}}\]

 

e.g.\[A=(5,3)\,\,\,B=(-2,5)\]

\[\therefore \,\,\,AB\]

           

\[=\sqrt{{{(-2-5)}^{2}}{{(5-3)}^{2}}}=\sqrt{49+4}=\sqrt{53}\]

 

• Section Formula: The coordinate of the point P(x, y) dividing the line segment joining the two points \[A({{x}_{1}},{{y}_{1}})\] and \[B({{x}_{2}},y{{  }_{2}})\] internally in the ratio m:n are given by

\[x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\] \[y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n},\]

 

 

 

 

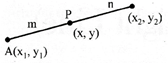
When P divides AB in the ratio m:n then

 

\[x=\frac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\] \[y=\frac{m{{y}_{2}}-n{{y}_{1}}}{m-n},\]

           

When P divides AB in the ratio 1:1 i.e. P is the mid point of AB

 

\[\therefore \,\,\,\text{P}\equiv \text{(x,y)=}\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{2}}+{{y}_{1}}}{2} \right)\]

 

• Area of triangle: A, B & C be the vertices of the triangle ABC such that \[A\equiv ({{x}_{1}},{{y}_{1}}),\] \[B\equiv ({{x}_{2}},{{y}_{2}}),\] & \[C\equiv ({{x}_{3}},{{y}_{3}}),\]

Area of ABC

                       

\[=\frac{1}{2}\{{{x}_{1}}({{y}_{2}}-{{y}_{3}})+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}})\}\]

 

       

 

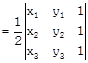
[Using determinant form]

 

• Area of a quadrilateral: The ara of the quadraleteral, whose vertices are \[A({{x}_{1}},{{y}_{1}}),\] \[B({{x}_{2}},{{y}_{2}}),\] \[C({{x}_{3}},{{y}_{3}}),\]& \[D({{x}_{4}},{{y}_{4}}),\] is

 

 

Note: The rule for writting the area of a quadrilateral is the same as that of a triangle.

Similarly, we can find the area of a polygon of n sides with vertices \[{{A}_{1}}({{x}_{1}},{{y}_{1}}),{{A}_{2}}({{x}_{2}},{{y}_{2}})...{{A}_{n}}({{x}_{n}},{{y}_{n}})\]is

 

 

If \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\,\,{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\] and \[{{a}_{3}}x+{{b}_{3}}y+{{c}_{3}}=0\] are the equation of the triangle. Then the area of the triangle be

 

 

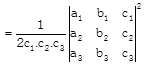
Where \[{{c}_{1}},\,{{c}_{2}},\,{{c}_{3}}\] be the co-factor of \[{{c}_{1}},\,{{c}_{2}},\,{{c}_{3}}\] in the determinants:

\[\therefore \,\,\,{{c}_{1}}={{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{2}},\]

\[{{c}_{2}}={{a}_{3}}.{{b}_{1}}-{{a}_{1}}{{b}_{3}}\]

& \[{{c}_{3}}={{a}_{1}}.{{b}_{2}}-{{a}_{2}}{{b}_{1}}.\]

 

• Condition of collinearity of three points: The three point \[A({{x}_{1}},{{y}_{1}}),\] \[B({{x}_{2}},{{y}_{2}})\] and \[C({{x}_{3}},{{y}_{3}})\] are collinear iff \[\Delta ABC=0\]

 

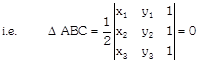
[In determinant form]

 

Solved Problem

 

1. Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear.

Sol.      Let \[A\equiv (a,b+c)\]

\[B\equiv (b,c+a)\]

\[C\equiv (c,a+b),\] be three point.

To show the collinear of the points A, B and C.

Area of \[\Delta ABC\] should be zero.

Now,

 

 

 

 

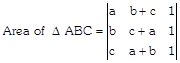
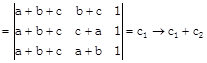
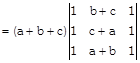
[Two columns are identical]

 

\[=(a+b+c)\times 0=0\]

 

Hence the points. A, B & C be collinear.

 

Straight Lines

 

• Definiton: It is the locus of the points which moves such that every point on the line segment joining any two points lies on it.
• General Equation of a straight line: An equation of the form \[ax+by+c=0.\] Where a, b, c are any real numbers not all zero, always represents a straight line. Equation of the straight line is always of first degree in x & y.
• Slope of line: If a tine makes on angle \[\theta \left( \theta \ne \frac{\pi }{2} \right)\] with the position direction of the x-axis. Slope or gradiant of that line is usually denoted by \[m=\tan \theta \]
• The slope of a line parallel to x-axis = 0
• If the three points A, B, C be callinear, then slope of AB= slope of BC= slope of CA.
• If \[A\equiv ({{x}_{1}},{{y}_{2}})\] & \[B\equiv ({{x}_{2}},{{y}_{2}})\] be two point then slope of \[AB=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]

 

• Angle between two lines: The angle q between the lines having slope \[{{m}_{1}}\] and \[{{m}_{2}}\] is written as tan

 

\[\theta =\frac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}\]

 

Note:    If the lines are parallel then

\[\tan \theta =0\]

 

i.e.        \[\frac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}=0\]

 

\[\Rightarrow {{m}_{1}}={{m}_{2}}\]

i.e. if two lines are parallel then their slopes are equal.

 

• Condition of perpendicularity of two line: If two lines of slopes \[{{m}_{1}}\] and \[{{m}_{2}}\] are perpendicular then the angle \[\theta \] between then is of \[90{}^\circ \]

\[\tan \theta =\infty \] i.e.

 

\[\frac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}=\infty =\frac{1}{0}\]

 

\[\Rightarrow 1+{{m}_{1}}.{{m}_{2}}=0\]

 

\[\Rightarrow {{m}_{1}}.{{m}_{2}}=-1\]

i.e.        The product of their slopes is equal to -1.

 

1. If the angle between two lines is \[\frac{\mathbf{\pi }}{\mathbf{4}}\] and the slope of one of the line is \[\frac{\mathbf{1}}{\mathbf{2}}\] then find the slope of the other lines.

 

Sol.      Given \[\theta \frac{\pi }{4}\]

                       

& \[{{m}_{1}}=\frac{1}{2}\]

\[\because \]       Angle between two lines in tangent form is written as

           

            \[\tan \theta =\left| \frac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}.{{m}_{2}}} \right|\] (when q is in acute angle) \[\tan \frac{\pi }{4}=\left| \frac{\frac{1}{2}-{{m}_{2}}}{1+\frac{1}{2}{{m}_{2}}} \right|\]

                       

            \[\Rightarrow \pm 1=\frac{\frac{1}{2}-{{m}_{2}}}{1+\frac{1}{2}{{m}_{2}}}\]

 

            \[1+\frac{1}{2}{{m}_{2}}=\frac{1}{2}-{{m}_{2}}\] (Taking positive sign)

                       

            \[\Rightarrow \frac{1}{2}{{m}_{2}}+{{m}_{2}}=\frac{1}{2}-1=-\frac{1}{2}\]

 

            \[\frac{3}{2}{{m}_{2}}=\frac{-1}{2}\]

 

            \[\therefore \,\,\,\,\,{{m}_{2}}=\frac{-1}{3}\]

                       

Again taking negative sign

 

\[\therefore \,\,\,\,\frac{\frac{1}{2}-{{m}_{2}}}{1+\frac{1}{2}{{m}_{2}}}=-1\Rightarrow {{m}_{2}}=3\]

 

Hence the slope of the other line is \[\frac{-1}{3}\] or 3.

 

Intercept of a line on the axes: Intercept of a line on axis: If a straight line cuts x-axis at A and the y-axis at B then OA & OB is said to be the intercept of the line of x-axis & y-axis respectively.

 

 

·                   

• Equation of lines parallel to axis

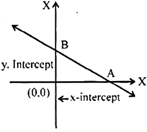
(i)         Equation of x-axis is \[y=0\]

(ii)        Equation of y-axis is \[x=0\]

(iii)       Equation of a line parallel to x-axis be \[y=b\]

(iv)       If the line is parallel to x-axis, at the distance, b from it and is an negative side of y axis, then its equation is \[y=-b\]

(v)        Equation of a Ine parallel to y-axis is \[x=+a\]

(vi)       If the line is parallel to y-axis, at distance a from it and is on the negative side of x-axis, then its equation is \[x=-a\]

 

Equation of a straight line in various forms

 

                      Slope-Intercept form

 

 

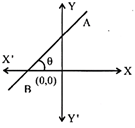
The equation of a straight line whose slope is m and which cuts an intercept c on the y-axis is given by \[y=mx+c\]

If the line passes through the origin, then \[c=0\] and hence the equation of the line be \[y=mx\]

 

Solved Problem

 

1. Find the equation of the straight one which intersect y-axis at distance of 2 units above the origin and making an angle of \[\mathbf{30{}^\circ }\] with the positive direction of x-axis.

 

Sol.      Here \[c=2\] unit

\[\theta =30{}^\circ \]

 

so, \[m=\tan \theta =\tan 30{}^\circ =\frac{1}{\sqrt{3}}\]

Hence the required equation of straight line be

\[y=mx+c\]

 

\[y=\frac{1}{\sqrt{3}}x\times 2\]

 

\[\Rightarrow \,\,\,x-\sqrt{3}y+2\sqrt{3}=0\]

 

• Point-slope form: The equation of the straight line passing through the point (x, y) and having slope m is written as \[y-{{y}_{1}}=m(x-{{x}_{1}})\]

 

Solved Problem

 

1. Find the equation of the straight line which is passing through \[(2,\,2\sqrt{3})\] and inclined with the x-axis at an angle of \[75{}^\circ \]

 

Sol.      Here, given be

\[P\equiv (2,2\sqrt{3}),\theta \equiv 75{}^\circ \]

Slope of straight line, \[m=\tan \theta =\tan 75{}^\circ \]

 

\[\tan (45{}^\circ +30{}^\circ )=\frac{\tan 45{}^\circ +\tan 30{}^\circ }{1-\tan 45{}^\circ .\tan 30{}^\circ }=\frac{1+\frac{1}{\sqrt{3}}}{1-\frac{1}{\sqrt{3}}\times 1}=\frac{\sqrt{3}+1}{\sqrt{3}-1}=\frac{\sqrt{3}+1}{\sqrt{3}-1}\times \frac{\sqrt{3}+1}{\sqrt{3}-1}\]

 

\[=\frac{\sqrt{3}+1{{)}^{2}}}{(\sqrt{3{{)}^{2}}-{{(1)}^{2}}}}=\frac{{{(\sqrt{3}+1)}^{2}}+{{1}^{2}}+2\sqrt{3}.1}{3-1}=\frac{4+2\sqrt{3}}{2}=2+\sqrt{3}\]

 

Hence, the required equation of straight line be

\[y-{{y}_{1}}=m(x-{{x}_{1}})\]

\[y-2\sqrt{3}=(2+\sqrt{3})(x-2)\]

\[\Rightarrow \,\,\,(2+\sqrt{3})x-y+4-2\sqrt{3}\]

\[\Rightarrow \,\,\,(2+\sqrt{3})x-y+4-0\]

 

• Two-point form: The equation of a straight line passing through two points \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is written as \[(y-{{y}_{1}})=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}(x-{{x}_{1}})\]

 

Solved Problem

 

1. Find the equation of straight line which is passing through the points \[\mathbf{A(-1,}\,\mathbf{1)}\] & \[\mathbf{B(2,}\,\mathbf{-4)}\mathbf{.}\]

 

Sol:      Slope of AB line \[=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{-4-1}{2-(-1)}=\frac{-5}{3}\]

 

Thus, the equation of straight line AB be

                        \[y-{{y}_{1}}=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}(x-{{x}_{1}})\]

                       

                        \[\Rightarrow \,\,y-1=\frac{-5}{3}(x+1)\]

                       

\[\Rightarrow \,\,5x+3y-3+5=0\]

\[\Rightarrow \,\,5x+3y+2=0\]

 

Intercept form

 

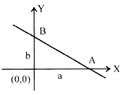
The equation of a straight line which cuts off intercepts a & b. an x-axis & y-axis respectively is written as \[\frac{x}{a}+\frac{y}{b}=1\]

 

1. Find the equation of the line that cuts off equal intercepts on the coordinate axes and passing through the point (2, 3)

 

Sol.      The equation of straight line in intercept form be

                       

            \[\frac{x}{a}+\frac{y}{b}=1\]

since, line cuts off equal intercept on the coordinate axes.

i.e. \[a=b\]

 

then equation of straight line be \[\frac{x}{a}+\frac{y}{b}=1\]

 

            \[\Rightarrow \,\,\,x+y=a\]

According to the question

straight line passes through (2, 3)

then \[2+3=a\Rightarrow a-5\]

Thus, the required equation of the straight line be

x+y=5=>x+y-5=0

 

Normal Form (or perpendicular Form):

 

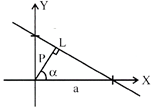
The equation of a straight line having the length of the perpendicular from the origin is p and the perpendicular makes an angle a with the positive direction of x-axis is written as \[x.\cos \theta =y.\sin \theta =p\]

 

Note:    In normal form of equation of a straight line is always taken as the positive and \[\theta \] is measured from the positive direction of x-axis in anticlockwise direction between 0 and \[2\pi \]

 

15. Find the equation of the line whose perpendicular distance from the origin is 4 units & the angle which the normal makes with the positive direction of x-axis is 15.

 

Sol.      Here \[p=4\]unit

                        \[\theta =15\]

            Equation of the straight line be

            \[x.\cos \theta +y\sin \theta =p\]

            \[x.\cos 15{}^\circ +y.\sin 15{}^\circ =4\]

            \[\because \] Now, \[\cos 15{}^\circ =\cos (45{}^\circ -30{}^\circ )\]

            \[\cos 45{}^\circ .\cos 30{}^\circ +\sin 45{}^\circ .\sin 30{}^\circ \]

           

            \[=\frac{1}{\sqrt{2}}.\frac{\sqrt{3}}{2}+\frac{1}{\sqrt{2}}.\frac{1}{2}=\frac{\sqrt{3}-1}{2\sqrt{2}}\]

 

Similarly, \[\sin 15{}^\circ =\frac{\sqrt{3}-1}{2\sqrt{2}}\]

 

Thus, the required equation of the straight line in normal form be

                        \[x.\frac{\sqrt{3}+1}{2\sqrt{2}}+y.\frac{\sqrt{3}-1}{2\sqrt{2}}=4\]

                       

                        \[(\sqrt{3}+1)x+(\sqrt{3}-1)y=8\sqrt{2}\]

 

Parametric Form (or Symmetric form)

 

 

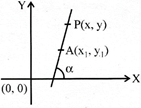
The equation of a straight line passing through the point \[({{x}_{1}},\,{{y}_{1}})\] & making an angle a with the positive direction of x-axis is written as \[\frac{x-{{x}_{1}}}{\cos \alpha }=\frac{y-{{y}_{1}}}{\sin \alpha }=r\]

 

Where r is the distance of the point (x, y) from the point \[({{x}_{1}},\,{{y}_{1}}).\]

 

 

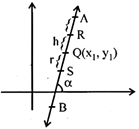
Note: If \[Q({{x}_{1}},\,{{y}_{1}})\] be a point on a line AB which makes an angle a with the positive direction of the x-axis, then there will be two points on line AB at distance r from \[Q({{x}_{1}},\,{{y}_{1}})\]  and their coordinate will be

\[({{x}_{1}}+r\,\,\cos \theta ,{{y}_{1}}+r\sin \theta )\] and \[({{x}_{1}}-r\,\,\cos \theta ,{{y}_{1}}-r\sin \theta )\]

Reduction (Derived) of the General Equation to the different standard form.

 

Slope-Intercept form

The general equation of straight line,

\[Ax+By+c=0,\] can be reduced to the form \[y=mx+c\] by expressing y as:

           

                        \[y=\frac{-Ax-C}{B}=\left( \frac{-A}{B} \right)x+\left( \frac{-C}{B} \right)\]

                        i.e.        \[m=\frac{-A}{B}\] & \[{{c}_{1}}=\frac{-C}{B}\]

i.e. the slope of the straight line

                        \[Ax+By+C=0\] be

           

\[m=\frac{-A}{B}=\frac{-coe\text{ff}icient\,of\,x}{coe\text{ff}icient\,of\,y}\]

           

&          \[y-\operatorname{intercept},{{c}_{1}}=\frac{C}{B}=\frac{-cons\operatorname{tant}\,term}{coe\text{ff}icient\,of\,y}\]

 

• Intercept form

 

If \[C\ne 0\]

\[\because \]       equation of straight line be

\[Ax+By+C=0\]

\[Ax+By=-C\]

 

Dividing both sides by -C, we have

           

\[\frac{Ax}{-C}+\frac{By}{-C}=1\]

           

\[\Rightarrow \frac{x}{\left( \frac{-C}{A} \right)}+\frac{y}{\left( \frac{-C}{B} \right)}=1\]

which is of the form \[\frac{x}{a}+\frac{y}{b}=1\]

 

\[\therefore \,\,a=\frac{-C}{A}\] & \[b=\frac{-C}{B}\]

 

lf \[C=0\]

Then the general equation of the straight line \[ax+By+c=0,\] be

i.e. \[Ax+By=0\,\,(\because c=0)\] will be passing through the origin.

 

• Normal form: To reduce the equation \[Ax+By+C=0\,\,\] to the form \[x.\cos \theta +y.\sin \theta =p.\]

1st express it as:

\[Ax+By=-C\]               ...... (i)

Case- I: If \[C<0\] or \[-C>0.\]

 

Dividing both sides of equation (i) by \[\sqrt{{{A}^{2}}+{{B}^{2}}},\] we have \[\frac{Ax}{\sqrt{{{A}^{2}}+{{B}^{2}}}}+\frac{By}{\sqrt{{{A}^{2}}+{{B}^{2}}}}=\frac{-C}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\]

 

which is of the form \[x.\cos \theta +y.\sin \theta =p\]

 

where \[\cos \theta =\frac{A}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\]

 

            \[\sin \theta =\frac{B}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\] & \[p=\frac{-C}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\]

 

Case- II: If \[C>0\]or \[-C<0\]

 

Then dividing the equation (i) by \[-\sqrt{{{A}^{2}}+{{B}^{2}}},\] we have \[\frac{-Ax}{\sqrt{{{A}^{2}}+{{B}^{2}}}}-\frac{By}{\sqrt{{{A}^{2}}+{{B}^{2}}}}.y=\frac{C}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\]

Which is of the form \[x\cos \theta +y\sin \theta =p\]

 

Carollary: The length of the perpendicular from the origin on the straight line

           

\[Ax+By+C=0\] is \[\frac{\left| C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\]

Tips: 1^st of all,

 

(i)         Transpose the constant terms in the R.H.S.

(ii)        Then make the constant term positive if it is not already so (this may be done by multiplying throughout by -1 if necessary).

(iii)       Divide both sides by

           

\[\sqrt{{{(coe\text{ff}icient\,\,of\,\,x)}^{2}}+{{(coe\text{ff}icient\,\,of\,\,y)}^{2}}}\]

 

(iv)       Now coefficient of \[x=\cos \theta \]

coefficient of \[y=\sin \theta \]

& R.H.S = p

Condition for two straight line to be coincident, parallel, perpendicular or intersecting.

Two lines \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\]

 

1. coincident, if \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\]

 

2. Parallel, if \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\]

 

3. Perpendicular, if \[{{a}_{1}}.{{a}_{2}}+{{b}_{2}}.{{b}_{2}}=0\]

 

4. Intersecting, if \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\]

 

i.e. They are neither coincident nor parallel.