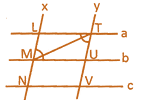
 Proof:
Since \[\text{LT }\!\!|\!\!\text{ }\,\text{ }\!\!|\!\!\text{ MU}\] and \[~\text{LM }\!\!|\!\!\text{ }\,\text{ }\!\!|\!\!\text{ TU}\]
\[\therefore \] LMUT is a parallelogram \[\therefore \] TU = LM .....(i)
Similarly
MNVU is a parallelogram
\[\therefore \] MN=UV .....(ii)
But \[\therefore \] TU = UV
Now In
\[\Delta \text{MLT}\]and \[\Delta \text{TUM}\] (Alternate)
\[\angle \text{MTL}=\angle \text{MTU}\] (Opposite angle of Parallelogram)
LT = UM (Opposite sides of Parallelogram)
MT=MT (Common)
\[\therefore \] By SOS
\[\Delta \text{MTL}\cong \Delta \text{TUM}\]
By CPCT,
LM=TU
Similarly
MN=UV But
LM=MN
\[\therefore \] TU = UV
Proof:
Since \[\text{LT }\!\!|\!\!\text{ }\,\text{ }\!\!|\!\!\text{ MU}\] and \[~\text{LM }\!\!|\!\!\text{ }\,\text{ }\!\!|\!\!\text{ TU}\]
\[\therefore \] LMUT is a parallelogram \[\therefore \] TU = LM .....(i)
Similarly
MNVU is a parallelogram
\[\therefore \] MN=UV .....(ii)
But \[\therefore \] TU = UV
Now In
\[\Delta \text{MLT}\]and \[\Delta \text{TUM}\] (Alternate)
\[\angle \text{MTL}=\angle \text{MTU}\] (Opposite angle of Parallelogram)
LT = UM (Opposite sides of Parallelogram)
MT=MT (Common)
\[\therefore \] By SOS
\[\Delta \text{MTL}\cong \Delta \text{TUM}\]
By CPCT,
LM=TU
Similarly
MN=UV But
LM=MN
\[\therefore \] TU = UV 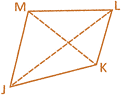 (i) Points J, K, L and M are the vertices of quadrilateral JKLM.
(ii) The line segments J, K, L, LM and JM are the sides of this quadrilateral.
(iii) The two sides of a quadrilateral having a common point is called adjacent side.
(iv) The two sides have no common end point is called opposite side.
(v) Two angles of a quadrilateral having common arm is called adjacent angle.
(vi) Two angles of a quadrilateral having no common arm is called vertically opposite angles.
(i) Points J, K, L and M are the vertices of quadrilateral JKLM.
(ii) The line segments J, K, L, LM and JM are the sides of this quadrilateral.
(iii) The two sides of a quadrilateral having a common point is called adjacent side.
(iv) The two sides have no common end point is called opposite side.
(v) Two angles of a quadrilateral having common arm is called adjacent angle.
(vi) Two angles of a quadrilateral having no common arm is called vertically opposite angles.
 Proof:
In \[\Delta \text{PQR}\]
\[\angle \text{Q}+\angle \text{QPR}+\angle \text{QRP}=\text{18}0{}^\circ \] .....(i)
In \[\Delta \text{PRS}\] \[\angle \text{S}+\angle \text{SRP}+\angle \text{SPR}=\text{18}0{}^\circ \] .....(ii)
Adding (i) and (ii), we get:
\[\angle \text{Q}+\angle \text{S}+(\angle \text{QPR}+\angle \text{SPR})+(\angle \text{QRP}+\angle \text{SRP})=\text{36}0{}^\circ \]
\[\Rightarrow \] \[\angle \text{Q}+\angle \text{S}+\angle \text{P}+\angle \text{R}=\text{36}0{}^\circ \]
[Because \[\angle \text{QPR}+\angle \text{SPR}=\angle \text{P},\angle \text{QRP}+\angle \text{SRP}=\angle \text{R}\]]
Hence, proved
Theorem 2:
In a parallelogram opposite sides and opposite angles are equal and diagonals bisect each other.
Given:
A parallelogram PQSR, PQ II RS and PS II QR
To Prove:
(i) \[\text{PQ}=\text{RS},~~~~\text{PS}=\text{QR}\]
(ii) \[\angle \text{P}=\angle \text{R}\] and \[\angle \text{Q}=\angle \text{S}\]
(iii) 0 is the midpoint of PR and SQ
Proof:
In \[\Delta \text{PQR}\]
\[\angle \text{Q}+\angle \text{QPR}+\angle \text{QRP}=\text{18}0{}^\circ \] .....(i)
In \[\Delta \text{PRS}\] \[\angle \text{S}+\angle \text{SRP}+\angle \text{SPR}=\text{18}0{}^\circ \] .....(ii)
Adding (i) and (ii), we get:
\[\angle \text{Q}+\angle \text{S}+(\angle \text{QPR}+\angle \text{SPR})+(\angle \text{QRP}+\angle \text{SRP})=\text{36}0{}^\circ \]
\[\Rightarrow \] \[\angle \text{Q}+\angle \text{S}+\angle \text{P}+\angle \text{R}=\text{36}0{}^\circ \]
[Because \[\angle \text{QPR}+\angle \text{SPR}=\angle \text{P},\angle \text{QRP}+\angle \text{SRP}=\angle \text{R}\]]
Hence, proved
Theorem 2:
In a parallelogram opposite sides and opposite angles are equal and diagonals bisect each other.
Given:
A parallelogram PQSR, PQ II RS and PS II QR
To Prove:
(i) \[\text{PQ}=\text{RS},~~~~\text{PS}=\text{QR}\]
(ii) \[\angle \text{P}=\angle \text{R}\] and \[\angle \text{Q}=\angle \text{S}\]
(iii) 0 is the midpoint of PR and SQ
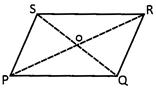 Proof:
In\[\Delta \text{PQR}\]and\[\Delta \text{RSP}\]
\[\angle \text{RPQ}=\angle \text{PRS},\] (Alternate)
\[\angle \text{PRQ}=\angle \text{RPS}\]
and \[PR=PR\] (Common)
\[\Delta \text{PQR}=\Delta \text{PRS}\]
By C.P.C.T. (Corresponding part of congruence triangle PQ = RS, and PS = QR and\[\angle \text{Q}=\angle \text{S}\].
Similarly In
\[\Delta \text{PQS}\] and \[\Delta \text{QSR}\]
we get:
\[\Delta P\text{QS}\cong \Delta QSS\]
\[\Rightarrow \] \[\angle P=\angle R\]
so,
\[PQ=RS\] and \[PS=QR\] Proved
\[\angle P=\angle R\] and \[\angle Q=\angle S\] Proved
Now In
\[\Delta \text{POQ}\] and \[\Delta \text{ROS}\]
\[\angle \text{OPQ}=\angle \text{ORS}\] (Alternate)
\[\angle \text{OQP}=\angle \text{OSR}\]
And \[\text{PQ}=\text{QR}\] (Opposite of Parallelogram)
\[\Rightarrow \] \[\Delta POQ\cong \Delta SOR\] (By ASA)
\[\Rightarrow \] PO = OR and QO = OS (By CPCT)
\[\Rightarrow \] O is the midpoint of PR and QS (Hence, proved)
Proof:
In\[\Delta \text{PQR}\]and\[\Delta \text{RSP}\]
\[\angle \text{RPQ}=\angle \text{PRS},\] (Alternate)
\[\angle \text{PRQ}=\angle \text{RPS}\]
and \[PR=PR\] (Common)
\[\Delta \text{PQR}=\Delta \text{PRS}\]
By C.P.C.T. (Corresponding part of congruence triangle PQ = RS, and PS = QR and\[\angle \text{Q}=\angle \text{S}\].
Similarly In
\[\Delta \text{PQS}\] and \[\Delta \text{QSR}\]
we get:
\[\Delta P\text{QS}\cong \Delta QSS\]
\[\Rightarrow \] \[\angle P=\angle R\]
so,
\[PQ=RS\] and \[PS=QR\] Proved
\[\angle P=\angle R\] and \[\angle Q=\angle S\] Proved
Now In
\[\Delta \text{POQ}\] and \[\Delta \text{ROS}\]
\[\angle \text{OPQ}=\angle \text{ORS}\] (Alternate)
\[\angle \text{OQP}=\angle \text{OSR}\]
And \[\text{PQ}=\text{QR}\] (Opposite of Parallelogram)
\[\Rightarrow \] \[\Delta POQ\cong \Delta SOR\] (By ASA)
\[\Rightarrow \] PO = OR and QO = OS (By CPCT)
\[\Rightarrow \] O is the midpoint of PR and QS (Hence, proved)  (iv) The distance between line and points lying on it is always zero.
(v) The sum of any two sides of a triangle is greater than the third side.
(vi) The difference between any two sides of a triangle is always less than its third side.
(iv) The distance between line and points lying on it is always zero.
(v) The sum of any two sides of a triangle is greater than the third side.
(vi) The difference between any two sides of a triangle is always less than its third side.


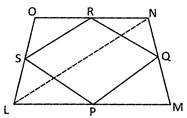 To Prove:
PQRS is a parallelogram
Construction:
Join LN
Proof:
In\[\Delta \text{LMN}\],
\[PQ\,|\,\,|\,LN\] and \[\text{PQ}=\frac{1}{2}\text{LN}\] ...,.(i)
[Because P and Q are the mid points of LM and MN respectively]
In \[\Delta \text{LNO}\]
\[SR\,|\,\,|LN\] and \[\text{SR}=\frac{1}{2}\text{LN}\] .....(ii)
[Because S and R are the mid - points of LO and ON respectively]
From (i) and (ii), we get
\[\text{PQ}=\text{SR}\] and \[~\text{PQ}\,\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }\,\text{SR}\] ....(iii)
Similarly we can see that
\[\text{PS}=\text{QR}\] and \[\text{PS}\,\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }\,\text{QR}\] .....(iv)
From (iii) and (iv), we conclude that quadrilateral PQRS more...
To Prove:
PQRS is a parallelogram
Construction:
Join LN
Proof:
In\[\Delta \text{LMN}\],
\[PQ\,|\,\,|\,LN\] and \[\text{PQ}=\frac{1}{2}\text{LN}\] ...,.(i)
[Because P and Q are the mid points of LM and MN respectively]
In \[\Delta \text{LNO}\]
\[SR\,|\,\,|LN\] and \[\text{SR}=\frac{1}{2}\text{LN}\] .....(ii)
[Because S and R are the mid - points of LO and ON respectively]
From (i) and (ii), we get
\[\text{PQ}=\text{SR}\] and \[~\text{PQ}\,\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }\,\text{SR}\] ....(iii)
Similarly we can see that
\[\text{PS}=\text{QR}\] and \[\text{PS}\,\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }\,\text{QR}\] .....(iv)
From (iii) and (iv), we conclude that quadrilateral PQRS more... 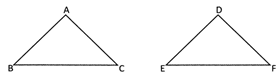 (ii) Two triangles ABC and DEF are said to be congruent if:
(a) AB = DE, BC = EF and CA = FD
(b) \[\angle \text{A}=\angle \text{D,}\,\angle \text{B}=\angle \text{E}\] and\[\angle \text{C}=\angle \text{F}\]
(ii) Two triangles ABC and DEF are said to be congruent if:
(a) AB = DE, BC = EF and CA = FD
(b) \[\angle \text{A}=\angle \text{D,}\,\angle \text{B}=\angle \text{E}\] and\[\angle \text{C}=\angle \text{F}\]
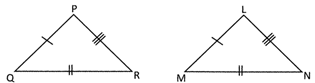 In the above given figure \[\Delta PQR\] and \[\Delta LMN\] in such a way that
\[\text{PQ}=\text{LM},\text{ QR}=\text{MN},\text{ PR}=\text{LN}\]
Then \[\Delta \text{PQR}\cong \Delta \text{LMN}\] (Read as\[\Delta \text{PQR}\]and\[\Delta LMN\]are congruent)
S-A-S Criteria
Two triangles are to be congruent if the two sides and included angle of one triangle is equal to the other.
In the above given figure \[\Delta PQR\] and \[\Delta LMN\] in such a way that
\[\text{PQ}=\text{LM},\text{ QR}=\text{MN},\text{ PR}=\text{LN}\]
Then \[\Delta \text{PQR}\cong \Delta \text{LMN}\] (Read as\[\Delta \text{PQR}\]and\[\Delta LMN\]are congruent)
S-A-S Criteria
Two triangles are to be congruent if the two sides and included angle of one triangle is equal to the other.
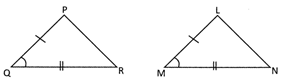 In the above given figure, \[\text{PQ}=\text{LM},\text{ QR}=\text{MN}\] and\[\angle \text{Q}=\angle \text{M}\],
Then \[\Delta \text{PQR}=\Delta \text{LMN}\]
A-S-A Criteria
If the two angles and the side included by the angles are equal to the corresponding two angles and included sides of the other triangle then the two triangles are congruent.
In the above given figure, \[\text{PQ}=\text{LM},\text{ QR}=\text{MN}\] and\[\angle \text{Q}=\angle \text{M}\],
Then \[\Delta \text{PQR}=\Delta \text{LMN}\]
A-S-A Criteria
If the two angles and the side included by the angles are equal to the corresponding two angles and included sides of the other triangle then the two triangles are congruent.
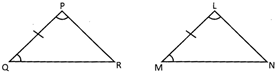 In the above given figure \[\angle P=\angle L,\angle Q=\angle M\] and \[\text{PQ}=\text{LM}\].Therefore, \[\Delta \text{PQR}\cong \Delta \text{LMN}\]
R-H-S Criteria
This criteria is for right angle triangle. If one side and hypotenuse of a right angled triangle is equal to the corresponding side and hypotenuse of other right angled triangle then two right angled triangles are said to be congruent.
In the above given figure \[\angle P=\angle L,\angle Q=\angle M\] and \[\text{PQ}=\text{LM}\].Therefore, \[\Delta \text{PQR}\cong \Delta \text{LMN}\]
R-H-S Criteria
This criteria is for right angle triangle. If one side and hypotenuse of a right angled triangle is equal to the corresponding side and hypotenuse of other right angled triangle then two right angled triangles are said to be congruent.
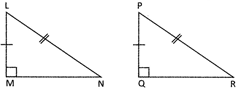 In the above given figure, LM=PQ and LN= PR, \[\angle \text{M}=\angle \text{Q}=\text{9}0{}^\circ ,\] \[\Rightarrow \] \[\Delta \text{LMN}=\Delta \text{PQR}\]
In the above given figure, LM=PQ and LN= PR, \[\angle \text{M}=\angle \text{Q}=\text{9}0{}^\circ ,\] \[\Rightarrow \] \[\Delta \text{LMN}=\Delta \text{PQR}\] 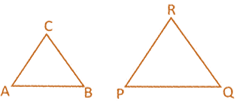 If \[\angle \text{A}=\angle \text{P},\text{ }\angle \text{B}=\angle Q\] and \[\angle C=\angle R,\] and \[\frac{AB}{PQ}=\frac{BC}{QR}=\frac{CA}{PR}\]
Then \[\Delta ABC\sim \Delta PQR\]
~ : represents similarity, and the above is read as \[\Delta \]ABC is similar to \[\Delta \text{PQR}\]
If \[\angle \text{A}=\angle \text{P},\text{ }\angle \text{B}=\angle Q\] and \[\angle C=\angle R,\] and \[\frac{AB}{PQ}=\frac{BC}{QR}=\frac{CA}{PR}\]
Then \[\Delta ABC\sim \Delta PQR\]
~ : represents similarity, and the above is read as \[\Delta \]ABC is similar to \[\Delta \text{PQR}\]
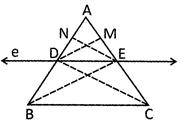 Construction:
Draw \[DM\bot AB\] and \[EN\bot AB\] and join BE, CD
Proof:
Area of \[\Delta ADE=\frac{1}{2}\times AD\times EN\] and
Area of \[\Delta BDE=\frac{1}{2}\times BD\times EN\]
Construction:
Draw \[DM\bot AB\] and \[EN\bot AB\] and join BE, CD
Proof:
Area of \[\Delta ADE=\frac{1}{2}\times AD\times EN\] and
Area of \[\Delta BDE=\frac{1}{2}\times BD\times EN\]
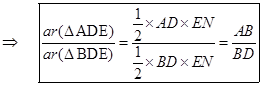 ...(i)
Similarly
...(i)
Similarly 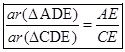 ...(ii)
But \[\Delta BDE\] and \[\Delta CDE\] have the same base DE and between same parallel lines DE and BC
\[\therefore \] \[ar(\Delta BDE)=ar(\Delta CDE)\]
\[\Rightarrow \] \[\frac{ar(\Delta ADE)}{ar(\Delta BDE)}=\frac{ar(\Delta ADE)}{ar(\Delta CDE)}\]
...(ii)
But \[\Delta BDE\] and \[\Delta CDE\] have the same base DE and between same parallel lines DE and BC
\[\therefore \] \[ar(\Delta BDE)=ar(\Delta CDE)\]
\[\Rightarrow \] \[\frac{ar(\Delta ADE)}{ar(\Delta BDE)}=\frac{ar(\Delta ADE)}{ar(\Delta CDE)}\]
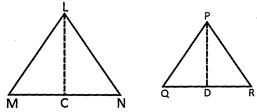 Construction:
Draw \[LC\bot MN\] and \[PD\bot QR\]
Proof:
Since \[\Delta LMN\] and \[\Delta PQD\] are similar
\[\angle \text{L}=\angle \text{P},\text{ }\angle \text{M}=\angle \text{Q},\text{ }\angle \text{N}=\angle \text{R}\]
and \[\frac{LM}{PQ}=\frac{MN}{QR}=\frac{LN}{PR}\] ... (i)
In \[\Delta \text{LMC}\] and \[\Delta \text{PQD}\], we have
\[\angle \text{LMC}=\angle \text{PQD}\]
and \[\angle \text{LCM=}\angle \text{PDQ}=\text{9}0{}^\circ \]
\[\Rightarrow \] \[\Delta \text{LMC}\tilde{\ }\Delta \text{PQD}\]
\[\Rightarrow \]\[\frac{LM}{PQ}=\frac{LC}{PD}\] ...(ii)
from (i) and (ii), we get
\[\frac{LM}{PQ}=\frac{MN}{QR}=\frac{NL}{RP}=\frac{LC}{PD}\]
Now
\[\frac{Area\,of\,\Delta LMN}{Area\,of\,\Delta PQR}=\frac{\frac{1}{{}}\times LC\times MN}{\frac{1}{\bcancel{2}}\times PD\times QR}\]
\[\Rightarrow \]\[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{LC}{PD}\times \frac{MN}{QR}\]
\[\Rightarrow \] \[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{MN}{QR}\times \frac{MN}{QR}\] \[\left[ because\frac{LC}{PD}=\frac{MN}{QR} \right]\] \[\Rightarrow \] \[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{M{{N}^{2}}}{Q{{R}^{2}}}\] more...
Construction:
Draw \[LC\bot MN\] and \[PD\bot QR\]
Proof:
Since \[\Delta LMN\] and \[\Delta PQD\] are similar
\[\angle \text{L}=\angle \text{P},\text{ }\angle \text{M}=\angle \text{Q},\text{ }\angle \text{N}=\angle \text{R}\]
and \[\frac{LM}{PQ}=\frac{MN}{QR}=\frac{LN}{PR}\] ... (i)
In \[\Delta \text{LMC}\] and \[\Delta \text{PQD}\], we have
\[\angle \text{LMC}=\angle \text{PQD}\]
and \[\angle \text{LCM=}\angle \text{PDQ}=\text{9}0{}^\circ \]
\[\Rightarrow \] \[\Delta \text{LMC}\tilde{\ }\Delta \text{PQD}\]
\[\Rightarrow \]\[\frac{LM}{PQ}=\frac{LC}{PD}\] ...(ii)
from (i) and (ii), we get
\[\frac{LM}{PQ}=\frac{MN}{QR}=\frac{NL}{RP}=\frac{LC}{PD}\]
Now
\[\frac{Area\,of\,\Delta LMN}{Area\,of\,\Delta PQR}=\frac{\frac{1}{{}}\times LC\times MN}{\frac{1}{\bcancel{2}}\times PD\times QR}\]
\[\Rightarrow \]\[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{LC}{PD}\times \frac{MN}{QR}\]
\[\Rightarrow \] \[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{MN}{QR}\times \frac{MN}{QR}\] \[\left[ because\frac{LC}{PD}=\frac{MN}{QR} \right]\] \[\Rightarrow \] \[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{M{{N}^{2}}}{Q{{R}^{2}}}\] more... 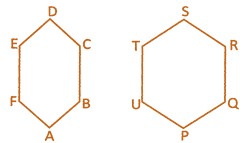 For the above two regular hexagon, they are similar if
\[\angle \text{A}=\angle \text{P}~~~~~\angle \text{B}=\angle \text{Q}\]
\[\angle \text{C}=\angle \text{R}~~~~~\angle \text{D}=\angle \text{S}\]
\[\angle \text{E}=\angle \text{T}~~~~~\angle \text{F}=\angle \text{U}\]
and
\[\frac{AB}{PQ}=\frac{BC}{QR}=\frac{CD}{RS}=\frac{DE}{ST}=\frac{EF}{TU}=\frac{FA}{UP}\]
For the above two regular hexagon, they are similar if
\[\angle \text{A}=\angle \text{P}~~~~~\angle \text{B}=\angle \text{Q}\]
\[\angle \text{C}=\angle \text{R}~~~~~\angle \text{D}=\angle \text{S}\]
\[\angle \text{E}=\angle \text{T}~~~~~\angle \text{F}=\angle \text{U}\]
and
\[\frac{AB}{PQ}=\frac{BC}{QR}=\frac{CD}{RS}=\frac{DE}{ST}=\frac{EF}{TU}=\frac{FA}{UP}\] | \[x\] | 1 | 2 | 3 |
| Y | 0 | 1 | 2 |
| \[x\] | 1 | 2 | 3 |
| Y | 6 | 4 | 2 |
 In the graph the coordinate of point of intersection is (3, 2). Therefore, \[x=3\] and y = 2 is the solution of given pair of linear equations.
In the graph the coordinate of point of intersection is (3, 2). Therefore, \[x=3\] and y = 2 is the solution of given pair of linear equations.

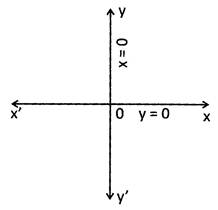 (ii) Equation of y - axis\[x=0\]
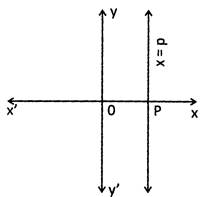
(iii) Equation of a line parallel to y - axis at a distance of p from it is \[x=p\]
(ii) Equation of y - axis\[x=0\]
(iii) Equation of a line parallel to y - axis at a distance of p from it is \[x=p\]
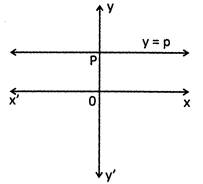
 (iv) Equation of line parallel to x - axis at a distance of p from it is y = p
(iv) Equation of line parallel to x - axis at a distance of p from it is y = p
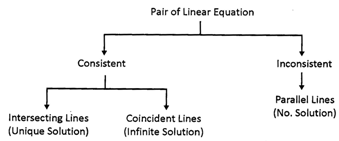
 (v) Solution of pair of linear equation in two variable. Pair of linear equation is also known as a system of two simultaneous linear equations in two variable.
The general form is
\[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\]
\[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]
If a pair of linear equation has at least one solution then it is said to be consistent. If a pair of linear equation has no solution then it is said to be inconsistent. In this topic we will emphasis on the solution of pair of linear equations by graphical method.
(v) Solution of pair of linear equation in two variable. Pair of linear equation is also known as a system of two simultaneous linear equations in two variable.
The general form is
\[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\]
\[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\]
If a pair of linear equation has at least one solution then it is said to be consistent. If a pair of linear equation has no solution then it is said to be inconsistent. In this topic we will emphasis on the solution of pair of linear equations by graphical method.
| \[x\] | |||
| \[y\] | more...


Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |