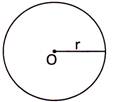
 (i) Circumference of the circle \[=2\pi r\]
(ii) Area of the circle \[=\pi {{r}^{2}}\]
(iii) Area of the semicircle \[=\frac{1}{2}\pi {{r}^{2}}\]
(iv) Perimetre of the semicircle \[=\pi r+2r\]
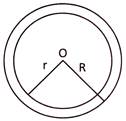
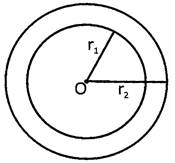
Area of Ring
Let R & r be the outer and inner radii of ring. Here area of the ring \[=\pi ({{R}^{2}}-{{r}^{2}})\]
(i) Circumference of the circle \[=2\pi r\]
(ii) Area of the circle \[=\pi {{r}^{2}}\]
(iii) Area of the semicircle \[=\frac{1}{2}\pi {{r}^{2}}\]
(iv) Perimetre of the semicircle \[=\pi r+2r\]
Area of Ring
Let R & r be the outer and inner radii of ring. Here area of the ring \[=\pi ({{R}^{2}}-{{r}^{2}})\]
 Length of Arc, Area of Sector and Segment
Let an arc AB makes an angle\[\theta <180{}^\circ \]at the center of a circle of radius r then we have:
Length of Arc, Area of Sector and Segment
Let an arc AB makes an angle\[\theta <180{}^\circ \]at the center of a circle of radius r then we have:
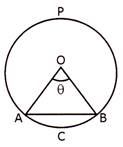 (i) Length of the arc AB\[=\frac{2\pi r\theta }{360}\]
(ii) Area of the sector OACB \[=\frac{\pi {{r}^{2}}\theta }{360}\]
(iii) Perimetre of the sector\[\text{OACB}=\text{OA}+\text{OB}+\]length of\[\overset\frown{AB}+2r+\frac{2\pi \theta }{360}\]
(iv) Area of the minor segment ACBA = (Area of the sector OACB) - (area of\[\Delta OAB\])\[=\left( \frac{\pi {{r}^{2}}\theta }{360}-\frac{1}{2}{{r}^{2}}\sin \theta \right)\]
(v) Area of the major segment BDAB = (area of the circle) - (area of the minor segment ACBA)
(i) Length of the arc AB\[=\frac{2\pi r\theta }{360}\]
(ii) Area of the sector OACB \[=\frac{\pi {{r}^{2}}\theta }{360}\]
(iii) Perimetre of the sector\[\text{OACB}=\text{OA}+\text{OB}+\]length of\[\overset\frown{AB}+2r+\frac{2\pi \theta }{360}\]
(iv) Area of the minor segment ACBA = (Area of the sector OACB) - (area of\[\Delta OAB\])\[=\left( \frac{\pi {{r}^{2}}\theta }{360}-\frac{1}{2}{{r}^{2}}\sin \theta \right)\]
(v) Area of the major segment BDAB = (area of the circle) - (area of the minor segment ACBA)
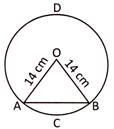 \[=\left( \frac{1}{2}\times 14\times 14\times \sin 90{}^\circ \right)=\text{98c}{{\text{m}}^{\text{2}}}=\] Area of the minor segment ACBA
= (area of the sector OACB) - (area of the \[\Delta \text{OAB}\])\[=(\text{154}-\text{98})\text{c}{{\text{m}}^{\text{2}}}=\text{56}\,\text{c}{{\text{m}}^{2}}\] Area of the major segment BDAB
= (area of the circle) - (area of the minor segment)
\[\text{=}\left\{ \left( \frac{22}{2}\times 14\times 14 \right)-56 \right\}\text{c}{{\text{m}}^{\text{2}}}=(\text{616}-\text{56})\text{c}{{\text{m}}^{\text{2}}}=\text{56}0\text{ c}{{\text{m}}^{\text{2}}}\]
\[=\left( \frac{1}{2}\times 14\times 14\times \sin 90{}^\circ \right)=\text{98c}{{\text{m}}^{\text{2}}}=\] Area of the minor segment ACBA
= (area of the sector OACB) - (area of the \[\Delta \text{OAB}\])\[=(\text{154}-\text{98})\text{c}{{\text{m}}^{\text{2}}}=\text{56}\,\text{c}{{\text{m}}^{2}}\] Area of the major segment BDAB
= (area of the circle) - (area of the minor segment)
\[\text{=}\left\{ \left( \frac{22}{2}\times 14\times 14 \right)-56 \right\}\text{c}{{\text{m}}^{\text{2}}}=(\text{616}-\text{56})\text{c}{{\text{m}}^{\text{2}}}=\text{56}0\text{ c}{{\text{m}}^{\text{2}}}\] 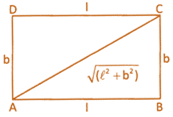 (ii) \[\text{Length}=\frac{area}{breadth},\]\[breadth=\frac{area}{length}\]
(iii) Diagonal\[=\sqrt{{{l}^{2}}+{{b}^{2}}}\]units
(iv) Perimetre\[=2(l+b)\]units
(ii) \[\text{Length}=\frac{area}{breadth},\]\[breadth=\frac{area}{length}\]
(iii) Diagonal\[=\sqrt{{{l}^{2}}+{{b}^{2}}}\]units
(iv) Perimetre\[=2(l+b)\]units
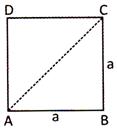 (ii) Area\[=\left\{ \frac{1}{2}{{\text{(diagonal)}}^{\text{2}}} \right\}\]sq units
(iii) Diagonal\[=a\sqrt{2}\]units
(iv) Perimetre = 4a units
(ii) Area\[=\left\{ \frac{1}{2}{{\text{(diagonal)}}^{\text{2}}} \right\}\]sq units
(iii) Diagonal\[=a\sqrt{2}\]units
(iv) Perimetre = 4a units
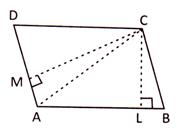
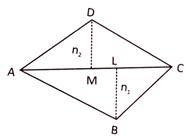 Let \[BL\bot AC\]& \[DM\bot AC\]
Then area of the quadrilateral with diagonal AC
= [(area of\[\Delta ABC\]) + (area of\[\Delta ACD\])]sq. units
\[=\left\{ \left( \frac{1}{2}\times AC\times BL \right)+\left( \frac{1}{2}\times AC\times DM \right) \right\}\]sq units
\[\therefore \]area of the quadrilateral ABCD \[=\left\{ \frac{1}{2}\times AC\times ({{h}_{1}}+{{h}_{2}}) \right\}\]sq. units
where\[{{h}_{1}}\]&\[{{h}_{2}}\] are the lengths of perpendiculars from opposite vertices to the diagonal AC.
(2) When diagonals intersect at right angles
Let ABCD be a quadrilateral whose diagonals AC and BD intersect at O at right angles then area of the quadrilateral ABCD = [(area of\[\Delta ABC\]) + (area of\[\Delta ACD\])] \[=\left( \frac{1}{2}\times AC\times BO \right)+\left( \frac{1}{2}\times AC\times OD \right)\] \[=\frac{1}{2}\times AC\times (BO+OD)\]
Let \[BL\bot AC\]& \[DM\bot AC\]
Then area of the quadrilateral with diagonal AC
= [(area of\[\Delta ABC\]) + (area of\[\Delta ACD\])]sq. units
\[=\left\{ \left( \frac{1}{2}\times AC\times BL \right)+\left( \frac{1}{2}\times AC\times DM \right) \right\}\]sq units
\[\therefore \]area of the quadrilateral ABCD \[=\left\{ \frac{1}{2}\times AC\times ({{h}_{1}}+{{h}_{2}}) \right\}\]sq. units
where\[{{h}_{1}}\]&\[{{h}_{2}}\] are the lengths of perpendiculars from opposite vertices to the diagonal AC.
(2) When diagonals intersect at right angles
Let ABCD be a quadrilateral whose diagonals AC and BD intersect at O at right angles then area of the quadrilateral ABCD = [(area of\[\Delta ABC\]) + (area of\[\Delta ACD\])] \[=\left( \frac{1}{2}\times AC\times BO \right)+\left( \frac{1}{2}\times AC\times OD \right)\] \[=\frac{1}{2}\times AC\times (BO+OD)\]
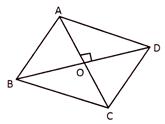 \[=\frac{1}{2}\times AC\times BD=\frac{1}{2}\times \] (product of diagonals)
\[=\frac{1}{2}\times AC\times BD=\frac{1}{2}\times \] (product of diagonals)
 \[\text{=2}\times \text{(area of }\Delta \text{ABC})\] \[\text{=}\left( \frac{1}{2}\times AB\times CL \right)\text{=(AB}\times \text{CL})=(\text{base}\times \text{height})\]
similarly if \[CM\bot AD\] then area of parallelogram\[\text{ABCD}=(\text{AD}\times \text{CM})\]\[=(\text{base}\times \] \[\text{bright})\]
\[\text{=2}\times \text{(area of }\Delta \text{ABC})\] \[\text{=}\left( \frac{1}{2}\times AB\times CL \right)\text{=(AB}\times \text{CL})=(\text{base}\times \text{height})\]
similarly if \[CM\bot AD\] then area of parallelogram\[\text{ABCD}=(\text{AD}\times \text{CM})\]\[=(\text{base}\times \] \[\text{bright})\]
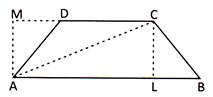 & Let\[CL\bot AB\]. Draw\[AM\bot CD\]
Let \[\text{CL}=\text{AM}=\text{h}\]
Area of trapezium ABCD = [Area of\[\Delta ABC\]+ area of\[\Delta ACD\]]
\[=\left[ \left( \frac{1}{2}\times AB\times h \right)\times \left( \frac{1}{2}\times CD\times more...
& Let\[CL\bot AB\]. Draw\[AM\bot CD\]
Let \[\text{CL}=\text{AM}=\text{h}\]
Area of trapezium ABCD = [Area of\[\Delta ABC\]+ area of\[\Delta ACD\]]
\[=\left[ \left( \frac{1}{2}\times AB\times h \right)\times \left( \frac{1}{2}\times CD\times more... 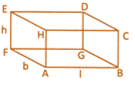 Shape of a cuboid
Shape of a cuboid
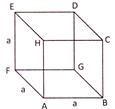 (ii) Total surface area \[=6{{a}^{2}}\]
(iii) Lateral surface area \[=4{{a}^{2}}\]
(ii) Total surface area \[=6{{a}^{2}}\]
(iii) Lateral surface area \[=4{{a}^{2}}\]
 (ii) Curved surface area \[=2\pi rh\]
(iii) Total surface area \[=(2\pi rh+2\pi {{r}^{2}})=2\pi r(h+r)\]
(ii) Curved surface area \[=2\pi rh\]
(iii) Total surface area \[=(2\pi rh+2\pi {{r}^{2}})=2\pi r(h+r)\]
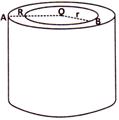 (i) Volume of material = (external volume) - (internal volume) \[=(\pi {{R}^{2}}h-\pi {{r}^{2}}h)=\pi h({{R}^{2}}-{{r}^{2}})\]
(ii) Curved surface area of hollow cylinder = (external surface area) - (internal surface area) \[=(2\pi Rh-2\pi rh)=2\pi h(R-r)\]
(iii) Total surface area of hollow cylinder = (curved surface area) + 2\[\times \](area of the base ring) \[=2\pi h(R-r)+2(\pi {{R}^{2}}-\pi {{r}^{2}})\] \[=2\pi (R-r)(R+r+h)\]
(i) Volume of material = (external volume) - (internal volume) \[=(\pi {{R}^{2}}h-\pi {{r}^{2}}h)=\pi h({{R}^{2}}-{{r}^{2}})\]
(ii) Curved surface area of hollow cylinder = (external surface area) - (internal surface area) \[=(2\pi Rh-2\pi rh)=2\pi h(R-r)\]
(iii) Total surface area of hollow cylinder = (curved surface area) + 2\[\times \](area of the base ring) \[=2\pi h(R-r)+2(\pi {{R}^{2}}-\pi {{r}^{2}})\] \[=2\pi (R-r)(R+r+h)\]
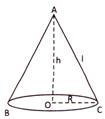 (ii) Curved surface area of the cone \[=\pi rl\]
(iii) Total surface area of the cone = (curved surface area) + (area of the base) \[\pi rl+\pi {{r}^{2}}=\] \[\pi r(l+r)\]
(ii) Curved surface area of the cone \[=\pi rl\]
(iii) Total surface area of the cone = (curved surface area) + (area of the base) \[\pi rl+\pi {{r}^{2}}=\] \[\pi r(l+r)\]
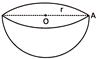
 (i) Volume of the sphere \[=\left( \frac{4}{3}\pi {{r}^{3}} \right)\]
(ii) Surface area of the sphere \[(4\pi {{r}^{2}})\]
(i) Volume of the sphere \[=\left( \frac{4}{3}\pi {{r}^{3}} \right)\]
(ii) Surface area of the sphere \[(4\pi {{r}^{2}})\]
 (i) Volume more...
(i) Volume more... 

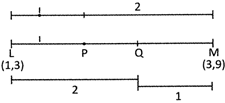 The coordinate of point P is
\[x=\frac{3\times 1+2\times 1}{3}=\frac{5}{3}\]
\[y=\frac{3\times 2+9\times 1}{3}=\frac{{{\bcancel{15}}^{3}}}{3}=5\]
The coordinate of point Q is
\[x=\frac{1\times 1+3\times 2}{3}=\frac{7}{3}\]
\[y=\frac{3\times 1+9\times 2}{3}=\frac{21}{3}=7\]
Thus the coordinate of point P is \[\left( \frac{5}{3},5 \right)\] and Q is \[\left( \frac{7}{3},7 \right)\].
The coordinate of point P is
\[x=\frac{3\times 1+2\times 1}{3}=\frac{5}{3}\]
\[y=\frac{3\times 2+9\times 1}{3}=\frac{{{\bcancel{15}}^{3}}}{3}=5\]
The coordinate of point Q is
\[x=\frac{1\times 1+3\times 2}{3}=\frac{7}{3}\]
\[y=\frac{3\times 1+9\times 2}{3}=\frac{21}{3}=7\]
Thus the coordinate of point P is \[\left( \frac{5}{3},5 \right)\] and Q is \[\left( \frac{7}{3},7 \right)\].
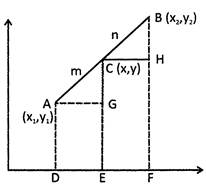 From A, B and C draw AD, BF and CE perpendicular to x - axis.
From A and C draw AG and CH perpendicular to CE and BF.
Then \[AG={{x}_{1}}-{{x}_{1}}\]
\[CH={{x}_{2}}-x\]
\[CG=y-{{y}_{1}}\]
\[BH={{y}_{2}}-y\]
\[\Delta \text{AGC}\] and \[\Delta \text{BCH}\] are similar. Therefore,
\[\frac{AG}{CH}=\frac{CG}{BH}=\frac{AC}{BC}\]
\[\Rightarrow \] \[\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{y-{{y}_{1}}}{{{y}_{2}}-y}=\frac{m}{n}\] \[\Rightarrow \] \[\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{m}{n}\] \[\Rightarrow \] \[nx-n{{x}_{1}}=m{{x}_{2}}-mx\] \[\Rightarrow \]
\[(m+n)x=m{{x}_{2}}+n{{x}_{1}}\] \[x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}\]
Similarly \[\frac{y-{{y}_{1}}}{{{y}_{2}}-y}=\frac{m}{n}\] \[\Rightarrow \] \[y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]
Thus the coordinate of point C is\[\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\]
Note: If point C is the midpoint of AB then the coordinate of C is \[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
From A, B and C draw AD, BF and CE perpendicular to x - axis.
From A and C draw AG and CH perpendicular to CE and BF.
Then \[AG={{x}_{1}}-{{x}_{1}}\]
\[CH={{x}_{2}}-x\]
\[CG=y-{{y}_{1}}\]
\[BH={{y}_{2}}-y\]
\[\Delta \text{AGC}\] and \[\Delta \text{BCH}\] are similar. Therefore,
\[\frac{AG}{CH}=\frac{CG}{BH}=\frac{AC}{BC}\]
\[\Rightarrow \] \[\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{y-{{y}_{1}}}{{{y}_{2}}-y}=\frac{m}{n}\] \[\Rightarrow \] \[\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{m}{n}\] \[\Rightarrow \] \[nx-n{{x}_{1}}=m{{x}_{2}}-mx\] \[\Rightarrow \]
\[(m+n)x=m{{x}_{2}}+n{{x}_{1}}\] \[x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}\]
Similarly \[\frac{y-{{y}_{1}}}{{{y}_{2}}-y}=\frac{m}{n}\] \[\Rightarrow \] \[y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]
Thus the coordinate of point C is\[\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\]
Note: If point C is the midpoint of AB then the coordinate of C is \[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\] 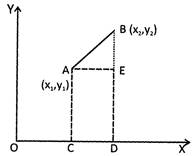 Take points A and B draws AE perpendicular to BD.
Thus \[OC={{x}_{1}},AC={{y}_{1}}\]
\[OD={{x}_{2}},BD={{y}_{2}}\]
Now \[AE={{x}_{2}}-{{x}_{1}}\] and \[BE={{y}_{2}}-{{y}_{1}}\]
In right \[\Delta \text{AEB}\]
\[\text{A}{{\text{B}}^{\text{2}}}~~=\text{A}{{\text{E}}^{\text{2}}}+\text{B}{{\text{E}}^{\text{2}}}\]
\[\Rightarrow \]\[A{{B}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}\] \[\Rightarrow \]\[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
Take points A and B draws AE perpendicular to BD.
Thus \[OC={{x}_{1}},AC={{y}_{1}}\]
\[OD={{x}_{2}},BD={{y}_{2}}\]
Now \[AE={{x}_{2}}-{{x}_{1}}\] and \[BE={{y}_{2}}-{{y}_{1}}\]
In right \[\Delta \text{AEB}\]
\[\text{A}{{\text{B}}^{\text{2}}}~~=\text{A}{{\text{E}}^{\text{2}}}+\text{B}{{\text{E}}^{\text{2}}}\]
\[\Rightarrow \]\[A{{B}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}\] \[\Rightarrow \]\[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
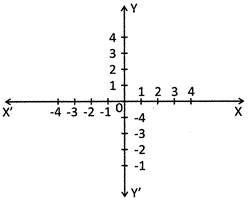 The coordinate of a point in Cartesian coordinate system is always written as ordered pair.\[(x,y)\]
i.e. \[(a,b)\ne (b,a)\]
The x - coordinate of a point is known as abscissa and y - coordinate is known as ordinate.
For a point (2, 4), 2 is abscissa and 4 is the ordinate.
The coordinate of a point in Cartesian coordinate system is always written as ordered pair.\[(x,y)\]
i.e. \[(a,b)\ne (b,a)\]
The x - coordinate of a point is known as abscissa and y - coordinate is known as ordinate.
For a point (2, 4), 2 is abscissa and 4 is the ordinate.
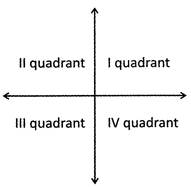 In I quadrant, \[x>0\] and \[\text{y}>0\]
In II quadrant, \[x>0\] and \[\text{y}>0\]
In III quadrant, \[x>0\] and \[\text{y}<0\]
In IV quadrant, \[x>0\] and \[\text{y}<0\]
In I quadrant, \[x>0\] and \[\text{y}>0\]
In II quadrant, \[x>0\] and \[\text{y}>0\]
In III quadrant, \[x>0\] and \[\text{y}<0\]
In IV quadrant, \[x>0\] and \[\text{y}<0\]
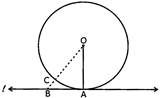 Construction:
Take a point B on line I other than A and join OB. Let OB cut the circle at the point C.
Proof:
Since O does not lies l. Therefore, the shortest distance from 0 to I will be the perpendicular so it is sufficient to prove OA is the shortest distance.
From figure
\[\text{OA}=\text{OC}\] \[\Rightarrow \] \[~\text{OA}<\text{PN}\]
OA is the shorter than any other segment joining 0 to any point on I. Hence, \[~\text{OA}\bot \ell \]
Theorem 2
The length of tangent drawn from an external point to a circle are equal.
Given: PA and PB are the tangents from point P to circle C (o, r).
To Prove: PA = PB
Construction:
Take a point B on line I other than A and join OB. Let OB cut the circle at the point C.
Proof:
Since O does not lies l. Therefore, the shortest distance from 0 to I will be the perpendicular so it is sufficient to prove OA is the shortest distance.
From figure
\[\text{OA}=\text{OC}\] \[\Rightarrow \] \[~\text{OA}<\text{PN}\]
OA is the shorter than any other segment joining 0 to any point on I. Hence, \[~\text{OA}\bot \ell \]
Theorem 2
The length of tangent drawn from an external point to a circle are equal.
Given: PA and PB are the tangents from point P to circle C (o, r).
To Prove: PA = PB
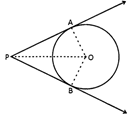 Construction:
Join PO, OA and BO
Proof:
In \[\Delta \text{POA}\] and \[\Delta \text{POB}\]
\[\text{PO}=\text{OP}\] (common)
\[\text{OA}=\text{OB}\] (radius of circle)
\[\angle \text{OAP}=\angle \text{OBP}=\text{9}0{}^\circ \]
By R.H.S Criteria
\[\Delta \text{POA}\cong \Delta \text{POB}\]
\[\frac{\text{By C}\text{.P}.\text{C}\text{.T}}{\text{PA}=\text{PB}}\]
Hence, proved
Another method:
In\[\Delta \text{POA}\]
\[P{{A}^{2}}+O{{A}^{2}}=P{{O}^{2}}\] ...(i)
In \[\Delta \text{POB}\]
\[\text{P}{{\text{B}}^{\text{2}}}+\text{O}{{\text{B}}^{\text{2}}}=\text{P}{{\text{O}}^{\text{2}}}\] ...(ii)
From (i) and (ii) we get
\[\text{P}{{\text{A}}^{\text{2}}}+\text{O}{{\text{A}}^{\text{2}}}=\text{P}{{\text{B}}^{\text{2}}}+\text{O}{{\text{B}}^{\text{2}}}\]
\[\Rightarrow \]\[\text{P}{{\text{A}}^{\text{2}}}=\text{P}{{\text{B}}^{\text{2}}}\](Since\[\text{O}{{\text{A}}^{\text{2}}}=\text{O}{{\text{B}}^{\text{2}}}\], because they are radius) \[\Rightarrow \] \[\text{PA}=\text{PB}\]
Hence, proved.
Construction:
Join PO, OA and BO
Proof:
In \[\Delta \text{POA}\] and \[\Delta \text{POB}\]
\[\text{PO}=\text{OP}\] (common)
\[\text{OA}=\text{OB}\] (radius of circle)
\[\angle \text{OAP}=\angle \text{OBP}=\text{9}0{}^\circ \]
By R.H.S Criteria
\[\Delta \text{POA}\cong \Delta \text{POB}\]
\[\frac{\text{By C}\text{.P}.\text{C}\text{.T}}{\text{PA}=\text{PB}}\]
Hence, proved
Another method:
In\[\Delta \text{POA}\]
\[P{{A}^{2}}+O{{A}^{2}}=P{{O}^{2}}\] ...(i)
In \[\Delta \text{POB}\]
\[\text{P}{{\text{B}}^{\text{2}}}+\text{O}{{\text{B}}^{\text{2}}}=\text{P}{{\text{O}}^{\text{2}}}\] ...(ii)
From (i) and (ii) we get
\[\text{P}{{\text{A}}^{\text{2}}}+\text{O}{{\text{A}}^{\text{2}}}=\text{P}{{\text{B}}^{\text{2}}}+\text{O}{{\text{B}}^{\text{2}}}\]
\[\Rightarrow \]\[\text{P}{{\text{A}}^{\text{2}}}=\text{P}{{\text{B}}^{\text{2}}}\](Since\[\text{O}{{\text{A}}^{\text{2}}}=\text{O}{{\text{B}}^{\text{2}}}\], because they are radius) \[\Rightarrow \] \[\text{PA}=\text{PB}\]
Hence, proved.


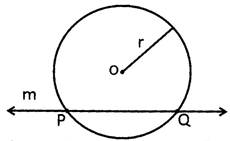 Here, line m is the secant line for circle C(0, r)
Tangent
A line which touches the circle at exactly one point is called a tangent to the circle. The point at which line touches the circle is called point of contact. Q is said to be point of contact of tangent.
Here, line m is the secant line for circle C(0, r)
Tangent
A line which touches the circle at exactly one point is called a tangent to the circle. The point at which line touches the circle is called point of contact. Q is said to be point of contact of tangent.
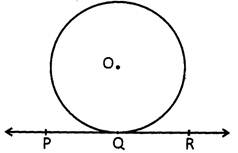 Concentric Circles
Circles are said to be concentric if and only if they have a same centre and different radius.
Concentric Circles
Circles are said to be concentric if and only if they have a same centre and different radius.
 Arc
A continuous piece of circumference of a circle is called arc.
Arc
A continuous piece of circumference of a circle is called arc.
 Here, PQ is arc of C(o, r).
Concurrent Arc
Two arc are said to be concurrent if they subtend same angle at the centre.
Here, PQ is arc of C(o, r).
Concurrent Arc
Two arc are said to be concurrent if they subtend same angle at the centre.
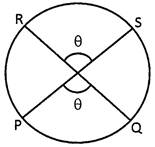 Minor and Major Arcs
If the length of an arc is less then the arc of a semicircle then it is called minor arc and which is greater than the semicircles is called major arc. arc \[\overset\frown{PRQ}\] is minor arc and \[\overset\frown{PSQ}\] is major arc
Minor and Major Arcs
If the length of an arc is less then the arc of a semicircle then it is called minor arc and which is greater than the semicircles is called major arc. arc \[\overset\frown{PRQ}\] is minor arc and \[\overset\frown{PSQ}\] is major arc
 Segment
The region bounded by chord and an arc is called segment. The segment which contains minor arc is called minor segment and which contains major arc is called major segment.
Segment
The region bounded by chord and an arc is called segment. The segment which contains minor arc is called minor segment and which contains major arc is called major segment.
 Congruent Circles
Two circles are said to be congruent if they have same radii.
Important Properties
Congruent Circles
Two circles are said to be congruent if they have same radii.
Important Properties
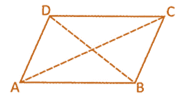 In the above given figure,
\[\text{ar(}\Delta \text{ABC})=\text{ar}(\Delta \text{ACD)}\]
Similarly
\[\text{ar(}\Delta \text{ABD})=\text{ar}(\Delta \text{BCD)}\]
(ii) Parallelograms which are on the same base and between the same parallel lines are equal in area.
In the above given figure,
\[\text{ar(}\Delta \text{ABC})=\text{ar}(\Delta \text{ACD)}\]
Similarly
\[\text{ar(}\Delta \text{ABD})=\text{ar}(\Delta \text{BCD)}\]
(ii) Parallelograms which are on the same base and between the same parallel lines are equal in area.
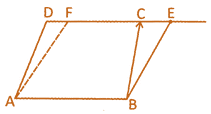 In the above given figure,
\[ar(l{{l}^{gm}}ABCD)=ar(l{{l}^{gm}}ABEF)\]
(iii) Triangles which are on the same base and between the same parallel lines are equal in area.
In the above given figure,
\[ar(l{{l}^{gm}}ABCD)=ar(l{{l}^{gm}}ABEF)\]
(iii) Triangles which are on the same base and between the same parallel lines are equal in area.
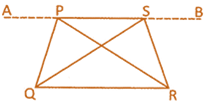 In the above given figure \[QR|\,\,|AB\]
Then \[~\text{ar(}\Delta \text{PQR)}=\text{ar(}\Delta \text{QRS)}\]
(iv) Area of trapezium= \[\frac{1}{2}\] (sum of parallel sides) \[\times \] (distance between them)
In the above given figure \[QR|\,\,|AB\]
Then \[~\text{ar(}\Delta \text{PQR)}=\text{ar(}\Delta \text{QRS)}\]
(iv) Area of trapezium= \[\frac{1}{2}\] (sum of parallel sides) \[\times \] (distance between them)


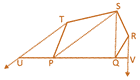 (a) ar(pentagon PQRST) \[=\text{ar(}\Delta \text{STU)}+\text{ar(}\Delta \text{QRV)}\]
(b) ar(pentagon PQRST) \[~=\text{ar(}\Delta \text{SUV)}\]
(c) ar(pentagon PQRST) \[~=\text{ar(}\Delta \text{SUV)}+\text{ar(}\Delta \text{TUP)}\]
(d) ar(pentagon PQRST) \[=\text{ar}(\Delta \text{SUV})+\text{ar(}\Delta \text{QRV)}\]
(e) None of these
Answer: (b)
Explanation:
Since \[RV|\,|SQ\] \[\Rightarrow \] \[~\text{ar(}\Delta \text{SPT)}=\text{ar}(\Delta \text{TUP)}\]
\[\text{ar(}\Delta \text{SQR)}+\text{ar(}\Delta \text{SPT)}+\text{ar(}\Delta \text{SPQ)}=\text{ar(}\Delta \text{SRV)}+\]\[\text{ar(}\Delta \text{SUP)}+\text{ar(}\Delta \text{BPQ)}\]
\[\Rightarrow \] \[\text{ar(pentagon PQRST)}=\text{ar(}\Delta \text{SUV)}\]
(a) ar(pentagon PQRST) \[=\text{ar(}\Delta \text{STU)}+\text{ar(}\Delta \text{QRV)}\]
(b) ar(pentagon PQRST) \[~=\text{ar(}\Delta \text{SUV)}\]
(c) ar(pentagon PQRST) \[~=\text{ar(}\Delta \text{SUV)}+\text{ar(}\Delta \text{TUP)}\]
(d) ar(pentagon PQRST) \[=\text{ar}(\Delta \text{SUV})+\text{ar(}\Delta \text{QRV)}\]
(e) None of these
Answer: (b)
Explanation:
Since \[RV|\,|SQ\] \[\Rightarrow \] \[~\text{ar(}\Delta \text{SPT)}=\text{ar}(\Delta \text{TUP)}\]
\[\text{ar(}\Delta \text{SQR)}+\text{ar(}\Delta \text{SPT)}+\text{ar(}\Delta \text{SPQ)}=\text{ar(}\Delta \text{SRV)}+\]\[\text{ar(}\Delta \text{SUP)}+\text{ar(}\Delta \text{BPQ)}\]
\[\Rightarrow \] \[\text{ar(pentagon PQRST)}=\text{ar(}\Delta \text{SUV)}\]
You need to login to perform this action.
You will be redirected in
3 sec
