question_answer 1)
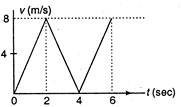
The v-t graph for a particle is as shown. The distance travelled in the first four seconds is
A)
12 m
done
clear
B)
16 m
done
clear
C)
20 m
done
clear
D)
24 m
done
clear
View Answer play_arrow
question_answer 2) If a convex lens of focal length 75 cm and a concave lens of focal length 50 cm are combined together, what will be their resulting power?
A)
\[-6.6D\]
done
clear
B)
\[+0.66\text{ }D\]
done
clear
C)
\[+6.6D\]
done
clear
D)
\[-0.66D\]
done
clear
View Answer play_arrow
question_answer 3) When a ferromagnetic material is heated to temperature above its curie point, the material
A)
is permanently magnetized
done
clear
B)
remains ferromagnetic
done
clear
C)
behaves like a diamagnetic material
done
clear
D)
behaves like a paramagnetic material
done
clear
View Answer play_arrow
question_answer 4) Light of energy 2.0 eV falls on a metal of work function 1.4 eV. The stopping potential is
A)
0.6 V
done
clear
B)
2.0 V
done
clear
C)
3.4 V
done
clear
D)
1.4 V
done
clear
View Answer play_arrow
question_answer 5) During an isothermal expansion of an ideal gas
A)
its internal energy decreases
done
clear
B)
its internal energy does not change
done
clear
C)
the work done by the gas is equal to the quantity of heat absorbed by it
done
clear
D)
both (b) and (c) are correct
done
clear
View Answer play_arrow
question_answer 6) Find the dimensions of electric permittivity
A)
\[[{{A}^{2}}{{M}^{-1}}{{L}^{-3}}{{T}^{4}}]\]
done
clear
B)
\[[{{A}^{2}}{{M}^{-1}}{{L}^{3}}{{T}^{0}}]\]
done
clear
C)
\[[A{{M}^{-1}}{{L}^{-3}}{{T}^{4}}]\]
done
clear
D)
\[[{{A}^{2}}{{M}^{0}}{{L}^{-3}}{{T}^{4}}]\]
done
clear
View Answer play_arrow
question_answer 7) In Youngs double slit experiment, the slits are 3 mm apart. The wavelength of light used is \[5000\text{ }\overset{o}{\mathop{\text{A}}}\,\]and the distance between the slits and the screen is 90 cm. The fringe width in mm is
A)
1.5
done
clear
B)
0.015
done
clear
C)
2.0
done
clear
D)
0.15
done
clear
View Answer play_arrow
question_answer 8) A moving coil galvanometer has a resistance of\[10\text{ }\Omega \]. and full scale deflection of 0.01 A. It can be converted into voltmeter of 10 V full scale by connecting into resistance of
A)
\[\text{9}\text{.90 }\Omega \] in series
done
clear
B)
\[\text{10 }\Omega \] in series
done
clear
C)
\[\text{990 }\Omega \] in series
done
clear
D)
\[\text{0}\text{.10 }\Omega \] in series
done
clear
View Answer play_arrow
question_answer 9) A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity vq. We consider a point A on the surface of the disc. Then the acceleration of the point A is
A)
constant in magnitude as well as direction
done
clear
B)
constant in direction
done
clear
C)
constant in magnitude
done
clear
D)
constant
done
clear
View Answer play_arrow
question_answer 10) The number of free electrons per 100 mm of ordinary Copper wire is\[2\times {{10}^{21}}\]. Average drift speed of electrons is 0.25 mm/s. The current flowing is
A)
5 A
done
clear
B)
80 A
done
clear
C)
8 A
done
clear
D)
0.8 A
done
clear
View Answer play_arrow
question_answer 11) A Carnot engine whose low temperature reservoir is at\[7{}^\circ C\] has an efficiency of 50%. It is desired to increase the efficiency to 70%. By how many degrees should the temperature of the high temperature reservoir be increased?
A)
840 K
done
clear
B)
280 K
done
clear
C)
560 K
done
clear
D)
380 K
done
clear
View Answer play_arrow
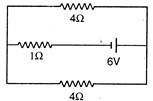
question_answer 12)
The current in the\[1\,\Omega \]. resistor shown in the circuit is
A)
\[\frac{2}{3}A\]
done
clear
B)
\[3A\]
done
clear
C)
\[6\text{ }A\]
done
clear
D)
\[\text{2 }A\]
done
clear
View Answer play_arrow
question_answer 13) Water is flowing through a pipe of constant cross-section. At some point the pipe becomes narrow and the cross-section is halved. The speed of water is
A)
reduced to zero
done
clear
B)
decreased by a factor of 2
done
clear
C)
increased by a factor of 2
done
clear
D)
unchanged
done
clear
View Answer play_arrow
question_answer 14) In Millikans oil drop experiment, an oil drop of mass\[16\times {{10}^{-6}}kg\]is balanced by an electric field of\[{{10}^{6}}V/m\]. The charge in coulomb on the drop is (assuming\[g=10m/{{s}^{2}}\])
A)
\[6.2\times {{10}^{-11}}\]
done
clear
B)
\[16\times {{10}^{-9}}\]
done
clear
C)
\[16\times {{10}^{-11}}\]
done
clear
D)
\[16\times {{10}^{-13}}\]
done
clear
View Answer play_arrow
question_answer 15) The minimum wavelength of X-ray emitted from X-ray machine operating at an accelerating potential of V volts is
A)
\[\frac{hc}{eV}\]
done
clear
B)
\[\frac{Vc}{eh}\]
done
clear
C)
\[\frac{eh}{Vc}\]
done
clear
D)
\[\frac{eV}{hc}\]
done
clear
View Answer play_arrow
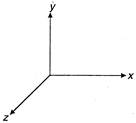
question_answer 16)
Light wave is travelling alongy-direction. If the corresponding E vector at any time is along the \[x-\]axis, the direction of B vector at that time is along
A)
\[y-\]axis
done
clear
B)
\[x-\]axis
done
clear
C)
\[+z\]axis
done
clear
D)
\[-z-\]axis
done
clear
View Answer play_arrow
question_answer 17) Two plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. The angle between the two mirrors is
A)
\[30{}^\circ \]
done
clear
B)
\[45{}^\circ \]
done
clear
C)
\[60{}^\circ \]
done
clear
D)
\[75{}^\circ \]
done
clear
View Answer play_arrow
question_answer 18) A radioactive material has a half-life of 8 yr. The activity of the material will decrease to about 1/8 of its original value in
A)
256 yr
done
clear
B)
128 yr
done
clear
C)
64 yr
done
clear
D)
24 yr
done
clear
View Answer play_arrow
question_answer 19) The number of beats produced per second by two vibrations\[{{x}_{1}}={{x}_{0}}\]and\[{{x}_{2}}={{x}_{0}}\sin 652\pi t\]is
A)
2
done
clear
B)
3
done
clear
C)
4
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 20) An engine is supposed to operate between two reservoirs at temperature\[727{}^\circ C\]and\[227{}^\circ C\]. The maximum possible efficiency of such an engine is
A)
1/2
done
clear
B)
¼
done
clear
C)
3/4
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 21) A string vibrates according to the equation\[y=5\sin \left( \frac{2\pi x}{3} \right)\cos 20\pi t\]where\[x\]and y are in cm and t in second. The distance between two adjacent nodes is
A)
3 cm
done
clear
B)
4.5 cm
done
clear
C)
6 cm
done
clear
D)
1.5 cm
done
clear
View Answer play_arrow
question_answer 22) On Centigrade scale the temperature of a body increases by\[30{}^\circ \]. The increase in temperature on Fahrenheit scale is
A)
\[50{}^\circ \]
done
clear
B)
\[40{}^\circ \]
done
clear
C)
\[30{}^\circ \]
done
clear
D)
\[54{}^\circ \]
done
clear
View Answer play_arrow
question_answer 23) A particle performs uniform circular motion with an angular momentum L. If the frequency of particles motion is doubled and its KE is halved. the angular momentum becomes
A)
\[\frac{L}{2}\]
done
clear
B)
\[2L\]
done
clear
C)
\[4L\]
done
clear
D)
\[\frac{L}{4}\]
done
clear
View Answer play_arrow
question_answer 24) An electron initially at rest is accelerated through a potential difference of\[1V\]. The energy acquired by electron is
A)
\[{{10}^{-19}}J\]
done
clear
B)
\[1.6\times {{10}^{-19}}erg\]
done
clear
C)
\[1.6\times {{10}^{-19}}J\]
done
clear
D)
\[1J\]
done
clear
View Answer play_arrow
question_answer 25) A nucleus decays by\[{{\beta }^{+}}-\] emission followed by a\[\gamma -\]emission. If the atomic and mass numbers of the parent nucleus are Z and A respectively, the corresponding numbers for the daughter nucleus are respectively
A)
\[Z-1\]and\[A-1\]
done
clear
B)
\[Z+1\] and A
done
clear
C)
\[Z-1\]and A
done
clear
D)
\[Z+1\]and\[A-1\]
done
clear
View Answer play_arrow
question_answer 26) An iron bar of length 10 m is heated from\[0{}^\circ C\] to\[100{}^\circ C\]. If the coefficient of linear thermal expansion of iron is\[10\times {{10}^{-6}}/{}^\circ C,\] the increase in the length of bar is
A)
0.5 cm
done
clear
B)
1.0 cm
done
clear
C)
1.5 cm
done
clear
D)
2:0 cm
done
clear
View Answer play_arrow
question_answer 27) A balloon going upward with a velocity of 12 m/s is at a height of 65 m from the earths surface at any instant. Exactly at this instant a ball drops from it. How much time will the ball take in reaching the surface of earth? \[(g=10m/{{s}^{2}})\]
A)
5s
done
clear
B)
5 s
done
clear
C)
10s
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 28) A block moving on a surface with velocity 20 m/s comes to rest because of surface friction over a distance of 40 m. Taking\[(g=10m/{{s}^{2}})\], the coefficient of dynamic friction is
A)
0.5
done
clear
B)
0.3
done
clear
C)
0.2
done
clear
D)
0.1
done
clear
View Answer play_arrow
question_answer 29) A dielectric slab is inserted between the plates of an isolated charged capacitor. Which of the following quantities remain unchanged?
A)
The charge on the capacitor
done
clear
B)
The stored energy in the capacitor
done
clear
C)
The potential difference between the plates
done
clear
D)
The electric field in the capacitor
done
clear
View Answer play_arrow
question_answer 30) In a medium of dielectric constant K, the electric field is\[\overrightarrow{E}\]. If\[{{\varepsilon }_{0}}\]is permittivity of the free space, the electric displacement vector is
A)
\[\frac{K\vec{E}}{{{\varepsilon }_{0}}}\]
done
clear
B)
\[\frac{{\vec{E}}}{K{{\varepsilon }_{0}}}\]
done
clear
C)
\[\frac{{{\varepsilon }_{0}}\vec{E}}{K}\]
done
clear
D)
\[K{{\varepsilon }_{0}}\vec{E}\]
done
clear
View Answer play_arrow
question_answer 31) The phenomenon of polarization of light indicates that
A)
light is a longitudinal wave
done
clear
B)
light is a transverse wave
done
clear
C)
light is not a wave
done
clear
D)
light travels with the velocity of\[3\times {{10}^{8}}m/s\]
done
clear
View Answer play_arrow
question_answer 32) A ray of light passes from vacuum into a medium of refractive index u., the angle of incidence is found to be twice the angle of refraction. Then the angle of incidence is
A)
\[2{{\cos }^{-1}}\left( \frac{\mu }{2} \right)\]
done
clear
B)
\[{{\sin }^{-1}}\left( \mu \right)\]
done
clear
C)
\[{{\sin }^{-1}}\left( \frac{\mu }{2} \right)\]
done
clear
D)
\[{{\cos }^{-1}}\left( \frac{\mu }{2} \right)\]
done
clear
View Answer play_arrow
question_answer 33) A body dropped from top of a tower fall through 60 m during the last two seconds of its fall. The height of tower is\[(g=10\text{ }m/{{s}^{2}})\]
A)
95 m
done
clear
B)
60 m
done
clear
C)
80 m
done
clear
D)
90 m
done
clear
View Answer play_arrow
question_answer 34) A compound microscope has an eyepiece of focal length 10 cm and an objective of focal length 4 cm. Calculate the magnification, if an object is kept at a distance of 5 cm from the objective, so that final image is formed at the least distance of distinct vision 20 cm.
A)
12
done
clear
B)
11
done
clear
C)
10
done
clear
D)
13
done
clear
View Answer play_arrow
question_answer 35) The ratio of the velocity of sound in oxygen to that in hydrogen at same temperature and pressure is approximately
A)
\[16:1\]
done
clear
B)
\[1:16\]
done
clear
C)
\[4:1\]
done
clear
D)
\[1:4\]
done
clear
View Answer play_arrow
question_answer 36) The ratio\[\frac{g}{{{g}_{h}}},\]where g and\[{{g}_{h}}\]are the accelerations due to gravity at the surface of the earth and at a height h above the earths surface respectively, is
A)
\[{{\left( 1+\frac{h}{R} \right)}^{2}}\]
done
clear
B)
\[{{\left( 1+\frac{R}{h} \right)}^{2}}\]
done
clear
C)
\[{{\left( \frac{R}{h} \right)}^{2}}\]
done
clear
D)
\[{{\left( \frac{h}{R} \right)}^{2}}\]
done
clear
View Answer play_arrow
question_answer 37) In order that the light reflected from the surface of a medium of refractive index a is plane polarized, the angle of incidence should be
A)
\[{{\sin }^{-1}}(\mu )\]
done
clear
B)
\[{{\tan }^{-1}}(\mu )\]
done
clear
C)
\[{{\cot }^{-1}}(\mu )\]
done
clear
D)
\[{{\tan }^{-1}}\left( \frac{1}{\mu } \right)\]
done
clear
View Answer play_arrow
question_answer 38) The magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be
A)
\[\frac{B}{4}\]
done
clear
B)
\[\frac{B}{2}\]
done
clear
C)
2B
done
clear
D)
4B
done
clear
View Answer play_arrow
question_answer 39) Let V be the electric potential at a given point. Then the electric field\[{{E}_{x}}\]along\[x-\]direction at that point is given by
A)
\[\int_{0}^{\infty }{V}dx\]
done
clear
B)
\[\frac{dV}{dx}\]
done
clear
C)
\[-\frac{dV}{dx}\]
done
clear
D)
\[-V\frac{dV}{dx}\]
done
clear
View Answer play_arrow
question_answer 40) Potential at any point inside a charged hollow, sphere
A)
increases with distance
done
clear
B)
is a constant
done
clear
C)
decreases with distance from centre
done
clear
D)
is zero
done
clear
View Answer play_arrow
question_answer 41) The length of a simple pendulum is increased by 44 %. What is the percentage increase in its time period?
A)
10%
done
clear
B)
20%
done
clear
C)
40 %
done
clear
D)
44 %
done
clear
View Answer play_arrow
question_answer 42) Four charges\[{{q}_{1}}=2\times {{10}^{-8}}C,{{q}_{2}}=-2\times {{10}^{-8}}C,\]\[{{q}_{3}}=-3\times {{10}^{-8}}C\]and\[{{q}_{4}}=6\times {{10}^{-8}}C\]are placed at four comers of a square of side\[\sqrt{2}m\]. What is the potential at the centre of the square?
A)
270V
done
clear
B)
300V
done
clear
C)
Zero
done
clear
D)
100 V
done
clear
View Answer play_arrow
question_answer 43) A point charge + q is placed at the midpoint of a cube of side L. The electric flux emerging from the cube is
A)
\[\frac{q}{{{\varepsilon }_{0}}}\]
done
clear
B)
\[\frac{q}{6{{L}^{2}}{{\varepsilon }_{0}}}\]
done
clear
C)
\[\frac{6q{{L}^{2}}}{{{\varepsilon }_{0}}}\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 44) In which of the following is the interference due to the division of wavefront?
A)
Youngs double slit experiment
done
clear
B)
Fresnels biprism experiment
done
clear
C)
Llyods mirror experiment
done
clear
D)
Demonstration colours of thin film
done
clear
View Answer play_arrow
question_answer 45) A source of sound of frequency 500 Hz is moving towards a stationary observer with velocity 30 m/s. The speed of sound is 330 m/s. The frequency heard by the observer will be
A)
545 Hz
done
clear
B)
580 Hz
done
clear
C)
458.3 Hz
done
clear
D)
550 Hz
done
clear
View Answer play_arrow
question_answer 46) A ball is hit at\[45{}^\circ \]to the horizontal with a kinetic energy\[{{E}_{k}}\]. The kinetic energy at the highest point is
A)
\[{{E}_{k}}\]
done
clear
B)
\[\frac{{{E}_{k}}}{2}\]
done
clear
C)
\[\frac{{{E}_{k}}}{\sqrt{2}}\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 47) In stream line flow of liquid, the total energy of liquid is constant at
A)
all points
done
clear
B)
inner points
done
clear
C)
outer points
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 48) The magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current\[I\]is
A)
\[\frac{{{\mu }_{0}}I}{\pi L}\]
done
clear
B)
\[\frac{2{{\mu }_{0}}I}{\pi L}\]
done
clear
C)
\[\frac{\sqrt{2}{{\mu }_{0}}I}{\pi L}\]
done
clear
D)
\[\frac{2\sqrt{2}{{\mu }_{0}}I}{\pi L}\]
done
clear
View Answer play_arrow
question_answer 49) Two thin lenses of focal lengths\[{{f}_{1}}\]and\[{{f}_{2}}\]are placed in contact with each other. The focal length of the combination is
A)
\[\frac{{{f}_{1}}+{{f}_{2}}}{2}\]
done
clear
B)
\[\sqrt{{{f}_{1}}}{{f}_{2}}\]
done
clear
C)
\[\frac{{{f}_{1}}{{f}_{2}}}{{{f}_{1}}+{{f}_{2}}}\]
done
clear
D)
\[\frac{{{f}_{1}}{{f}_{2}}}{{{f}_{1}}-{{f}_{2}}}\]
done
clear
View Answer play_arrow
question_answer 50) For ionising an excited hydrogen atom, the energy required (in eV) will be
A)
a little less than 13.6
done
clear
B)
13.6
done
clear
C)
more than 13.6
done
clear
D)
3.4 or less
done
clear
View Answer play_arrow
question_answer 51) A hollow sphere of charge does not produce an electric field at any
A)
interior point
done
clear
B)
outer point
done
clear
C)
beyond 2 m
done
clear
D)
beyond 10 m
done
clear
View Answer play_arrow
question_answer 52) When a force of 0.1 N is applied, the spring is stretched by 1.5 cm. The spring is cut into three parts and one part is stretched by 3 cm. Find the force required for doing so
A)
0.2 N
done
clear
B)
0.3 N
done
clear
C)
0.4 N
done
clear
D)
0.6 N
done
clear
View Answer play_arrow
question_answer 53) A bomb at rest explodes into 3 parts of the same mass. The momentum of the 2 parts is \[-2p\hat{i}\]and\[p\hat{j}\]. The momentum of the third part will have a magnitude of
A)
\[P\]
done
clear
B)
\[\sqrt{3p}\]
done
clear
C)
\[p\sqrt{5}\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 54) A couple produces a
A)
pure linear motion
done
clear
B)
pure rotational
done
clear
C)
no motion
done
clear
D)
both linear (a) and (b)
done
clear
View Answer play_arrow
question_answer 55) If the external forces acting on a system have zero resultant, the centre of mass
A)
may move but not accelerate
done
clear
B)
may accelerate
done
clear
C)
must not move
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 56) In the reaction \[R-C\equiv N+4(H)\xrightarrow[{}]{X}RC{{H}_{2}}N{{H}_{2}}\]\[X\]can be
A)
\[LiAl{{H}_{4}}\]
done
clear
B)
\[{{H}_{2}}S{{O}_{4}}\]
done
clear
C)
\[Ni\]
done
clear
D)
\[2KBr\]
done
clear
View Answer play_arrow
question_answer 57) At a given temperature the equilibrium constant for the reaction of\[PC{{l}_{5}}PC{{l}_{3}}+C{{l}_{2}}\]is\[2.4\times {{10}^{-3}}\]. At the same temperature, the equilibrium constant for the reaction\[PC{{l}_{3}}(g)+C{{l}_{2}}(g)PC{{l}_{5}}(g)\]is
A)
\[2.4\times {{10}^{-3}}\]
done
clear
B)
\[-2.4\times {{10}^{-3}}\]
done
clear
C)
\[4.2\times {{10}^{2}}\]
done
clear
D)
\[4.8\times {{10}^{-2}}\]
done
clear
View Answer play_arrow
question_answer 58) Which of the following is called polyamide?
A)
Terylene
done
clear
B)
Rayon
done
clear
C)
Nylon
done
clear
D)
Orion
done
clear
View Answer play_arrow
question_answer 59) The number of electrons in the valence shell of sulphur in\[S{{F}_{6}}\]is
A)
12
done
clear
B)
10
done
clear
C)
8
done
clear
D)
11
done
clear
View Answer play_arrow
question_answer 60) The minimum energy required for the reacting molecules to undergo reaction is
A)
potential energy
done
clear
B)
kinetic energy
done
clear
C)
thermal energy
done
clear
D)
activation energy
done
clear
View Answer play_arrow
question_answer 61) Which of the following is correct for the reaction? \[{{N}_{2}}(g)+3{{H}_{2}}(g)2N{{H}_{3}}(g)\]
A)
\[{{K}_{p}}={{K}_{c}}\]
done
clear
B)
\[{{K}_{p}}<{{K}_{c}}\]
done
clear
C)
\[{{K}_{p}}>{{K}_{c}}\]
done
clear
D)
Pressure is required to predict the correlation
done
clear
View Answer play_arrow
question_answer 62) The rate constant of a first order reaction is\[6.9\times {{10}^{-3}}{{s}^{-1}}\]. How much time will it take to reduce the initial concentration to its 1/8th value?
A)
100s
done
clear
B)
200s
done
clear
C)
300s
done
clear
D)
400s
done
clear
View Answer play_arrow
question_answer 63) Which has the minimum freezing point?
A)
One molal\[NaCl\]aqueous solution
done
clear
B)
One molal\[CaCla\]aqueous solution
done
clear
C)
One molal\[KCl\]aqueous solution
done
clear
D)
One molal urea aqueous solution
done
clear
View Answer play_arrow
question_answer 64) Among the following, the most acidic is
A)
\[C{{H}_{3}}COOH\]
done
clear
B)
\[ClC{{H}_{2}}COOH\]
done
clear
C)
\[C{{l}_{2}}CHCOOH\]
done
clear
D)
\[C{{l}_{2}}CHC{{H}_{2}}COOH\]
done
clear
View Answer play_arrow
question_answer 65) For a Bohr atom angular momentum M of the electron is: (n = 0, 1, 2, ......)
A)
\[\frac{n{{h}^{2}}}{4\pi }\]
done
clear
B)
\[\frac{{{n}^{2}}{{h}^{2}}}{4\pi }\]
done
clear
C)
\[\frac{\sqrt{n{{h}^{2}}}}{4\pi }\]
done
clear
D)
\[\frac{nh}{2\pi }\]
done
clear
View Answer play_arrow
question_answer 66) Which of the following combination will form an electrovalent bond?
A)
P and\[Cl\]
done
clear
B)
\[N{{H}_{3}}\]and\[B{{F}_{3}}\]
done
clear
C)
H and \[Ca\]
done
clear
D)
H and \[S\]
done
clear
View Answer play_arrow
question_answer 67) How many moles of\[A{{l}_{2}}{{(S{{O}_{4}})}_{3}}\]would be in 50 g of the substance?
A)
0.083 mol
done
clear
B)
0.952 mol
done
clear
C)
0.481 mol
done
clear
D)
0.140 mol
done
clear
View Answer play_arrow
question_answer 68) The IUPAC name of the compound \[C{{H}_{3}}CONHBr\]is
A)
1-bromoacetamide
done
clear
B)
ethanoylbromide
done
clear
C)
N-bromoethanamide
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 69) Which of the following is a condensation polymer?
A)
\[-\left[ N{{H}_{2}}-\overset{\begin{smallmatrix} O \\ |\,| \end{smallmatrix}}{\mathop{C}}\,-{{(C{{H}_{2}})}_{5}} \right]{{-}_{n}}\]
done
clear
B)
Rubber
done
clear
C)
Polyvinyl chloride
done
clear
D)
Polyethylene
done
clear
View Answer play_arrow
question_answer 70) The solubility of\[Ca{{F}_{2}}\]in pure water is\[2.3\times {{10}^{-4}}mol\text{ }d{{m}^{-3}}\]. Its solubility product will be
A)
\[4.6\times {{10}^{-4}}\]
done
clear
B)
\[4.6\times {{10}^{-8}}\]
done
clear
C)
\[6.9\times {{10}^{-12}}\]
done
clear
D)
\[4.9\times {{10}^{-11}}\]
done
clear
View Answer play_arrow
question_answer 71) Copper sulphate solution, when added to an excess of ammonium hydroxide, forms a complex compound due to
A)
\[{{[Cu{{(N{{H}_{3}})}_{2}}]}^{2+}}\]
done
clear
B)
\[{{[Cu{{(N{{H}_{3}})}_{4}}]}^{2+}}\]
done
clear
C)
\[{{[Cu{{(N{{H}_{3}})}_{6}}]}^{2+}}\]
done
clear
D)
\[C{{u}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 72) If a solution containing 0.072 g atom of sulphur in 100 g of a solvent\[({{k}_{f}}=7.0)\]gave a freezing point depression of\[0.84{}^\circ C,\]the molecular formula of sulphur in the solutions is
A)
\[{{S}_{6}}\]
done
clear
B)
\[{{S}_{7}}\]
done
clear
C)
\[{{S}_{8}}\]
done
clear
D)
\[{{S}_{9}}\]
done
clear
View Answer play_arrow
question_answer 73) Which of the following is a dynamic isomerism?
A)
Metamerism
done
clear
B)
Geometrical isomerism
done
clear
C)
Tautomerism
done
clear
D)
Co-ordinate isomerism
done
clear
View Answer play_arrow
question_answer 74) When\[{{K}_{2}}C{{r}_{2}}{{O}_{7}}\]is converted into\[{{K}_{2}}Cr{{O}_{4}},\]the change in oxidation number of chromium is
A)
0
done
clear
B)
5
done
clear
C)
7
done
clear
D)
9
done
clear
View Answer play_arrow
question_answer 75) Which of the following will be the most effective in the coagulation of\[Fe{{(OH)}_{3}}\]Sol?
A)
\[KCN\]
done
clear
B)
\[BaC{{l}_{2}}\]
done
clear
C)
\[NaCl\]
done
clear
D)
\[M{{g}_{3}}{{(P{{O}_{4}})}_{2}}\]
done
clear
View Answer play_arrow
question_answer 76) For d-block elements the first ionization potential is of the order
A)
\[Zn>Fe>Cu>Cr\]
done
clear
B)
\[Sc=Ti<V=Cr\]
done
clear
C)
\[Zn<Cu<Ni<Co\]
done
clear
D)
\[V>Cr>Mn>Fe\]
done
clear
View Answer play_arrow
question_answer 77) High basicity of IV^NH relative to\[M{{e}_{3}}N\]is attributed to
A)
effect of solvent
done
clear
B)
inductive effect of Me
done
clear
C)
shape of \[M{{e}_{2}}NH\]
done
clear
D)
shape of\[M{{e}_{3}}N\]
done
clear
View Answer play_arrow
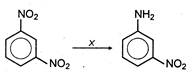
question_answer 78)
In the reaction
A)
\[SiC\]
done
clear
B)
\[{{H}_{2}}S{{O}_{4}}\]
done
clear
C)
\[KMn{{O}_{4}}\]
done
clear
D)
\[Fe/HCl\]
done
clear
View Answer play_arrow
question_answer 79) In Grignard reagent the carbon-magnesium bond is
A)
electrovalent
done
clear
B)
covalent
done
clear
C)
dative
done
clear
D)
hydrogen bonding
done
clear
View Answer play_arrow
question_answer 80) The radius of hydrogen atom in the ground state is\[0.53\text{ }\overset{o}{\mathop{\text{A}}}\,\]. The radius of\[L{{i}^{2+}}\]ion (atomic number = 3) in a similar state is
A)
\[0.176\text{ }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
\[\text{0}\text{.30 }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
\[\text{0}\text{.53 }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
\[\text{1}\text{.23 }\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 81) Tyndall effect shown by colloids is due to
A)
scattering of light by the particles
done
clear
B)
movements of particles
done
clear
C)
reflection of light by the particles
done
clear
D)
coagulation of particles
done
clear
View Answer play_arrow
question_answer 82) Iodine is a
A)
electrovalent solid
done
clear
B)
atomic solid
done
clear
C)
molecular solid
done
clear
D)
covalent solid
done
clear
View Answer play_arrow
question_answer 83) \[F{{e}^{2+}}\]ion is distinguished from\[F{{e}^{3+}}\]ion by
A)
\[BaC{{l}_{2}}\]
done
clear
B)
\[KCN\]
done
clear
C)
\[NaN{{O}_{3}}\]
done
clear
D)
\[N{{H}_{4}}SCN\]
done
clear
View Answer play_arrow
question_answer 84) Lattice energy of a solid increases if
A)
size of ions is small
done
clear
B)
charges of ions are small
done
clear
C)
ions are neutral
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 85) Which of the following will not give a positive iodoform test?
A)
\[C{{H}_{3}}C{{H}_{2}}CHOHC{{H}_{3}}\]
done
clear
B)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}COC{{H}_{3}}\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}COC{{H}_{2}}C{{H}_{3}}\]
done
clear
D)
\[C{{H}_{3}}CO{{C}_{6}}{{H}_{5}}\]
done
clear
View Answer play_arrow
question_answer 86) The reason for the loss of optical activity of lactic acid when\[-OH\]group is changed by H is that
A)
chiral centre of the molecule is destroyed
done
clear
B)
molecules acquires asymmetry
done
clear
C)
due to change in configuration
done
clear
D)
structural changes occurs
done
clear
View Answer play_arrow
question_answer 87) To distinguish between salicylic acid and phenol one can use
A)
\[NaHC{{O}_{3}}\]solution
done
clear
B)
\[5%\text{ }NaOH\]solution
done
clear
C)
neutral\[FeC{{l}_{3}}\]
done
clear
D)
bromine water
done
clear
View Answer play_arrow
question_answer 88) \[C-H\]bond energy is about 101 kcal/mol for methane, ethane and other alkanes but is only 77 kcal/mol for\[C-H\]bond of\[C{{H}_{3}}\]in toluene. This is because
A)
of inductive effect due to\[-C{{H}_{3}}\]in toluene
done
clear
B)
of the presence of benzene ring in toluene
done
clear
C)
of resonance among the structures of benzyl radical in toluene
done
clear
D)
aromaticity of toluene
done
clear
View Answer play_arrow
question_answer 89) Which of the following ions can be replaced by \[{{H}^{+}}\]ions when\[{{H}_{2}}\]gas is bubbled through the solutions containing these ions?
A)
\[L{{i}^{+}}\]
done
clear
B)
\[B{{a}^{2+}}\]
done
clear
C)
\[C{{u}^{2+}}\]
done
clear
D)
\[B{{e}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 90) Alum is added to muddy water because
A)
it acts as disinfectant
done
clear
B)
it results in coagulation of clay arid sand
done
clear
C)
clay is soluble in alum, hence removes it
done
clear
D)
it makes water alkaline which is good for health
done
clear
View Answer play_arrow
question_answer 91) \[N{{H}_{3}}\]gas is dried over
A)
\[CaO\]
done
clear
B)
\[HN{{O}_{3}}\]
done
clear
C)
\[{{P}_{2}}{{O}_{5}}\]
done
clear
D)
\[CuS{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 92) Which one of the following is not correct for an ideal solution?
A)
It must obey Raoults law
done
clear
B)
\[\Delta H=0\]
done
clear
C)
\[\Delta U=0\]
done
clear
D)
\[\Delta H=\Delta V\ne 0\]
done
clear
View Answer play_arrow
question_answer 93) Borax bead test of Cr (chromium) is
A)
green
done
clear
B)
blue
done
clear
C)
violet
done
clear
D)
brown
done
clear
View Answer play_arrow
question_answer 94) A catalyst
A)
lowers the activation energy
done
clear
B)
changes the rate constant
done
clear
C)
changes the product
done
clear
D)
itself destroys in the reaction
done
clear
View Answer play_arrow
question_answer 95) Which of the following is cross-linked polymer?
A)
Teflon
done
clear
B)
Orion
done
clear
C)
Nylon
done
clear
D)
Bakelite
done
clear
View Answer play_arrow
question_answer 96) In the reaction sequence\[C{{H}_{3}}CH=C{{H}_{2}}\xrightarrow[(ii){{H}_{2}}O/Zn]{(i){{O}_{3}}}\Pr oducts\]Products will be
A)
\[C{{H}_{3}}COC{{H}_{3}}\]
done
clear
B)
\[C{{H}_{3}}COC{{H}_{2}}OH\]
done
clear
C)
\[C{{H}_{3}}COOH+HCOOH\]
done
clear
D)
\[C{{H}_{3}}CHO+HCHO\]
done
clear
View Answer play_arrow
question_answer 97) The conditions for aromaticity is
A)
molecule must have clouds of delocalized \[\pi -\]electrons
done
clear
B)
molecule must contain\[(4n+2)\pi -\]electrons
done
clear
C)
both (a) and (b)
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 98) Which of the following increases the octane number?
A)
Branching of chain
done
clear
B)
Absence of double and triple bond
done
clear
C)
Non-cyclic alkanes
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 99) Chlorobenzene gives aniline with
A)
\[N{{H}_{3}}/C{{u}_{2}}O\]
done
clear
B)
\[N{{H}_{3}}/{{H}_{2}}S{{O}_{4}}\]
done
clear
C)
\[NaN{{H}_{2}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 100) In\[CsCl\] type structure the co-ordination of\[C{{s}^{+}}\]and\[C{{l}^{-}}\]are
A)
6, 6
done
clear
B)
6, 8
done
clear
C)
8, 8
done
clear
D)
8, 6
done
clear
View Answer play_arrow
question_answer 101) Hesss law is used to calculate:
A)
enthalpy of reaction
done
clear
B)
entropy of reaction
done
clear
C)
work done in reaction
done
clear
D)
all of the above
done
clear
View Answer play_arrow
question_answer 102) Which of the following is not a Lewis base?
A)
\[N{{H}_{3}}\]
done
clear
B)
\[{{H}_{2}}O\]
done
clear
C)
\[AlC{{l}_{3}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 103) Active charcoal is a good catalyst because
A)
made up of carbon atoms
done
clear
B)
is very reactive
done
clear
C)
has more adsorption power
done
clear
D)
has inert nature toward reagent
done
clear
View Answer play_arrow
question_answer 104) \[{{H}_{2}}\]cannot be displaced by
A)
\[L{{i}^{+}}\]
done
clear
B)
\[S{{r}^{2+}}\]
done
clear
C)
\[A{{l}^{3+}}\]
done
clear
D)
\[A{{g}^{+}}\]
done
clear
View Answer play_arrow
question_answer 105) Which of the following is amphoteric?
A)
\[{{V}_{2}}{{O}_{3}}\]
done
clear
B)
\[CuO\]
done
clear
C)
\[{{V}_{2}}{{O}_{5}}\]
done
clear
D)
\[NiO\]
done
clear
View Answer play_arrow
question_answer 106) The emf of the cell,\[({{E}_{Z{{n}^{2+}}/Zn}}=-0.76\,V)\]\[Zn/Z{{n}^{2+}}(1M)||C{{u}^{2+}}(1M)Cu\]\[({{E}_{C{{u}^{2+}}/Cu}}=+0.34V)\]will be
A)
\[+1.10\text{ }V\]
done
clear
B)
\[-1.10\text{ }V\]
done
clear
C)
\[+\text{ }0.42V\]
done
clear
D)
\[-0.42V\]
done
clear
View Answer play_arrow
question_answer 107) Which of the following is correct number of carbon atom present as the constituent of kerosene oil?
A)
\[{{C}_{10}}-{{C}_{16}}\]
done
clear
B)
\[{{C}_{4}}-{{C}_{6}}\]
done
clear
C)
\[{{C}_{8}}-{{C}_{16}}\]
done
clear
D)
\[{{C}_{12}}-{{C}_{18}}\]
done
clear
View Answer play_arrow
question_answer 108) Water possesses a high dielectric constant, therefore
A)
it always contains ions
done
clear
B)
it is a universal solvent
done
clear
C)
can dissolve covalent compounds
done
clear
D)
can conduct electricity
done
clear
View Answer play_arrow
question_answer 109) Aldehydes can be oxidised by
A)
Tollens reagent
done
clear
B)
Fehling solution
done
clear
C)
Benedict solution
done
clear
D)
All of these
done
clear
View Answer play_arrow
question_answer 110) The\[\Delta H_{f}^{o}\]for\[C{{O}_{2}}(g),CO(g)\]and\[{{H}_{2}}O(g)\] are \[-393.5,-110.5\] and \[-241.8~kJ/mol\] respectively. The standard enthalpy change (in kJ) for the reaction\[C{{O}_{2}}(g)+{{H}_{2}}(g)\xrightarrow[{}]{{}}CO(g)+{{H}_{2}}O(g)\]is
A)
524.1
done
clear
B)
41.2
done
clear
C)
\[-262.5\]
done
clear
D)
\[-41.2\]
done
clear
View Answer play_arrow
question_answer 111) Of a total of 600 bolts, 20% are too large and 10% are too small. The remainder are considered to be suitable. If a bolt is selected at random, the probability that it will be suitable is
A)
\[\frac{1}{5}\]
done
clear
B)
\[\frac{7}{10}\]
done
clear
C)
\[\frac{1}{10}\]
done
clear
D)
\[\frac{3}{10}\]
done
clear
View Answer play_arrow
question_answer 112) The area enclosed within the curve\[|x|+|y|=1\]is
A)
1 sq unit
done
clear
B)
\[2\sqrt{2}\]sq unit
done
clear
C)
\[\sqrt{2}\]sq unit
done
clear
D)
2 sq unit
done
clear
View Answer play_arrow
question_answer 113) If\[P(B)=\frac{3}{4},P(A\cap B\cap \overline{C})=\frac{1}{3}\]and\[P(\overline{A}\cap B\cap \overline{C})=\frac{1}{3},\]then\[P(B\cap C)\]is
A)
1/12
done
clear
B)
1/6
done
clear
C)
1/15
done
clear
D)
1/9
done
clear
View Answer play_arrow
question_answer 114) The value of\[\sin \left( {{\sin }^{-1}}\frac{1}{3}+{{\sec }^{-1}}3 \right)+\]\[\cos \left( {{\tan }^{-1}}\frac{1}{2}+{{\tan }^{-1}}2 \right)\]is
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 115) \[\int_{0}^{\pi /2}{\frac{\sqrt{\cot x}}{\sqrt{\cot x}+\sqrt{\tan x}}}dx\]is equal to
A)
1
done
clear
B)
\[-1\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\frac{\pi }{4}\]
done
clear
View Answer play_arrow
question_answer 116) Area bounded by the curve\[y={{\log }_{e}}x,x=0,y\le 0\]and\[x-\]axis is
A)
1 sq unit
done
clear
B)
1/2 sq unit
done
clear
C)
2 sq unit
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 117) If\[|\overrightarrow{a}\times \overrightarrow{b}{{|}^{2}}+|\overrightarrow{a}.\overrightarrow{b}{{|}^{2}}=144\]and\[|\overrightarrow{a}|=4,\]Then\[|\overrightarrow{b}|\]is equal to
A)
12
done
clear
B)
3
done
clear
C)
8
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 118) Given that\[|\overrightarrow{a}|=3,|\overrightarrow{b}|=4,|\overrightarrow{a}\times \overrightarrow{b}|=10,\]then\[|\overrightarrow{a}.\overrightarrow{b}{{|}^{2}}\]equals
A)
88
done
clear
B)
44
done
clear
C)
22
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 119) \[\underset{x\to 0}{\mathop{\lim }}\,x\log \sin x\]is equal to
A)
zero
done
clear
B)
\[\infty \]
done
clear
C)
1
done
clear
D)
cannot be determined
done
clear
View Answer play_arrow
question_answer 120) If\[x=1+a+{{a}^{2}}+......\] to infinity and \[y=1+b+{{b}^{2}}+......\]to infinity, where a, bare proper fractions, then\[1+ab+{{a}^{2}}{{b}^{2}}+...\]to infinity is equal to
A)
\[\frac{xy}{x+y-1}\]
done
clear
B)
\[\frac{xy}{x-y-1}\]
done
clear
C)
\[\frac{xy}{x-y+1}\]
done
clear
D)
\[\frac{xy}{x+y+1}\]
done
clear
View Answer play_arrow
question_answer 121) \[{{\cos }^{4}}\theta -{{\sin }^{4}}\theta \]is equal to
A)
\[1+2{{\sin }^{2}}\left( \frac{\theta }{2} \right)\]
done
clear
B)
\[2{{\cos }^{2}}\theta -1\]
done
clear
C)
\[1-2{{\sin }^{2}}\left( \frac{\theta }{2} \right)\]
done
clear
D)
\[1+2{{\cos }^{2}}\theta \]
done
clear
View Answer play_arrow
question_answer 122) If\[y=f(x)=\frac{x+2}{x-1},\]then
A)
\[x=f(y)\]
done
clear
B)
\[f(1)=3\]
done
clear
C)
\[y\]increases with\[x\]for\[x<1\]
done
clear
D)
\[f\]is a rational function of\[x\]
done
clear
View Answer play_arrow
question_answer 123) A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is \[60{}^\circ \]. When he retreats 20 ft from the bank, he finds the angle to be\[30{}^\circ \]. The breadth of the river in feet is
A)
15
done
clear
B)
\[15\sqrt{3}\]
done
clear
C)
\[10\sqrt{3}\]
done
clear
D)
\[10\]
done
clear
View Answer play_arrow
question_answer 124) If\[\tan \alpha =\frac{m}{m+1}\]and\[\tan \beta =\frac{1}{2m+1},\]then\[\alpha +\beta \]is equal to
A)
\[\frac{\pi }{3}\]
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
zero
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 125) If\[f(x)=x[\sqrt{x}-\sqrt{x+1}],\]then
A)
\[f(x)\]is continuous but not differentiable at\[x=0\]
done
clear
B)
\[f(x)\]is not differentiable at \[x=0\]
done
clear
C)
\[f(x)\]is differentiable at\[x=0\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 126) \[tan\alpha +2\text{ }tan\text{ }2\alpha +4\text{ }tan\text{ }4\alpha +8\text{ }cot\text{ }8\alpha \]is equal to
A)
\[tan\text{ }16\alpha \]
done
clear
B)
0
done
clear
C)
\[\cot \alpha \]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 127) A book contains 1000 pages numbered consecutively. The probability that the sum of the digits of the number of a page is 9, is
A)
zero
done
clear
B)
\[\frac{55}{1000}\]
done
clear
C)
\[\frac{33}{1000}\]
done
clear
D)
\[\frac{44}{1000}\]
done
clear
View Answer play_arrow
question_answer 128) A number is chosen at random among the first 120 natural numbers. The probability of the number chosen being a multiple of 5 or 15 is
A)
\[\frac{1}{8}\]
done
clear
B)
\[\frac{1}{5}\]
done
clear
C)
\[\frac{1}{24}\]
done
clear
D)
\[\frac{1}{6}\]
done
clear
View Answer play_arrow
question_answer 129) If\[\overrightarrow{a}=2\hat{i}+\hat{j}+\hat{k},\overrightarrow{b}=\hat{i}-2\hat{j}-\hat{k},\]\[\overrightarrow{c}=\hat{i}+\hat{j}+\hat{k},\] then\[\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})\]equals
A)
\[5\hat{i}-7\hat{j}-3\hat{k}\]
done
clear
B)
\[5\hat{i}+7\hat{j}-3\hat{k}\]
done
clear
C)
\[5\hat{i}-7\hat{j}+3\hat{k}\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 130) The coefficient of\[{{x}^{4}}\]in the expansion of\[{{\left( \frac{x}{2}-\frac{3}{{{x}^{2}}} \right)}^{10}}\]is
A)
\[\frac{504}{259}\]
done
clear
B)
\[\frac{450}{263}\]
done
clear
C)
\[\frac{405}{256}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 131) Equation of the ellipse whose foci are (2, 2) and (4, 2) and the major axis is of length 10, is
A)
\[\frac{{{(x+3)}^{2}}}{24}+\frac{{{(y+2)}^{2}}}{25}=1\]
done
clear
B)
\[\frac{{{(x-3)}^{2}}}{24}+\frac{{{(y-2)}^{2}}}{25}=1\]
done
clear
C)
\[\frac{{{(x+3)}^{2}}}{24}+\frac{{{(y+2)}^{2}}}{24}=1\]
done
clear
D)
\[\frac{{{(x-3)}^{2}}}{25}+\frac{{{(y-2)}^{2}}}{24}=1\]
done
clear
View Answer play_arrow
question_answer 132) The volume of the solid generated by the revolution of the curve\[y=\frac{{{a}^{3}}}{{{a}^{2}}+{{x}^{2}}}\]about\[x-\]axis is
A)
\[\frac{1}{2}{{\pi }^{3}}{{a}^{2}}\]
done
clear
B)
\[{{\pi }^{3}}{{a}^{2}}\]
done
clear
C)
\[\frac{1}{2}{{\pi }^{2}}{{a}^{3}}\]
done
clear
D)
\[{{\pi }^{2}}{{a}^{3}}\]
done
clear
View Answer play_arrow
question_answer 133) The radius of the circle\[\left| \frac{z-i}{z+i} \right|=5\]is given by
A)
\[\frac{13}{12}\]
done
clear
B)
\[\frac{5}{12}\]
done
clear
C)
5
done
clear
D)
625
done
clear
View Answer play_arrow
question_answer 134) If\[\overrightarrow{a}=(1,p,1),\overrightarrow{b}=(q,2,2),\overrightarrow{a}.\overrightarrow{b}=r\]and \[\overrightarrow{a}\times \overrightarrow{b}=(0,-3,3)\], then p, q, r are in that order
A)
1, 5, 9
done
clear
B)
9, 5, 1
done
clear
C)
5, 1, 9
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 135) The foci of an ellipse are\[(0,\pm 4)\]and the equations for the directories are\[y=\pm 9\]. The equation for the ellipse is
A)
\[5{{x}^{2}}+9{{y}^{2}}=4\]
done
clear
B)
\[2{{x}^{2}}-6{{y}^{2}}=28\]
done
clear
C)
\[6{{x}^{2}}+3{{y}^{2}}=45\]
done
clear
D)
\[9{{x}^{2}}+5{{y}^{2}}=180\]
done
clear
View Answer play_arrow
question_answer 136) The straight lines \[x+y=0,3x+y-4=0\] and \[x+3y-4=0\]form a triangle which is
A)
right angled
done
clear
B)
equilateral
done
clear
C)
isosceles
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 137) The eccentricity of the hyperbola \[9{{x}^{2}}-16{{y}^{2}}-18x-64y-199=0\]is
A)
\[\frac{16}{9}\]
done
clear
B)
\[\frac{5}{4}\]
done
clear
C)
\[\frac{25}{16}\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 138) A four-digit number is formed by the digits 1, 2, 3, 4 with no repetition. The probability that the number is odd, is
A)
zero
done
clear
B)
1/3
done
clear
C)
1/4
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 139) The coefficient of\[{{x}^{n}}\]in the expansion of\[\frac{(a-bx)}{{{e}^{x}}}\]is
A)
\[\frac{{{(-1)}^{n}}}{n!}(a+bn)\]
done
clear
B)
\[\frac{{{(-1)}^{n}}}{n!}(b+an)\]
done
clear
C)
\[\frac{{{(-1)}^{n+1}}}{n!}(a+bn)\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 140) The value of \[{{\cot }^{-1}}9+\cos e{{c}^{-1}}\frac{\sqrt{41}}{4}\]is given by
A)
0
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
\[{{\tan }^{-1}}2\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 141) The value of \[\underset{x\to 0}{\mathop{\lim }}\,\frac{{{e}^{x}}+\log (1+x)-{{(1-x)}^{-2}}}{{{x}^{2}}}\]is equal to
A)
0
done
clear
B)
-3
done
clear
C)
\[-1\]
done
clear
D)
infinity
done
clear
View Answer play_arrow
question_answer 142) The values of k for which the equations \[{{x}^{2}}-kx-21=0\]and\[{{x}^{2}}-3kx+35=0\]will have a common roots are
A)
\[k=\pm 4\]
done
clear
B)
\[k=\pm 1\]
done
clear
C)
\[k=\pm 3\]
done
clear
D)
\[k=0\]
done
clear
View Answer play_arrow
question_answer 143) \[\overrightarrow{a}\]and\[\overrightarrow{b}\]are two non-zero vectors, then \[(\overrightarrow{a}+\overrightarrow{b})-(\overrightarrow{a}-\overrightarrow{b})\]is equal to
A)
\[a+b\]
done
clear
B)
\[{{(a-b)}^{2}}\]
done
clear
C)
\[{{(a+b)}^{2}}\]
done
clear
D)
\[({{a}^{2}}-{{b}^{2}})\]
done
clear
View Answer play_arrow
question_answer 144) If\[sin\text{ }x+si{{n}^{2}}x=1,\]then \[co{{s}^{6}}x+co{{s}^{12}}x+3\text{ }co{{s}^{10}}x+3\text{ }co{{s}^{8}}x\] is equal to
A)
1
done
clear
B)
\[co{{s}^{3}}x\text{ }si{{n}^{3}}x\]
done
clear
C)
0
done
clear
D)
\[\infty \]
done
clear
View Answer play_arrow
question_answer 145) The integrating factor of the differential equation\[\frac{dy}{dx}+\frac{1}{x}y=3x\]is
A)
\[x\]
done
clear
B)
In \[x\]
done
clear
C)
0
done
clear
D)
\[\infty \]
done
clear
View Answer play_arrow
question_answer 146) \[\int_{0}^{\pi /2}{x{{\sin }^{2}}x{{\cos }^{2}}x}dx\]is equal to
A)
\[\frac{{{\pi }^{2}}}{32}\]
done
clear
B)
\[\frac{{{\pi }^{2}}}{16}\]
done
clear
C)
\[\frac{\pi }{32}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 147) If H is harmonic mean between P and Q, then the value of\[\frac{H}{P}+\frac{H}{Q}\]is
A)
2
done
clear
B)
\[\frac{PQ}{(P+Q)}\]
done
clear
C)
\[\frac{(P+Q)}{PQ}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 148) The value of y for which the equation \[{{x}^{2}}+pxy+{{y}^{2}}-5x-7y+6=0\]represents a pair of straight lines is
A)
5/2
done
clear
B)
5
done
clear
C)
2
done
clear
D)
2/5
done
clear
View Answer play_arrow
question_answer 149) Angle between the vectors\[\sqrt{3}(\overrightarrow{a}\times \overrightarrow{b})\]and\[\overrightarrow{b}-(\overrightarrow{a}.\overrightarrow{b})\overrightarrow{a}\]is
A)
\[\frac{\pi }{2}\]
done
clear
B)
0
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[\frac{\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 150) The equation of the circle passing through (4,5) having the centre (2, 2) is
A)
\[{{x}^{2}}+{{y}^{2}}+4x+4y-5=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-4x-4y-5=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-4x=13\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-4x-4y+5=0\]
done
clear
View Answer play_arrow
question_answer 151) The smallest positive integer n for which\[{{\left( \frac{1+i}{1-i} \right)}^{n}}=1\]is
A)
\[n=8\]
done
clear
B)
\[n=12\]
done
clear
C)
\[n=16\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 152) The equation of tangents drawn from the origin to the circle \[{{x}^{2}}+{{y}^{2}}-2rx-2hy+{{h}^{2}}=0\] are
A)
\[x=0,y=0\]
done
clear
B)
\[x=1,y=0\]
done
clear
C)
\[({{h}^{2}}-{{r}^{2}}))x-2rhy=0,y=0\]
done
clear
D)
\[({{h}^{2}}-{{r}^{2}})x-2rhy=0,x=0\]
done
clear
View Answer play_arrow
question_answer 153) The value of\[{{9}^{1/3}}\times {{9}^{1/9}}\times {{9}^{1/27}}\times ....\infty \]is
A)
9
done
clear
B)
1
done
clear
C)
3
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 154) Let\[0<P(A)<1,0<P(B)<1\]and\[P(A\cup B)=P(A)+P(B)-P(A)\text{ }P(B),\]then
A)
\[P(B/A)=P(B)-P(A)\]
done
clear
B)
\[P(A\cup B)=P(A)+P(B)\]
done
clear
C)
\[P(A\cap B)=P(A)P(B)\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 155) The probability that in the toss of two dice we obtain the sum 7 or 11, is
A)
\[\frac{1}{6}\]
done
clear
B)
\[\frac{1}{18}\]
done
clear
C)
\[\frac{2}{9}\]
done
clear
D)
\[\frac{23}{108}\]
done
clear
View Answer play_arrow
question_answer 156) If\[{{2}^{x}}+{{2}^{y}}={{2}^{x+y}},\]then\[\frac{dy}{dx}\]is equal to
A)
\[\frac{({{2}^{x}}+{{2}^{y}})}{({{2}^{x}}-{{2}^{y}})}\]
done
clear
B)
\[\frac{({{2}^{x}}+{{2}^{y}})}{(1+{{2}^{x+y}})}\]
done
clear
C)
\[{{2}^{x-y}}\left( \frac{{{2}^{y}}-1}{1-{{2}^{x}}} \right)\]
done
clear
D)
\[\frac{{{2}^{x+y}}-{{2}^{x}}}{{{2}^{y}}}\]
done
clear
View Answer play_arrow
question_answer 157) If the probability of A to fail in an examination is 0.2 and that for B is 0.3, then probability that either A or B is fail, is
A)
0.5
done
clear
B)
0.44
done
clear
C)
0.8
done
clear
D)
0.25
done
clear
View Answer play_arrow
question_answer 158) If\[f(x)=\cos (\log x),\]then\[f(x)f(y)-\frac{1}{2}\left[ f\left( \frac{x}{y} \right)+f(xy) \right]\]has the value
A)
\[-1\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[-2\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 159) If\[y={{3}^{x-1}}+{{3}^{-x-1}}\] (\[x\]real), then the least value of y is
A)
2
done
clear
B)
6
done
clear
C)
2/3
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 160) The value of\[\theta \]lying between\[\theta =0\]and\[\frac{\pi }{2}\]and satisfying the equation\[\left| \begin{matrix} 1+{{\sin }^{2}}\theta & {{\cos }^{2}}\theta & 4\sin 4\theta \\ {{\sin }^{2}}\theta & 1+{{\cos }^{2}}\theta & 4\sin 4\theta \\ {{\sin }^{2}}\theta & {{\cos }^{2}}\theta & 1+4\sin 4\theta \\ \end{matrix} \right|=0\]is
A)
\[\frac{7\pi }{24}\]
done
clear
B)
\[\frac{5\pi }{24}\]
done
clear
C)
\[\frac{11\pi }{2}\]
done
clear
D)
\[\frac{\pi }{24}\]
done
clear
View Answer play_arrow
question_answer 161) \[{{\left( \frac{-1+\sqrt{-3}}{2} \right)}^{100}}+{{\left( \frac{-1-\sqrt{-3}}{2} \right)}^{100}}\]is equal to
A)
2
done
clear
B)
zero
done
clear
C)
\[-1\]
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 162) If\[\alpha ,\beta \]be the two roots of the equation \[{{x}^{2}}+x+1=0,\]then the equation whose roots are \[\frac{\alpha }{\beta }\]and \[\frac{\beta }{\alpha }\]is
A)
\[{{x}^{2}}+x+1=0\]
done
clear
B)
\[{{x}^{2}}-x+1=0\]
done
clear
C)
\[{{x}^{2}}-x-1=0\]
done
clear
D)
\[{{x}^{2}}+x-1=0\]
done
clear
View Answer play_arrow
question_answer 163) In a binomial distribution, the mean is 4 and variance is 3. Then, its mode is
A)
5
done
clear
B)
6
done
clear
C)
4
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 164) The equation of a line passing through\[(-2,-4)\] and perpendicular to the line\[3x-y+5=0\]is
A)
\[3y+x-8=0\]
done
clear
B)
\[3x+y+6=0\]
done
clear
C)
\[x+3y+14=0\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 165) \[\underset{x\to 0}{\mathop{\lim }}\,{{(\cos ecx)}^{1/\log x}}\]is equal to
A)
0
done
clear
B)
1
done
clear
C)
1/e
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 166) The minimum value of \[f(x)={{\sin }^{4}}x+{{\cos }^{4}}x,0\le x\le \frac{\pi }{2}\]is
A)
\[\frac{1}{2\sqrt{2}}\]
done
clear
B)
\[\frac{1}{4}\]
done
clear
C)
\[\frac{-1}{2}\]
done
clear
D)
\[\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 167) A vector of magnitude 5 and perpendicular to. \[(\hat{i}-2\hat{j}+\hat{k})\]and\[(2\hat{i}+\hat{j}-3\hat{k})\]is
A)
\[\frac{5\sqrt{3}}{3}(\hat{i}+\hat{j}+\hat{k})\]
done
clear
B)
\[\frac{5\sqrt{3}}{3}(\hat{i}+\hat{j}-\hat{k})\]
done
clear
C)
\[\frac{5\sqrt{3}}{3}(\hat{i}-\hat{j}+\hat{k})\]
done
clear
D)
\[\frac{5\sqrt{3}}{3}(-\hat{i}+\hat{j}+\hat{k})\]
done
clear
View Answer play_arrow
question_answer 168) \[\int_{-\pi /3}^{\pi /3}{\frac{x\sin x}{{{\cos }^{2}}x}}dx\]is
A)
\[\frac{1}{3}(4\pi +1)\]
done
clear
B)
\[\frac{4\pi }{3}-2\log \tan \frac{5\pi }{12}\]
done
clear
C)
\[\frac{4\pi }{3}+\log \tan \frac{5}{12}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 169) \[\sum\limits_{r=0}^{m}{^{n+r}{{C}_{n}}}\]is equal to
A)
\[^{n+m+1}{{C}_{n+1}}\]
done
clear
B)
\[^{n+m+2}{{C}_{n}}\]
done
clear
C)
\[^{n+m+3}{{C}_{n-1}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 170) The angle between the lines \[2x=3y=-\text{ }z\] and \[6x=-\text{ }y=-4z\]is
A)
\[90{}^\circ \]
done
clear
B)
\[0{}^\circ \]
done
clear
C)
\[30{}^\circ \]
done
clear
D)
\[45{}^\circ \]
done
clear
View Answer play_arrow
 \[X\]is
\[X\]is
