
The value of an Algebraic Expression
Step 1: If possible simplify the given algebraic expression.
Step 2: Replace variable with given numerical value.
Step 3: Simplify it.

Find the value of \[\frac{{{x}^{3}}+{{y}^{3}}+{{z}^{3}}-3xyz}{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-xy-yz-zx},\] lf \[x=1,y=2\] and \[z=-1.\]
(a) 24
(b) 14
(c) 7
(d) 2
(e) None of these
Answer: (d)
Explanation
\[\frac{{{x}^{3}}+{{y}^{3}}+{{z}^{3}}-3xyz}{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-xy-yz-zx}=\frac{(x+y+z+)({{x}^{2}}+{{y}^{2}}+{{z}^{2}}-xy-yz-zx)}{({{x}^{2}}+{{y}^{2}}+{{z}^{2}}-xy-yz-zx)}\]
\[=(x+y+z).\] Now putting the values of \[x,\text{ }y\]and \[z\] we get = 2


Find the value of \[4\text{ }xy\text{(}x-y\text{)}-6{{x}^{2}}\text{(}y-{{y}^{2}}\text{)}-3{{y}^{2}}(2{{x}^{2}}-x)+2xy(x-y)\] for \[x=5\]and \[y=13.\]
(a) - 195
(b) 2535
(c) - 2535
(d) 215
(e) None of these
Answer: (c)
Explanation
\[4xy(x-y)-6{{x}^{2}}(y-{{y}^{2}})-3{{y}^{2}}(2{{x}^{2}}-x)+2xy(x-y)\]\[4{{x}^{2}}y-4x{{y}^{2}}-6{{x}^{2}}y+6{{x}^{2}}{{y}^{2}}-6{{y}^{2}}{{x}^{2}}+3x{{y}^{2}}+2{{x}^{2}}y-2x{{y}^{2}}\]
After simplification, we get \[-\text{ }3x{{y}^{2}}=-3\times 5\times 13\times 13=-2535\]

The value of A, B, C, D, E, F, G, H and I for which \[(ABC)\times (DEF)=GHI\]
(a) (6, 5, 7, 8, 2, 6, 1, 8, 4, 0)
(b) (7, 9, 5, 2, 6, 4, 8, 4, 0)
(c) (4, 6, 7, 8, 5, 7, 0, 8, 9)
(d) (1, 0, 3, 7, 8, 4, 2, 1, 0)
(e) None of these
Answer: (d)
Explanation
If we put the value of A, B, C, D, E, F, G, H and I from option D in the left hand side and right hand side of given expression, then it becomes zero.

Find the value of \[3{{x}^{3}}y+4{{x}^{y}}+2{{y}^{x}},\] if \[x=2\]\[x=2\]and \[y=-2.\]
(a) - 39
(b) 39
(c) 13
(d) Cannot be determined
(e) None of these
Answer: (a)

Find the value of \[{{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-bc-ca,\]if \[a=2b=-2\]and \[c=1.\]
(a) 12
(b) 1
(c) 13
(d) 7
(e) None of these
Answer: (d)

Which one of the following options is the correct value or the expression \[\frac{axy+byz+cxy}{ax+by+cz+1},\] if \[a=1,b=2,c=-1,x=-1,y=2,z=3?\]
(a) 12
(b) 10
(c) 13
(d) 11
(e) None of these
Answer: (a)
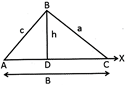 The vertices of a triangle are denoted by the Capital letters of English alphabets.
In the above figure \[\Delta ABC,\]the sides are AB, BC and CA.
The vertices of a triangle are denoted by the Capital letters of English alphabets.
In the above figure \[\Delta ABC,\]the sides are AB, BC and CA.
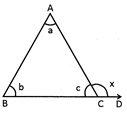 Proof: In \[\Delta ABC,a+b+c=180{}^\circ \]
but,\[c+x=180{}^\circ \] (Linear pair) \[c={{180}^{0}}-x\]
Putting "c" in the above equation, we get
\[a+b+180{}^\circ -x=180{}^\circ \Rightarrow a+b=x\]
Therefore,\[~\Delta ACD=\Delta A+\Delta B\]
Proof: In \[\Delta ABC,a+b+c=180{}^\circ \]
but,\[c+x=180{}^\circ \] (Linear pair) \[c={{180}^{0}}-x\]
Putting "c" in the above equation, we get
\[a+b+180{}^\circ -x=180{}^\circ \Rightarrow a+b=x\]
Therefore,\[~\Delta ACD=\Delta A+\Delta B\]
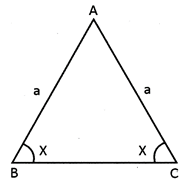
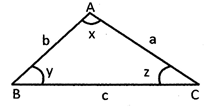 In the above given triangle all the sides of triangle denoted by a, b and c are unequal and angles x, y and z are also unequal.
In the above given triangle all the sides of triangle denoted by a, b and c are unequal and angles x, y and z are also unequal.




