Rational Numbers
- Natural numbers (N): 1, 2, 3, 4 ... etc., are called natural numbers.
- Whole numbers (W): 0, 1, 2, 3...... etc., are called whole numbers.
- Integers (Z): ....... -3, -2, -1, 0, 1, 2, 3 …… etc., are called integers, denoted by I or Z.
1, 2, 3, 4, etc., are called positive integers denoted by 7. \[{{Z}^{+}}\].
-1, -2, - 3, - 4,...... etc., are called negative integers denoted by Z-
Note: 0 is neither positive nor negative.
The numbers of the form \[\frac{x}{y}\], where x and y are natural numbers, are known as fractions.
e.g.\[\frac{3}{5},\frac{2}{1},\frac{1}{125},\]......... etc.
A number of the form \[\frac{p}{q}\](q\[\ne \]O), where p and q are integers is called a rational number.
e.g.,\[\frac{-3}{17},\frac{5}{-19},\frac{10}{1},\frac{-11}{-23},\]…. etc.
Note: 0 is a rational number, since 0=\[\frac{\mathbf{0}}{\mathbf{1}}\].
- A rational number r- is positive if p and q are either both positive and both negative.
e.g., \[\frac{3}{5},\frac{-2}{-7}\]
- A rational number \[\frac{p}{q}\]is negative if either of p and q is positive and the other is negative.
e.g., \[\frac{-5}{3},\frac{7}{-23}\]
Note: 0 is neither a positive nor a negative rational number.
- Representation of Rational numbers on a number line:
We can mark rational numbers on a number line just as we do integers.
The negative rational numbers are marked to the left of 0 and the positive rational numbers are marked to the right of 0.
Thus,,\[\frac{1}{3}and-\frac{1}{3}\]would be at an equal distance from 0 but on its either side.
Similarly, other rational numbers with different denominators can also be represented on the number line.
Thus, in general, any rational number is either of the following two types.
(i)\[\frac{m}{n}\] where m < n (ii)\[\frac{m}{n}\] where m > n
e.g., 4, 6 \[\frac{1}{2},\frac{3}{4},\frac{5}{6}\]etc.,
e.g.,\[\frac{7}{6},\frac{3}{2},\frac{15}{6}\] etc.
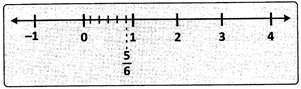
Representation of\[\frac{\mathbf{m}}{\mathbf{n}}\] on the number line where m < n:
The rational number - (5 < 6) is represented on the number line as shown.
- Representation of \[\frac{\mathbf{m}}{\mathbf{n}}\]on the number line where m > n:
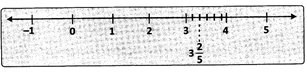
Consider the rational number \[\frac{17}{5}\].
First convert the rational number\[\frac{17}{5}\]into a mixed fraction and then mark it on the number line i.e. 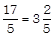
- Standard form of a rational number:
A rational number'\[\frac{p}{q}\]is
more...
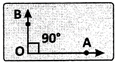 (ii) Acute angle: An angle whose measure is less than 90° is called an acute angle.
(ii) Acute angle: An angle whose measure is less than 90° is called an acute angle.
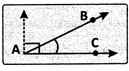 (iii) Obtuse angle: An angle whose measure is greater than 90° but less than 180° is called an obtuse angle.
more...
(iii) Obtuse angle: An angle whose measure is greater than 90° but less than 180° is called an obtuse angle.
more... 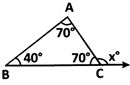 e.g., Exterior angle,
\[{{x}^{o}}=\angle A+\angle B={{70}^{o}}+{{40}^{o}}=\,{{110}^{o}}\]
e.g., Exterior angle,
\[{{x}^{o}}=\angle A+\angle B={{70}^{o}}+{{40}^{o}}=\,{{110}^{o}}\]
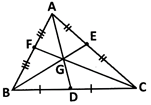 Here AD, BE and CF are medians of \[\Delta \]ABC.
Here AD, BE and CF are medians of \[\Delta \]ABC.
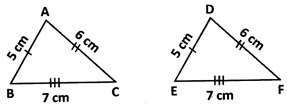 In the given figure, \[\Delta \]ABC =\[\Delta \]DEF by S.S.S. congruence condition.
In the given figure, \[\Delta \]ABC =\[\Delta \]DEF by S.S.S. congruence condition.
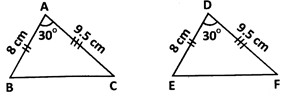 in the given figure, AABC '= ADEF by S.A.S. congruence condition.
in the given figure, AABC '= ADEF by S.A.S. congruence condition.
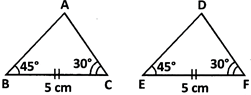
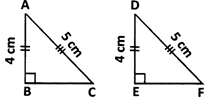 In the given figure,\[\Delta \]ABC\[\cong \]\[\Delta \]DEF by R.H.S. more...
In the given figure,\[\Delta \]ABC\[\cong \]\[\Delta \]DEF by R.H.S. more... 


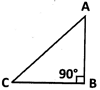 \[\operatorname{Here},A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]
\[\operatorname{Here},A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]