JEE Main & Advanced Physics Simple Harmonic Motion Super Position of S.H.M's (Lissajous Figures)

If two S.H.M's act in perpendicular directions, then their resultant motion is in the form of a straight line or a circle or a parabola etc. depending on the frequency ratio of the two S.H.M. and initial phase difference. These figures are called Lissajous figures.

Let the equations of two mutually perpendicular S.H.M's of same frequency be

\[x={{a}_{1}}\sin \omega \,t\] and \[y={{a}_{2}}\sin (\omega \,t+\varphi )\]

then the general equation of Lissajou's figure can be obtained as \[\frac{{{x}^{2}}}{a_{1}^{2}}+\frac{{{y}^{2}}}{a_{2}^{2}}-\frac{2xy}{{{a}_{1}}{{a}_{2}}}\cos \varphi ={{\sin }^{2}}\varphi \]

For \[\phi ={{0}^{o}}\]: \[\frac{{{x}^{2}}}{a_{1}^{2}}+\frac{{{y}^{2}}}{a_{2}^{2}}-\frac{2xy}{{{a}_{1}}{{a}_{2}}}=0\]\[\Rightarrow \]\[{{\left( \frac{x}{{{a}_{1}}}-\frac{y}{{{a}_{2}}} \right)}^{2}}=0\]

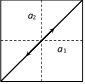
\[\Rightarrow \]\[\frac{x}{{{a}_{1}}}=\frac{y}{{{a}_{2}}}\Rightarrow y=\frac{{{a}_{2}}}{{{a}_{1}}}x\]

This is a straight line passes through origin and it's slope is \[\frac{{{a}_{2}}}{{{a}_{1}}}\].

Lissajou's figures in other conditions (with \[\frac{{{\omega }_{1}}}{{{\omega }_{2}}}=1)\]

Phase diff. \[(\phi )\]	Equation	Figure
\[\frac{\pi }{4}\]	\[\frac{{{x}^{2}}}{a_{1}^{2}}+\frac{{{y}^{2}}}{a_{2}^{2}}-\frac{\sqrt{2}xy}{{{a}_{1}}{{a}_{2}}}=\frac{1}{2}\]	Oblique ellipse
\[\frac{\pi }{2}\]	\[\frac{{{x}^{2}}}{a_{1}^{2}}+\frac{{{y}^{2}}}{a_{2}^{2}}=1\]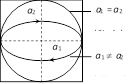
\[\frac{3\pi }{4}\]	\[\frac{{{x}^{2}}}{a_{1}^{2}}+\frac{{{y}^{2}}}{a_{2}^{2}}-\frac{\sqrt{2}xy}{{{a}_{1}}{{a}_{2}}}=\frac{1}{2}\]	Oblique ellipse
\[\pi \]	\[\frac{x}{a_{1}^{{}}}+\frac{y}{a_{2}^{{}}}=0\] \[\Rightarrow \]\[y=-\frac{{{a}_{2}}}{{{a}_{1}}}x\]	Straight line

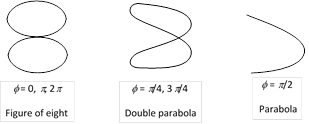
For the frequency ratio \[{{\omega }_{1}}\ :\ {{\omega }_{2}}\ =2:1\] the two perpendicular S.H.M's are

\[x={{a}_{1}}\sin (\omega t+\varphi )\] and \[y={{a}_{2}}\sin \omega t\]

Different Lissajou's figures as follows