Free, Damped, Forced and Maintained Oscillations
Category : JEE Main & Advanced

(1) Free oscillation
(i) The oscillation of a particle with fundamental frequency under the influence of restoring force are defined as free oscillations
(ii) The amplitude, frequency and energy of oscillation remains constant
(iii) Frequency of free oscillation is called natural frequency because it depends upon the nature and structure of the body.
(2) Damped oscillation
(i) The oscillation of a body whose amplitude goes on decreasing with time are defined as damped oscillation
(ii) In these oscillation the amplitude of oscillation decreases exponentially due to damping forces like frictional force, viscous force, hystersis etc.
(iii) Due to decrease in amplitude the energy of the oscillator also goes on decreasing exponentially

(iv) The force produces a resistance to the oscillation is called damping force.
If the velocity of oscillator is v then
Damping force \[{{F}_{d}}=-\,bv,\] b = damping constant
(v) Resultant force on a damped oscillator is given by
\[F={{F}_{R}}+{{F}_{d}}=-Kx-Kv\]\[\Rightarrow \frac{m{{d}^{2}}x}{d{{t}^{2}}}+b\frac{dx}{dt}+Kx=0\]
(vi) Displacement of damped oscillator is given by
\[x={{x}_{m}}{{e}^{-bt/2m}}\sin ({\omega }'t+\varphi )\] where \[{\omega }'=\]angular frequency of the damped oscillator \[=\sqrt{\omega _{0}^{2}-{{(b/2m)}^{2}}}\]
The amplitude decreases continuously with time according to
\[x={{x}_{m}}{{e}^{-(b/2m)t}}\]
(vii) For a damped oscillator if the damping is small then the mechanical energy decreases exponentially with time as
\[E=\frac{1}{2}Kx_{m}^{2}{{e}^{-bt/m}}\]
(3) Forced oscillation
(i) The oscillation in which a body oscillates under the influence of an external periodic force are known as forced oscillation
(ii) The amplitude of oscillator decrease due to damping forces but on account of the energy gained from the external source it remains constant.
(iii) Resonance : When the frequency of external force is equal to the natural frequency of the oscillator. Then this state is known as the state of resonance. And this frequency is known as resonant frequency.
(iv) While swinging in a swing if you apply a push periodically by pressing your feet against the ground, you find that not only the oscillations can now be maintained but the amplitude can also be increased. Under this condition the swing has forced or driven oscillation.
(v) In forced oscillation, frequency of damped oscillator is equal to the frequency of external force.
(vi) Suppose an external driving force is represented by
\[F(t)={{F}_{0}}\cos {{\omega }_{d}}t\]
The motion of a particle under combined action of
(a) Restoring force \[(-Kx)\]
(b) Damping force \[(-bv)\]and
(c) Driving force \[F(t)\] is given by \[ma=-Kx-bv+{{F}_{0}}\cos {{\omega }_{d}}t\]
\[\Rightarrow \]\[{{m}^{2}}\frac{{{d}^{2}}x}{{{d}^{2}}}+Kx+b\frac{dx}{dt}={{F}_{0}}\cos {{\omega }_{d}}t\]
The solution of this equation gives \[x={{x}_{0}}\sin ({{\omega }_{d}}t+\varphi )\] with amplitude \[{{x}_{0}}=\frac{{{F}_{0}}/m}{\sqrt{({{\omega }^{2}}-\omega _{0}^{2})+{{(b\omega /m)}^{2}}}}\] and \[\tan \theta =\frac{({{\omega }^{2}}-\omega _{0}^{2})}{b\omega /m}\]
where \[{{\omega }_{0}}=\sqrt{\frac{K}{m}}=\] Natural frequency of oscillator.
(vii) Amplitude resonance : The amplitude of forced oscillator depends upon the frequency \[{{\omega }_{d}}\] of external force.
When \[\omega ={{\omega }_{d}},\] the amplitude is maximum but not infinite because of presence of damping force. The corresponds frequency is called resonant frequency \[({{\omega }_{0}})\].
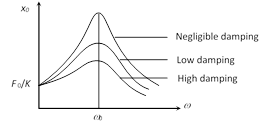
(viii) Energy resonance : At \[\omega ={{\omega }_{0}},\] oscillator absorbs maximum kinetic energy from the driving force system this state is called energy resonance.
At resonance the velocity of a driven oscillator is in phase with the driving term.
The sharpness of the resonance of a driven oscillator depends on the damping.
In the driven oscillator, the power input of the driving term in maximum at resonance.
(4) Maintained oscillation : The oscillation in which the loss of oscillator is compensated by the supplying energy from an external source are known as maintained oscillation.
You need to login to perform this action.
You will be redirected in
3 sec
