JEE Main & Advanced Physics Simple Harmonic Motion Some Important Definitions

(1) Time period (T) : It is the least interval of time after which the periodic motion of a body repeats itself. S.I. unit of time period is second.

(2) Frequency (n) : It is defined as the number of oscillations executed by body per second. S.I unit of frequency is hertz (Hz).

(3) Angular Frequency \[(\omega )\]: Angular frequency of a body executing periodic motion is equal to product of frequency of the body with factor \[2\pi \]. Angular frequency \[\omega =2\pi n\] Its unit is rad/sec.

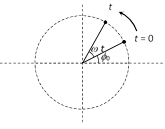
(4) Phase \[(\phi )\]: Phase of a vibrating particle at any instant is a physical quantity, which completely express the position and direction of motion, of the particle at that instant with respect to its mean position.

In oscillatory motion the phase of a vibrating particle is the argument of sine or cosine function involved to represent the generalised equation of motion of the vibrating particle.

\[y=a\sin \theta =a\sin (\omega \,t+{{\varphi }_{0}})\]

here, \[\theta =\omega \,t+{{\varphi }_{0}}\]= phase of vibrating particle.

\[{{\phi }_{0}}=\]Initial phase or epoch. It is the phase of a vibrating particle at \[t=0\].

(1) Same phase : Two vibrating particle are said to be in same phase, if the phase difference between them is an even multiple of \[\pi \] or path difference is an even multiple of \[(\lambda /2)\] or time interval is an even multiple of (T / 2) because 1 time period is equivalent to \[2\pi \] rad or 1 wave length \[(\lambda )\].

(2) Opposite phase : When the two vibrating particles cross their respective mean positions at the same time moving in opposite directions, then the phase difference between the two vibrating particles is \[{{180}^{o}}\].

Opposite phase means the phase difference between the particle is an odd multiple of \[\pi (say\,\,\pi ,\,\,3\pi ,\,\,5\pi ,\,\,7\pi .....)\] or the path difference is an odd multiple of          \[\lambda (\text{say}\,\,\frac{\lambda }{2},\,\frac{3\lambda }{2}\,,......)\] or the time interval is an odd multiple of (T / 2).

(3) Phase difference :  If two particles performs S.H.M and their equation are

\[{{y}_{1}}=a\sin (\omega \,t+{{\varphi }_{1}})\]and \[{{y}_{2}}=a\sin (\omega \,t+{{\varphi }_{2}})\] then phase difference \[\Delta \varphi =(\omega \,t+{{\varphi }_{2}})-(\omega \,t+{{\varphi }_{1}})\]\[={{\varphi }_{2}}-{{\varphi }_{1}}\]