Spring Pendulum
Category : JEE Main & Advanced
A point mass suspended from a mass less spring or placed on a frictionless horizontal plane attached with spring (fig.) constitutes a linear harmonic spring pendulum
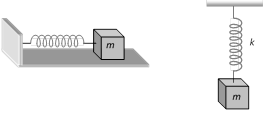
Time period \[T=2\pi \sqrt{\frac{\text{Inertia}\,\text{factor}}{\text{Spring}\,\text{factor}}}\]\[=2\pi \sqrt{\frac{m}{k}}\]
and Frequency \[n=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\]
(1) Time period of a spring pendulum depends on the mass suspended \[\Rightarrow T\propto \sqrt{m}\] or \[n\propto \frac{1}{\sqrt{m}}\]i.e. greater the mass greater will be the inertia and so lesser will be the frequency of oscillation and greater will be the time period.
(2) The time period depends on the force constant k of the spring i.e. \[T\propto \frac{1}{\sqrt{k}}\] or \[n\propto \sqrt{k}\,\,\]
(3) Time of a spring pendulum is independent of acceleration due to gravity. That is why a clock based on spring pendulum will keep proper time every where on a hill or moon or in a satellite and time period of a spring pendulum will not change inside a liquid if damping effects are neglected.
(4) Massive spring : If the spring has a mass M and mass m is suspended from it, effective mass is given by \[{{m}_{eff}}=m+\frac{M}{3}\]. Hence \[T=2\pi \sqrt{\frac{{{m}_{eff}}}{k}}\]
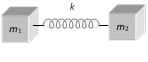
(5) Reduced mass : If two masses of mass \[{{m}_{1}}\] and \[{{m}_{2}}\] are connected by a spring and made to oscillate on horizontal surface, the reduced mass \[{{m}_{r}}\] is given by \[v=a\omega \sqrt{1-{{\sin }^{2}}\omega \,t}\] so that \[\left| \,\sin \,\omega \,t\, \right|=\text{maximum}=1\]
(6) If a spring pendulum, oscillating in a vertical plane is made to oscillate on a horizontal surface, (or on inclined plane) time period will remain unchanged.
(7) Equilibrium position for a spring in a horizontal plain is the position of natural length of spring as weight is balanced by reaction. While in case of vertical motion equilibrium position will be \[l+{{y}_{0}}\] with \[k{{y}_{0}}=mg\]
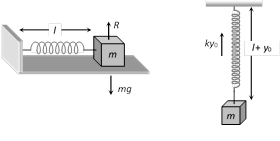
If the stretch in a vertically loaded spring is \[{{y}_{0}}\] then for equilibrium of mass m, \[k{{y}_{0}}=mg\] i.e. \[\frac{m}{k}=\frac{{{y}_{0}}}{g}\]
So that \[T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{{{y}_{0}}}{g}}\]
Time period does not depends on ?g? because along with g, \[{{y}_{o}}\] will also change in such a way that \[\frac{{{y}_{0}}}{g}=\frac{m}{k}\] remains constant
You need to login to perform this action.
You will be redirected in
3 sec
