Oscillation of Pendulum in Different Situations
Category : JEE Main & Advanced
(1) Oscillation in liquid : If bob a simple pendulum of density \[\rho \] is made to oscillate in some fluid of density \[\sigma \](where \[\sigma <\rho \]) then time period of simple pendulum gets increased.
As thrust will oppose its weight hence \[m{{g}_{eff.}}=mg-\]Thrust
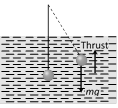
or \[{{g}_{eff.}}=g-\frac{V\sigma g}{V\rho }\] i.e \[{{g}_{eff.}}=g\,\left[ 1-\frac{\sigma }{\rho } \right]\]
\[\Rightarrow \] \[\frac{g'}{g}=\frac{\rho -\sigma }{\rho }\]
\[\Rightarrow \] \[\frac{T\,'}{T}=\sqrt{\frac{g}{g'}}=\sqrt{\frac{\rho }{\rho -\sigma }}>1\]
(2) Oscillation under the influence of electric field : If a bob of mass m carries a positive charge q and pendulum is placed in a uniform electric field of strength E
(i) If electric field directed vertically upwards.
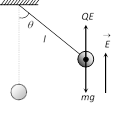
Effective acceleration
\[{{g}_{eff.}}=g-\frac{qE}{m}\]
So \[T=2\pi \sqrt{\frac{l}{g-\frac{qE}{m}}}\]
(ii) If electric field is vertically downward then
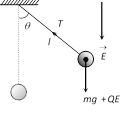
\[{{g}_{eff.}}=g+\frac{qE}{m}\] \[T=2\pi \sqrt{\frac{l}{g+\frac{qE}{m}}}\]
(3) Pendulum in a lift : If the pendulum is suspended from the ceiling of the lift.
(i) If the lift is at rest or moving down ward /up ward with constant velocity.

\[T=2\pi \sqrt{\frac{l}{g}}\]
and \[n=\frac{1}{2\pi }\sqrt{\frac{g}{l}}\]
(ii) If the lift is moving up ward with constant acceleration a

\[T=2\pi \sqrt{\frac{l}{g+a}}\] and \[n=\frac{1}{2\pi }\sqrt{\frac{g+a}{l}}\]
Time period decreases and frequency increases
(iii) If the lift is moving down ward with constant acceleration a
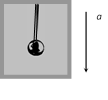
\[T=2\pi \sqrt{\frac{l}{g-a}}\] and \[n=\frac{1}{2\pi }\sqrt{\frac{g-a}{l}}\]
Time period increase and frequency decreases
(iv) If the lift is moving down ward with acceleration \[a=g\]
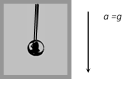
\[T=2\pi \sqrt{\frac{l}{g-g}}=\infty \]
and \[n=\frac{1}{2\pi }\sqrt{\frac{g-g}{l}}=0\]
It means there will be no oscillation in a pendulum.
Similar is the case in a satellite and at the centre of earth where effective acceleration becomes zero and pendulum will stop.
(4) Pendulum in an accelerated vehicle : The time period of simple pendulum whose point of suspension moving horizontally with acceleration a
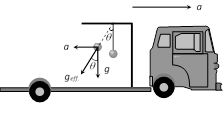
In this case effective acceleration \[{{g}_{eff.}}=\sqrt{{{g}^{2}}+{{a}^{2}}}\]
\[T=2\pi \sqrt{\frac{l}{{{({{g}^{2}}+{{a}^{2}})}^{1/2}}}}\] and \[\theta ={{\tan }^{-1}}(a/g)\,\,\]
If simple pendulum suspended in a car that is moving with constant speed v around a circle of radius r.
\[T=2\pi \frac{\sqrt{l}}{\sqrt{{{g}^{2}}+{{\left( \frac{{{v}^{2}}}{r} \right)}^{2}}}}\]
You need to login to perform this action.
You will be redirected in
3 sec
