JEE Main & Advanced Physics Simple Harmonic Motion Energy in S.H.M.

(1) Potential energy : This is an account of the displacement of the particle from its mean position.

(i) The restoring force \[F=-ky\] against which work has to be done. Hence potential energy U is given by

\[U=\int{dU}=-\int{dW}=-\int_{\,0}^{\,x}{Fdx}=\int_{\,0}^{\,y}{ky\,dy}=\frac{1}{2}k{{y}^{2}}+{{U}_{0}}\]

where \[{{U}_{0}}=\] Potential energy at equilibrium position.

If   \[{{U}_{0}}=0\] then \[U=\frac{1}{2}m{{\omega }^{2}}{{y}^{2}}\]                                                        [As\[{{\omega }^{2}}=k/m\]]

(ii) Also \[U=\frac{1}{2}m{{\omega }^{2}}{{a}^{2}}{{\sin }^{2}}\omega \,t\]\[=\frac{1}{4}m{{\omega }^{2}}{{a}^{2}}(1-\cos 2\omega \,t)\]  

[As \[y=a\sin \omega \,t\]]

Hence potential energy varies periodically with double the frequency of S.H.M.

(iii) Potential energy maximum and equal to total energy at extreme positions

\[{{U}_{\max }}=\frac{1}{2}k{{a}^{2}}=\frac{1}{2}m{{\omega }^{2}}{{a}^{2}}\] when \[y=\pm a\]; \[\omega \,t=\pi /2\]; \[t=\frac{T}{4}\]

(iv) Potential energy is minimum at mean position

\[{{U}_{\min }}=0\]         when    \[y=0\];  \[\omega \,t=0\];  \[t=0\]

(2) Kinetic energy : This is because of the velocity of the particle

Kinetic Energy  \[K=\frac{1}{2}m{{v}^{2}}\]\[=\frac{1}{2}m{{\omega }^{2}}({{a}^{2}}-{{y}^{2}})\]                                [As \[v=\omega \sqrt{{{a}^{2}}-{{y}^{2}}}\]]

(i) Also \[K=\frac{1}{2}m{{\omega }^{2}}{{a}^{2}}{{\cos }^{2}}\omega \,t\]\[=\frac{1}{4}m{{\omega }^{2}}{{a}^{2}}(1+\cos 2\omega t)\]                       

[As \[v=a\omega \,\cos \omega \,t\]]

Hence kinetic energy varies periodically with double the frequency of S.H.M.

(ii) Kinetic energy is maximum at mean position and equal to total energy at mean position.

\[{{K}_{\max }}=\frac{1}{2}m{{\omega }^{2}}{{a}^{2}}\] when \[y=0\]; \[t=0\]; \[\omega \,t=0\]

(iii) Kinetic energy is minimum at extreme position. \[{{K}_{\min }}=0\] when \[y=a\];  \[t=T/4\], \[\omega \,t=\pi /2\]

(3) Total mechanical energy : Total mechanical energy always remains constant and it is equal to sum of potential energy and kinetic energy i.e. \[E=U+K\]

\[E=\frac{1}{2}m{{\omega }^{2}}({{a}^{2}}-{{y}^{2}})+\frac{1}{2}m{{\omega }^{2}}{{y}^{2}}\]\[=\frac{1}{2}m{{\omega }^{2}}{{a}^{2}}\]

Total energy is not a position function.

(4) Energy position graph

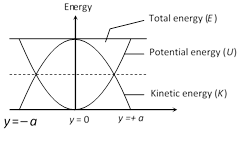
(i) At \[y=0;\,\,U=0\] and \[K=E\]

(ii) At \[y=\pm a;\,\,U=E\] and \[K=0\]

(iii) At \[y=\pm \frac{a}{2}\]; \[U=\frac{E}{4}\]and \[K=\frac{3E}{4}\]

(iv) At \[y=\pm \frac{a}{\sqrt{2}}\]; \[U=K=\frac{E}{2}\]