Velocity in S.H.M.
Category : JEE Main & Advanced
(1) Velocity of the particle executing S.H.M. at any instant, is defined as the time rate of change of its displacement at that instant.
(2) In case of S.H.M. when motion is considered from the equilibrium position, displacement \[y=a\sin \omega \,t\]
So \[v=\frac{dy}{dt}=a\omega \cos \omega \,t\]\[=a\omega \sqrt{1-{{\sin }^{2}}\omega \,t}\]\[=\omega \sqrt{{{a}^{2}}-{{y}^{2}}}\]
[As \[\sin \omega t=y/a\]]
(3) At mean position or equilibrium position \[(y=0\,\,\text{and }\,\theta =\omega t=0),\] velocity of particle is maximum and it is \[{{v}_{\max }}=a\omega \].
(4) At extreme position \[(y=\pm a\,\,\text{and}\,\,\theta =\omega t=\pi /2),\] velocity of oscillating particle is zero i.e. \[v=0\].
(5) From \[v=\omega \sqrt{{{a}^{2}}-{{y}^{2}}}\]\[\Rightarrow \] \[{{v}^{2}}={{\omega }^{2}}({{a}^{2}}-{{y}^{2}})\]\[\Rightarrow \]\[\frac{{{v}^{2}}}{{{\omega }^{2}}}={{a}^{2}}-{{y}^{2}}\]
\[\Rightarrow \] \[\frac{{{v}^{2}}}{{{a}^{2}}{{\omega }^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]
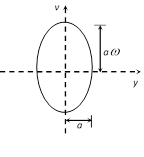
This is the equation of ellipse. Hence the graph between v and y is an ellipse.
For \[\omega =1,\] graph between v and y is a circle.
(6) Direction of velocity is either towards or away from mean position depending on the position of particle.
You need to login to perform this action.
You will be redirected in
3 sec
