Factor Affecting Time Period of Simple Pendulum
Category : JEE Main & Advanced
(1) Amplitude : The period of simple pendulum is independent of amplitude as long as its motion is simple harmonic. But if \[\theta \] is not small, \[\sin \theta \ne \theta \] then motion will not remain simple harmonic but will become oscillatory. In this situation if \[{{\theta }_{0}}\] is the amplitude of motion. Time period
\[T=2\pi \sqrt{\frac{l}{g}}\left[ 1+\frac{1}{{{2}^{2}}}{{\sin }^{2}}\left( \frac{{{\theta }_{0}}}{2} \right)+....... \right]\approx {{T}_{0}}\left[ 1+\frac{{{\theta }_{0}}^{2}}{16} \right]\]
(2) Mass of the bob : Time period of simple pendulum is also independent of mass of the bob. This is why
(i) If the solid bob is replaced by a hollow sphere of same radius but different mass, time period remains unchanged.
(ii) If a girl is swinging in a swing and another sits with her, the time period remains unchanged.
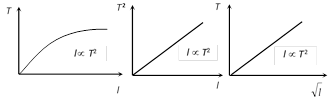
(3) Length of the pendulum : Time period \[T\propto \sqrt{l}\] where \[l\] is the distance between point of suspension and center of mass of bob and is called effective length.
(i) When a sitting girl on a swinging swing stands up, her center of mass will go up and so l and hence T will decrease.
(ii) If a hole is made at the bottom of a hollow sphere full of water and water comes out slowly through the hole and time period is recorded till the sphere is empty, initially and finally the center of mass will be at the center of the sphere. However, as water drains off the sphere, the center of mass of the system will first move down and then will come up. Due to this l and hence T first increase, reaches a maximum and then decreases till it becomes equal to its initial value.
(iii) Different graphs
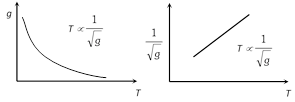
(4) Effect of g :\[T\propto \frac{1}{\sqrt{g}}\] i.e. as g increase T decreases.
(i) As we go high above the earth surface or we go deep inside the mines the value of g decrease, hence time period of pendulum (T) increases.
(ii) If a clock, based on simple pendulum is taken to hill (or on any other planet), g will decrease so T will increases and clock will become slower.
(iii) Different graphs
(5) Effect of temperature on time period : If the bob of simple pendulum is suspended by a wire then effective length of pendulum will increase with the rise of temperature due to which the time period will increase.
\[l={{l}_{0}}(1+\alpha \,\Delta \theta )\] (If \[\Delta \theta \] is the rise in temperature, \[{{l}_{0}}=\] initial length of wire, \[l=\] final length of wire)
\[\frac{T}{{{T}_{0}}}=\sqrt{\frac{l}{{{l}_{0}}}}={{(1+\alpha \,\Delta \theta )}^{1/2}}\]\[\approx 1+\frac{1}{2}\,\alpha \,\Delta \theta \]
So \[\frac{T}{{{T}_{0}}}-1=\frac{1}{2}\alpha \,\Delta \theta \] i.e. \[\frac{\Delta T}{T}\approx \frac{1}{2}\alpha \,\Delta \theta \]
You need to login to perform this action.
You will be redirected in
3 sec
