JEE Main & Advanced Physics Simple Harmonic Motion Some Other Types of Pendulum

(1) Infinite length pendulum :  If the length of the pendulum is comparable to the radius of earth then

\[T=2\pi \sqrt{\frac{1}{g\left[ \frac{1}{l}+\frac{1}{R} \right]}}\]

(i) If \[l<<R\], then \[\frac{1}{l}>>\frac{1}{R}\]  so  \[T=2\pi \sqrt{\frac{l}{g}}\]

(ii) If \[l>>R(\to \infty )\,\text{then  }\frac{1}{l}<\frac{1}{R}\]      so \[T=2\pi \sqrt{\frac{R}{g}}=2\pi \sqrt{\frac{6.4\times {{10}^{6}}}{10}}\cong 84.6\] minutes

and it is the maximum time period which an oscillating simple pendulum can have

(iii) If \[l=R\]   so  \[T=2\pi \sqrt{\frac{R}{2g}}\cong 1hour\]

(2) Second's Pendulum : It is that simple pendulum whose time period of vibrations is two seconds.

Putting \[T=2\,\sec \] and \[g=9.8m/{{\sec }^{2}}\] in \[T=2\pi \sqrt{\frac{l}{g}}\] we get \[l=\frac{4\times 9.8}{4{{\pi }^{2}}}=0.993\]\[m=99.3\,m\]

Hence length of second?s pendulum is 99.3 cm or nearly 1 meter on earth surface.

For the moon the length of the second?s pendulum will be 1/6 meter [As \[{{g}_{moon}}=\frac{{{g}_{\text{Earth}}}}{6}\]]

(3) Compound pendulum : Any rigid body suspended from a fixed support constitutes a physical pendulum. Consider the situation when the body is displaced through a small angle \[\theta \]. Torque on the body about O is given by

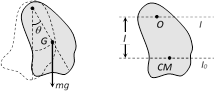
\[\tau =mgl\ \sin \theta \]                                                                                           ...(i)

where \[l=\] distance between point of suspension and centre of mass of the body.

If \[l\] be the M.I. of the body about O. Then \[\tau =I\alpha \] ...(ii)

From (i) and (ii), we get \[I\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-mgl\sin \theta \] as \[\theta \] and \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}\] are oppositely directed \[\Rightarrow \] \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-\frac{mgl}{I}\theta \] since \[\theta \]is very small

Comparing with the equation \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-{{\omega }^{2}}\theta .\]we get

\[\omega =\sqrt{\frac{mgl}{I}}

\Rightarrow T=2\pi \sqrt{\frac{I}{mgl}}\]

Also \[I={{I}_{cm}}+m{{l}^{2}}\]                (Parallel axis theorem)

\[=m{{k}^{2}}+m{{l}^{2}}\]                                          (where \[k=\] radius of gyration)

\[\therefore \] \[T=2\pi \sqrt{\frac{m{{K}^{2}}+m{{l}^{2}}}{mgl}}=2\pi \sqrt{\frac{\frac{{{K}^{2}}}{l}+l}{g}}\]\[=2\pi \sqrt{\frac{{{l}_{\text{eff}}}}{g}}\]

\[{{l}_{eff}}=\]  Effective length of pendulum = Distance between point of suspension and centre of mass.

Some common physical pendulum