NEET Physics Two Dimensional Motion Work Done by Centripetal Force

Work Done by Centripetal Force The work done by centripetal force is always zero as it is perpendicular to velocity and hence instantaneous displacement. Work done = Increment in kinetic energy of revolving body Work done = 0 Also \[W=\overrightarrow{F}\,.\,\overrightarrow{S}\,\,=\,\,F\times S\text{ }cos\,\theta \] \[=\,\, F\,\,\times \,\,S cos 9{{0}^{o}}= 0\] 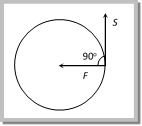Example: (i) When an electron revolve around the nucleus in hydrogen atom in a particular orbit, it neither absorb nor emit any energy means its energy remains constant. (ii) When a satellite established once in a orbit around the earth and it starts revolving with particular speed, then no fuel is required for its circular motion. Sample problem based on work done Problem 121. A particle does uniform circular motion in a horizontal plane. The radius of the circle is 20 cm. The centripetal force acting on the particle is 10 N. It?s kinetic energy is (a) 0.1 Joule       (b) 0.2 Joule       (c) 2.0 Joule       (d) 1.0 Joule Solution: (d) \[\frac{m\,{{v}^{2}}}{r}=10\,N\] (given)   Þ \[m\,{{v}^{2}}=10\times r\] \[=10\times 0.2=2\] Kinetic energy \[\frac{1}{2}m\,{{v}^{2}}=\frac{1}{2}(2)=1\,Joule.\] Problem 122. A body of mass 100 g is rotating in a circular path of radius r with constant velocity. The work done in one complete revolution is [AFMC 1998] (a) 100 r Joule    (b) (r/100) Joule (c) (100/r) Joule              (d) Zero Solution: (d) Because in uniform circular motion work done by the centripetal force is always zero. Problem 123. A particle of mass m is describing a circular path of radius r with uniform speed. If L is the angular momentum of the particle about the axis of the circle, the kinetic energy of the particle is given by [CPMT 1995] (a) \[{{L}^{2}}/m{{r}^{2}}\]  (b) \[{{L}^{2}}/2m{{r}^{2}}\]            (c) \[2{{L}^{2}}/m{{r}^{2}}\]            (d) \[m{{r}^{2}}L\] Solution: (b) Rotational kinetic energy \[E=\frac{{{L}^{2}}}{2I}\]\[=\frac{{{L}^{2}}}{2m\,{{r}^{2}}}\] (As for a particle \[I=m\,{{r}^{2}}\])  Skidding of Vehicle on a Level Road. When a vehicle turns on a circular path it requires centripetal force. If friction provides this centripetal force then vehicle can move in circular path safely if \[\operatorname{Friction} force\ge Required centripetal force\] \[\mu \,mg\ge \frac{m{{v}^{2}}}{r}\]    \[\therefore \,\,\,\,\,\,\,\,\,{{v}_{safe}}\le \sqrt{\mu rg}\] 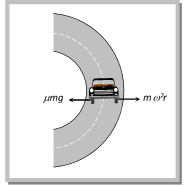This is the maximum speed by which vehicle can turn in a circular path of radius r, where coefficient of friction between the road and tyre is m. Sample problem based on skidding of vehicle on a level road Problem 124.   Find the maximum velocity for overturn for a car moved on a circular track of radius \[100m\]. The coefficient of friction between the road and tyre is \[0.2\] [CPMT 1996] (a) \[0.14\ m/s\]  (b) \[140\ m/s\]   (c) \[1.4\ km/s\]   (d) \[14\ m/s\] Solution: (d) \[{{v}_{\max }}=\sqrt{\mu \,r\,g}\]\[=\sqrt{0.2\times 100\times 10}\]\[=10\sqrt{2}\]\[=14\,m/s\] Problem 125. When the road is dry and the coefficient of friction is \[\mu \], the maximum speed of a car in a circular path is \[10\ m/s\]. If the road becomes wet and \[{\mu }'=\frac{\mu }{2}\], what is the maximum speed permitted (a) \[5\ m/s\]       (b) \[10\ m/s\]     (c) \[10\sqrt{2}\ m/s\]      (d) \[5\sqrt{2}\ m/s\] Solution : (d) \[v\propto \sqrt{\mu }\Rightarrow \frac{{{v}_{2}}}{{{v}_{1}}}=\sqrt{\frac{{{\mu }_{2}}}{{{\mu }_{1}}}}=\sqrt{\frac{\mu /2}{\mu }}=\frac{1}{\sqrt{2}}\Rightarrow {{v}_{2}}=\frac{1}{\sqrt{2}}{{v}_{1}}\Rightarrow {{v}_{2}}=\frac{10}{\sqrt{2}}=5\sqrt{2}\,m/s\] Problem 126. The coefficient of friction between the tyres and the road is 0.25. The maximum speed with which a car can be driven round a curve of radius 40 m with skidding is (assume g = 10 ms?2) [Kerala PMT 2002] (a) \[40\,m{{s}^{-1}}\] (b) \[20\,m{{s}^{-1}}\] (c) \[15\,m{{s}^{-1}}\]  (d) \[10\,m{{s}^{-1}}\] Solution: (d) \[{{v}_{\max }}=\sqrt{\mu \,r\,g}\]\[=\sqrt{0.25\times 40\times 10}\]\[=10\,m/s\]  Skidding of Object on a Rotating Platform. On a rotating platform, to avoid the skidding of an object (mass m) placed at a distance r from axis of rotation, the centripetal force should be provided by force of friction. Centripetal force = Force of friction                   mw2r = mmg             \[\therefore \,\,\,\,\,\,\,\,\,\,{{\omega }_{\max }}=\sqrt{(\mu g/r)}\,,\] Hence maximum angular velocity of rotation of the platform is \[\sqrt{(\mu g/r)}\,,\] so that object will not skid on it.  Bending of a Cyclist. A cyclist provides himself the necessary centripetal force by leaning inward on a horizontal track, while going round a curve. Consider a cyclist of weight mg taking a turn of radius r with velocity v. In order to provide the necessary centripetal force, the cyclist leans through angle  q inwards as shown in figure. The cyclist is under the action of the following forces: The weight mg acting vertically downward at the centre of gravity of cycle and the cyclist. The reaction R of the ground on cyclist. It will act along a line-making angle q with the vertical. The vertical component R cosq of the normal reaction R will balance the weight of the cyclist, while the horizontal component R sin q will provide the necessary centripetal force to the cyclist. \[R\sin \theta =\frac{m{{v}^{2}}}{r}\]                                      ?.. (i)               and                   R cos q  = mg                ?..(ii) 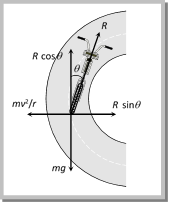Dividing equation (i) by (ii), we have \[\frac{R\sin \theta }{R\cos \theta }=\frac{m{{{v}^{2}}}/{r}\;}{mg}\]     or \[\tan \theta =\frac{{{v}^{2}}}{rg}\]             ?..? (iii) Therefore, the cyclist should bend through an angle \[\theta ={{\tan }^{-1}}\left( \frac{{{v}^{2}}}{rg} \right)\] It follows that the angle through which cyclist should bend will be greater, if (i) The radius of the curve is small i.e. the curve is sharper (ii) The velocity of the cyclist is large. Note:  q For the same reasons, an ice skater or an aeroplane has to bend inwards, while taking a turn. Sample problem based on bending of cyclist Problem 127.   A boy on a cycle pedals around a circle of 20 metres radius at a speed of 20 metres/sec. The combined mass of the boy and the cycle is \[90kg\]. The angle that the cycle makes with the vertical so that it may not fall is \[(g=9.8\ m/{{\sec }^{2}})\] [MP PMT 1995] (a) \[{{60.25}^{o}}\]    (b) \[{{63.90}^{o}}\]    (c) \[{{26.12}^{o}}\]    (d) \[{{30.00}^{o}}\] Solution: (b) \[r=20\,m,\]  \[v=20\,m/s,\]  \[m=90\,kg,\,\,\,g=9.8\,m/{{s}^{2}}\]  (given) \[\theta ={{\tan }^{-1}}\left( \frac{{{v}^{2}}}{r\,g} \right)={{\tan }^{-1}}\left( \frac{20\times 20}{20\times 10} \right)={{\tan }^{-1}}(2)\] \[=63.90{}^\circ \] Problem 128. If a cyclist moving with a speed of \[4.9\ m/s\] on a level road can take a sharp circular turn of radius \[4m\], then coefficient of friction between the cycle tyres and road is [AIIMS 1999] (a) 0.41             (b) 0.51             (c) 0.71             (d) 0.61 Solution: (d) \[v=4.9\,m/s,\]\[r=4\,m\] and \[g=9.8\,m/{{s}^{2}}\]  (given) \[\mu =\frac{{{v}^{2}}}{r\,g}=\frac{4.9\times 4.9}{4\times 9.8}\]\[=0.61\] Problem 129. A cyclist taking turn bends inwards while a car passenger taking same turn is thrown outwards. The reason is [NCERT 1972] (a) Car is heavier than cycle (b) Car has four wheels while cycle has only two (c) Difference in the speed of the two (d) Cyclist has to counteract the centrifugal force while in the case of car only the passenger is thrown by this force Solution: (d)              Banking of a Road. For getting a centripetal force cyclist bend towards the centre of circular path but it is not possible in case of four wheelers. Therefore, outer bed of the road is raised so that a vehicle moving on it gets automatically inclined towards the centre. In the figure (A) shown reaction R is resolved into two components, the component R cosq balances weight of vehicle \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,R\,\,\cos \,\,\theta =mg\]                      ?? (i) and the horizontal component R sin q  provides necessary centripetal force as it is directed towards centre of desired circle Thus \[R\,\,\sin \,\,\theta =\frac{m{{v}^{2}}}{r}\]  ...? (ii)  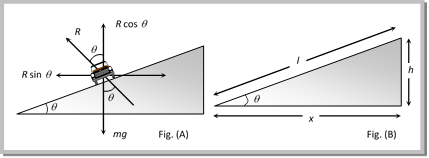                       Dividing (ii) by (i), we have                         \[\tan \,\theta =\frac{{{v}^{2}}}{r\,g}\]               ...... (iii) or         \[\tan \theta =\frac{{{\omega }^{2}}r}{g}=\frac{v\omega }{rg}\]             ...... (iv)           \[[As v = r\omega ]\] If l = width of the road, h = height of the outer edge from the ground level then from the figure (B) \[\tan \theta =\frac{h}{x}=\frac{h}{l}\]    ....... (v)           [since q  is very small] From equation (iii), (iv) and (v)      \[\tan \theta =\frac{{{v}^{2}}}{rg}\]\[=\frac{{{\omega }^{2}}r}{g}=\frac{v\omega }{rg}=\frac{h}{l}\] Note: q If friction is also present between the tyres and road then \[\frac{{{v}^{2}}}{rg}=\frac{\mu +\tan \theta }{1-\mu \tan \theta }\] q Maximum safe speed on a banked frictional road \[v=\sqrt{\frac{rg(\mu +\tan \theta )}{1-\mu \tan \theta }}\] Sample problems based on banking of a road Problem 130. For traffic moving at \[60\ km/hr\] along a circular track of radius \[0.1\ km\], the correct angle of banking is [MNR 1993] (a) \[\frac{{{(60)}^{2}}}{0.1}\] (b) \[{{\tan }^{-1}}\left[ \frac{{{(50/3)}^{2}}}{100\times 9.8} \right]\]    (c) \[{{\tan }^{-1}}\left[ \frac{100\times 9.8}{{{(50/3)}^{2}}} \right]\]         (d) \[{{\tan }^{-1}}\sqrt{60\times 0.1\times 9.8}\] Solution: (b) \[v=60\,km/hr\,=\frac{50}{3}\,m/s\],  \[r=0.1km=100\,m,\]   \[g=9.8\,m/{{s}^{2}}\]  (given) Angle of banking \[\tan \theta =\frac{{{v}^{2}}}{r\,g}\]or\[\theta ={{\tan }^{-1}}\left( \frac{{{v}^{2}}}{r\,g} \right)\] \[={{\tan }^{-1}}\left[ \frac{{{\left( 50/3 \right)}^{2}}}{100\times 9.8} \right]\] Problem 131. A vehicle is moving with a velocity \[v\] on a curved road of width \[b\] and radius of curvature \[R\]. For counteracting the centrifugal force on the vehicle, the difference in elevation required in between the outer and inner edges of the road is [EAMCET 1983; MP PMT 1996] (a) \[\frac{{{v}^{2}}b}{Rg}\]                (b) \[\frac{rb}{Rg}\]                    (c) \[\frac{v{{b}^{2}}}{Rg}\]                (d) \[\frac{vb}{{{R}^{2}}g}\] Solution: (a) For Banking of road \[\tan \theta =\frac{{{v}^{2}}}{r\,g}\]and \[\tan \theta =\frac{h}{l}\] \[\therefore \,\,\,\,\,\,\frac{{{v}^{2}}}{r\,g}=\frac{h}{l}\Rightarrow h=\frac{{{v}^{2}}l}{r\,g}=\frac{{{v}^{2}}b}{R\,g}\]             [As \[l=b\]and \[r=R\] given] Problem 132. The radius of curvature of a road at a certain turn is \[50m\]. The width of the road is \[10m\] and its outer edge is \[1.5m\] higher than the inner edge. The safe speed for such an inclination will be (a) \[6.5\ m/s\]    (b) \[8.6\ m/s\]    (c) \[8\ m/s\]       (d) \[10\ m/s\] Solution: (b) \[h=1.5\,m,\,\,\,r=50\,m,\,\,\,l=10\,m,\,\,\,g=10\,m/{{s}^{2}}\] (given) \[\frac{{{v}^{2}}}{r\,g}=\frac{h}{l}\Rightarrow v=\sqrt{\frac{hrg}{l}}=\sqrt{\frac{1.5\times 50\times 10}{10}}=8.6\,m/s\] Problem 133. Keeping the banking angle same to increase the maximum speed with which a car can travel on a curved road by 10%, the radius of curvature of road has to be changed from \[20m\] to [EAMCET 1991] (a) \[16\,m\]       (b) \[18\,m\]       (c) \[24.25\,m\]   (d) \[30.5\ m\] Solution: (c) \[\tan \theta =\frac{{{v}^{2}}}{r\,g}\Rightarrow r\propto {{v}^{2}}\] (if \[\theta \] is constant) \[\frac{{{r}_{2}}}{{{r}_{1}}}={{\left( \frac{{{v}_{2}}}{{{v}_{1}}} \right)}^{2}}={{\left( \frac{1.1v}{v} \right)}^{2}}= 1.21~\Rightarrow {{r}_{2}}=\text{ }1.21\times {{r}_{1}}=\text{ }1.21\times 20\text{ }=\text{ }24.2\,m\] Problem 134. The slope of the smooth banked horizontal road is \[p\]. If the radius of the curve be \[r\], the maximum velocity with which a car can negotiate the curve is given by (a) \[prg\]                       (b) \[\sqrt{prg}\]  (c) \[p/rg\]          (d) \[\sqrt{p/rg}\] Solution: (b) \[\tan \theta =\frac{{{v}^{2}}}{r\,g}\]\[\Rightarrow p=\frac{{{v}^{2}}}{r\,g}\]  \ \[v=\sqrt{p\,r\,g}\]  Overturning of Vehicle. When a car moves in a circular path with speed more than maximum speed then it overturns and it?s inner wheel leaves the ground first 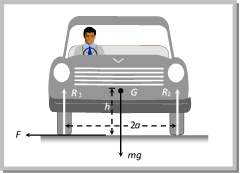Weight of the car = mg Speed of the car = v Radius of the circular path = r Distance between the centre of wheels of the car = 2a Height of the centre of gravity (G) of the car from the road level = h Reaction on the inner wheel of the car by the ground = R1 Reaction on the outer wheel of the car by the ground = R2 When a car move in a circular path, horizontal force F provides the required centripetal force i.e., \[F=\frac{m{{v}^{2}}}{R}\]                                                          ....... (i) For rotational equilibrium, by taking the moment of forces R1, R2 and F about G \[Fh+{{R}_{1}}a={{R}_{2}}a\]                                                ....... (ii) As there is no vertical motion so R1 + R2 = mg                   ....... (iii) By solving (i), (ii) and (iii) \[{{R}_{1}}=\frac{1}{2}M\left[ g-\frac{{{v}^{2}}h}{ra} \right]\]            ....... (iv) and \[{{R}_{2}}=\frac{1}{2}M\left[ g+\frac{{{v}^{2}}h}{ra} \right]\]    .......(v) It is clear from equation (iv) that if v increases value of R1 decreases and for R1 = 0 \[\frac{{{v}^{2}}h}{ra}=g\]     or         \[v=\sqrt{\frac{gra}{h}}\] i.e. the maximum speed of a car without overturning on a flat road is given by \[v=\sqrt{\frac{gra}{h}}\] Sample problems based on overturning of vehicle Problem 135. The distance between two rails is \[1.5m\]. The centre of gravity of the train at a height of \[2m\] from the ground. The maximum speed of the train on a circular path of radius \[120m\] can be (a) \[10.5\ m/s\]  (b) \[42\ m/s\]     (c) \[21\ m/s\]    (d) \[84\ m/s\] Solution: (c) Height of centre of gravity from the ground h = 2m, Acceleration due to gravity g = 10\[m/{{s}^{2}}\], Distance between two rails 2a = 1.5m, Radius of circular path r = 120 m  (given) \[{{v}_{\max }}=\sqrt{\frac{g\,r\,a}{h}}\Rightarrow {{v}_{\max }}=\sqrt{\frac{10\times 120\times 0.75}{2}}=21.2\,m/s\] Problem 136. A car sometimes overturns while taking a turn. When it overturns, it is [AFMC 1988] (a) The inner wheel which leaves the ground first (b) The outer wheel which leaves the ground first (c) Both the wheels leave the ground simultaneously (d) Either wheel leaves the ground first Solution: (a)             Problem 137. A car is moving on a circular path and takes a turn. If \[{{R}_{1}}\] and \[{{R}_{2}}\] be the reactions on the inner and outer wheels respectively, then (a) \[{{R}_{1}}={{R}_{2}}\]     (b) \[{{R}_{1}}<\ {{R}_{2}}\]   (c) \[{{R}_{1}}>\ {{R}_{2}}\]   (d) \[{{R}_{1}}\ \ge \ {{R}_{2}}\] Solution: (b) Reaction on inner wheel \[{{R}_{1}}=\frac{M}{2}\left[ g-\frac{{{v}^{2}}h}{r\,a} \right]\] and Reaction on outer wheel \[{{R}_{2}}=\frac{M}{2}\left[ g+\frac{{{v}^{2}}h}{r\,a} \right]\] \[\therefore \,\,\,\,\,{{R}_{1}}<{{R}_{2}}\] Problem 138. A train \[A\] runs from east to west and another train \[B\] of the same mass runs from west to east at the same speed along the equator. A presses the track with a force \[{{F}_{1}}\] and \[B\] presses the track with a force \[{{F}_{2}}\] (a) \[{{F}_{1}}\ >\ {{F}_{2}}\] (b) \[{{F}_{1}}<\ {{F}_{2}}\] (c) \[{{F}_{1}}={{F}_{2}}\] (d) The information is insufficient to find the relation between \[{{F}_{1}}\] and \[{{F}_{2}}\] Solution: (a) We know that earth revolves about its own axis from west to east. Let its angular speed is \[{{\omega }_{e}}\] and the angular speed of the train is \[{{\omega }_{t}}\] For train A: Net angular speed = (\[{{\omega }_{e}}-{{\omega }_{t}}\]) because the sense of rotation of train is opposite to that of earth So reaction of track \[{{R}_{1}}={{F}_{1}}=m\,g-m\,{{({{\omega }_{e}}-{{\omega }_{t}})}^{2}}R\] For train B: Net angular speed = \[({{\omega }_{e}}+{{\omega }_{t}})\] because the sense of rotation of train is same as that of earth So reaction of track \[{{R}_{2}}={{F}_{2}}=m\,g-m\,{{({{\omega }_{e}}+{{\omega }_{t}})}^{2}}R\]   So it is clear that \[{{F}_{1}}>{{F}_{2}}\]  Motion of Charged Particle in Magnetic Field. When a charged particle having mass m, charge q enters perpendicularly in a magnetic field B, with velocity v then it describes a circular path of radius r. Because magnetic force (qvB) works in the perpendicular direction of v and it provides required centripetal force Magnetic force = Centripetal force  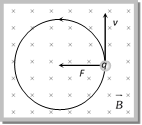 \[qvB=\frac{m{{v}^{2}}}{r}\] \[\therefore \] radius of the circular path \[r=\frac{mv}{qB}\]  Reaction of Road on Car. (1) When car moves on a concave bridge then Centripetal force \[=R-mg\cos \theta =\frac{m{{v}^{2}}}{r}\] and reaction  \[R=mg\cos \theta +\frac{m{{v}^{2}}}{r}\] 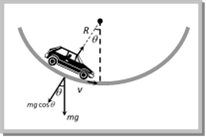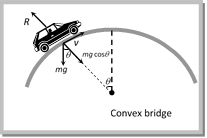(2) When car moves on a convex bridge Centripetal force = \[mg\cos \theta -R\] \[=\frac{m{{v}^{2}}}{r}\] and reaction \[R=mg\cos \theta -\frac{m{{v}^{2}}}{r}\] Sample problem based on reaction of road Problem 139. The road way bridge over a canal is in the form of an arc of a circle of radius \[20m\]. What is the minimum speed with which a car can cross the bridge without leaving contact with the ground at the highest point \[(g=9.8\ m/{{s}^{2}})\] (a) \[7\ m/s\]       (b) \[14\ m/s\]     (c) \[289\ m/s\]   (d) \[5\ m/s\] Solution: (b) At the highest point of the bridge for critical condition \[mg-\frac{m\,{{v}^{2}}}{r}=0\Rightarrow \frac{m\,{{v}^{2}}}{r}=m\,g\] \[\therefore \,\,\,{{v}_{\max }}=\sqrt{gr}=\sqrt{9.8\times 20}=\sqrt{196}=14\,m/s\] Problem 140. A car moves at a constant speed on a road as shown in the figure. The normal force exerted by the road on the car is \[{{N}_{A}}\,\,and\,\,{{N}_{B}}\] when it is at the points \[A\] and \[B\] respectively (a) \[{{N}_{A}}={{N}_{B}}\] (b) \[{{N}_{A}}>\ {{N}_{B}}\] (c) \[{{N}_{A}}<\ {{N}_{B}}\] (d) All possibilities are there Solution: (c) From the formula \[N=mg-\frac{m{{v}^{2}}}{r}\,\,\,\,\,\,\therefore \,\,\,\,N\propto r\] As \[{{r}_{A}}<\text{ }{{r}_{B}}\,\,\,\,\,\,\,\,\,\therefore \,\,\,{{N}_{A}}<{{N}_{B}}\] Problem 141. A car while travelling at a speed of \[72\ km/hr\]. Passes through a curved portion of road in the form of an arc of a radius \[10m\]. If the mass of the car is \[500\,kg\] the reaction of the car at the lowest point P is 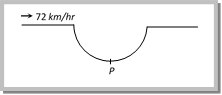(a) \[25\ kN\]                (b) \[50\ kN\]      (c) \[75\ kN\]                  (d) None of these Solution: (a) \[v=72\frac{km}{h}\,=20\,m/s,\]  \[r=10\,m,\]   \[m=500\,kg\] (given) Reaction at lowest point \[R=mg+\frac{m\,{{v}^{2}}}{r}\] \[=500\times 10+\frac{500\times {{(20)}^{2}}}{10}=25000\,\,N=25\,\,KN\]