Non Uniform Circular Motion
Category : NEET
Non Uniform Circular Motion If the speed of the particle in a horizontal circular motion changes with respect to time, then its motion is said to be non-uniform circular motion. Consider a particle describing a circular path of radius r with centre at O. Let at an instant the particle be at P and \[\overrightarrow{\upsilon }\] be its linear velocity and \[\overrightarrow{\omega }\] be its angular velocity. Then, \[\vec{\upsilon }=\vec{\omega }\times \vec{r}\] ?.. (i) Differentiating both sides of w.r.t. time t we have 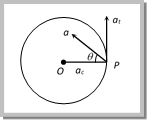 \[\frac{\overset{\to }{\mathop{d\upsilon }}\,}{dt}=\frac{\overset{\to }{\mathop{d\omega }}\,}{dt}\,\times \vec{r}\,+\,\vec{\omega }\,\times \,\frac{\overset{\to }{\mathop{dr}}\,}{dt}\] ?.. (ii) Here, \[\frac{\overset{\to }{\mathop{dv}}\,}{dt}=\vec{a},\,\,\] (Resultant acceleration) \[\vec{a}=\vec{\alpha }\,\times \,\vec{r}\,\,\,\,\,+\,\,\,\,\vec{\omega }\,\times \,\vec{\upsilon }\] \[\frac{\overset{\to }{\mathop{d\omega }}\,}{dt}=\vec{\alpha }\,\,\] (Angular acceleration) \[\vec{a}=\,\,\,\,\,\,\,{{\vec{a}}_{t}}\,\,\,\,\,+\,\,\,\,\,{{\vec{a}}_{c}}\] .?. (iii) \[\frac{\overset{\to }{\mathop{dr}}\,}{dt}=\vec{\upsilon }\,\] (Linear velocity) Thus the resultant acceleration of the particle at P has two component accelerations (1) Tangential acceleration: \[\overrightarrow{{{a}_{t}}}=\overrightarrow{\alpha }\times \overrightarrow{\,r}\] It acts along the tangent to the circular path at P in the plane of circular path. According to right hand rule since \[\vec{\alpha }\] and \[\vec{r}\] are perpendicular to each other, therefore, the magnitude of tangential acceleration is given by \[|{{\overrightarrow{a}}_{t}}|\,=\,|\overrightarrow{\alpha }\,\times \,\overrightarrow{r}|\,=\,\alpha \,r\,\sin \,{{90}^{o}}\,=\alpha \,r.\] (2) Centripetal (Radial) acceleration: \[\overrightarrow{{{a}_{c}}}=\overrightarrow{\omega }\times \overrightarrow{v}\] It is also called centripetal acceleration of the particle at P. It acts along the radius of the particle at P. According to right hand rule since \[\overrightarrow{\omega }\] and \[\overrightarrow{\upsilon }\] are perpendicular to each other, therefore, the magnitude of centripetal acceleration is given by \[|{{\vec{a}}_{c}}|\,=\,|\vec{\omega }\,\times \,\vec{\upsilon }|\,=\,\omega \,\upsilon \,\sin \,{{90}^{o}}=\omega \,\upsilon \,=\,\omega (\omega \,r)\,=\,{{\omega }^{2}}r={{\upsilon }^{2}}/r\] (3) Tangential and centripetal acceleration in different motions
\[\frac{\overset{\to }{\mathop{d\upsilon }}\,}{dt}=\frac{\overset{\to }{\mathop{d\omega }}\,}{dt}\,\times \vec{r}\,+\,\vec{\omega }\,\times \,\frac{\overset{\to }{\mathop{dr}}\,}{dt}\] ?.. (ii) Here, \[\frac{\overset{\to }{\mathop{dv}}\,}{dt}=\vec{a},\,\,\] (Resultant acceleration) \[\vec{a}=\vec{\alpha }\,\times \,\vec{r}\,\,\,\,\,+\,\,\,\,\vec{\omega }\,\times \,\vec{\upsilon }\] \[\frac{\overset{\to }{\mathop{d\omega }}\,}{dt}=\vec{\alpha }\,\,\] (Angular acceleration) \[\vec{a}=\,\,\,\,\,\,\,{{\vec{a}}_{t}}\,\,\,\,\,+\,\,\,\,\,{{\vec{a}}_{c}}\] .?. (iii) \[\frac{\overset{\to }{\mathop{dr}}\,}{dt}=\vec{\upsilon }\,\] (Linear velocity) Thus the resultant acceleration of the particle at P has two component accelerations (1) Tangential acceleration: \[\overrightarrow{{{a}_{t}}}=\overrightarrow{\alpha }\times \overrightarrow{\,r}\] It acts along the tangent to the circular path at P in the plane of circular path. According to right hand rule since \[\vec{\alpha }\] and \[\vec{r}\] are perpendicular to each other, therefore, the magnitude of tangential acceleration is given by \[|{{\overrightarrow{a}}_{t}}|\,=\,|\overrightarrow{\alpha }\,\times \,\overrightarrow{r}|\,=\,\alpha \,r\,\sin \,{{90}^{o}}\,=\alpha \,r.\] (2) Centripetal (Radial) acceleration: \[\overrightarrow{{{a}_{c}}}=\overrightarrow{\omega }\times \overrightarrow{v}\] It is also called centripetal acceleration of the particle at P. It acts along the radius of the particle at P. According to right hand rule since \[\overrightarrow{\omega }\] and \[\overrightarrow{\upsilon }\] are perpendicular to each other, therefore, the magnitude of centripetal acceleration is given by \[|{{\vec{a}}_{c}}|\,=\,|\vec{\omega }\,\times \,\vec{\upsilon }|\,=\,\omega \,\upsilon \,\sin \,{{90}^{o}}=\omega \,\upsilon \,=\,\omega (\omega \,r)\,=\,{{\omega }^{2}}r={{\upsilon }^{2}}/r\] (3) Tangential and centripetal acceleration in different motions
| Centripetal acceleration | Tangential acceleration | Net acceleration | Type of motion |
| ac = 0 | at = 0 | a = 0 | Uniform translatory motion |
| ac = 0 | at ¹ 0 | a = at | Accelerated translatory motion |
| ac ¹ 0 | at = 0 | a = ac | Uniform circular motion |
| ac ¹ 0 | at ¹ 0 | \[a=\sqrt{a_{c}^{2}+a_{t}^{2}}\] | Non-uniform circular motion |
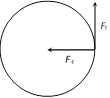 Tangential acceleration \[{{a}_{t}}=\frac{dv}{dt}=\frac{dv}{ds}\,.\,\frac{ds}{dt}\,\,\,\Rightarrow \,\,\,{{a}_{t}}=\frac{d}{ds}\left[ s\sqrt{\frac{2a}{m}} \right]\,.v\] \[{{a}_{t}}=v\sqrt{\frac{2a}{m}}=s\sqrt{\frac{2a}{m}}\,\sqrt{\frac{2a}{m}}=\frac{2as}{m}\] and \[{{F}_{t}}=m{{a}_{t}}=2as\] ?. (iii) Now substituting value of \[{{\operatorname{F}}_{c}}\,\,and {{F}_{t}}\] in equation (i) \[\therefore {{F}_{Net}}=\sqrt{{{\left( \frac{2a{{s}^{2}}}{R} \right)}^{2}}+{{\left( 2as \right)}^{2}}}=2as\,{{\left[ 1+\frac{{{s}^{2}}}{{{R}^{2}}} \right]}^{1/2}}\] Problem 143. A particle of mass \[m\] is moving in a circular path of constant radius \[r\] such that its centripetal acceleration \[{{a}_{c}}\] is varying with time \[t\] as \[{{a}_{c}}={{k}^{2}}r{{t}^{2}}\], where \[k\] is a constant. The power delivered to the particle by the forces acting on it is [IIT-JEE 1994] (a) \[2\pi m{{k}^{2}}{{r}^{2}}t\] (b) \[m{{k}^{2}}{{r}^{2}}t\] (c) \[\frac{m{{k}^{4}}{{r}^{2}}{{t}^{5}}}{3}\] (d) Zero Solution: (b) \[{{a}_{c}}={{k}^{2}}r\,{{t}^{2}}\Rightarrow \frac{{{v}^{2}}}{r}={{k}^{2}}r\,{{t}^{2}}\Rightarrow {{v}^{2}}={{k}^{2}}\,{{r}^{2}}\,{{t}^{2}}\Rightarrow \,\,v=k\,r\,t\] Tangential acceleration \[{{a}_{t}}=\frac{dv}{dt}=k\,r\] As centripetal force does not work in circular motion. So power delivered by tangential force \[P={{F}_{t}}v=m\,{{a}_{t}}v=m\left( kr \right)\text{ }krt=m{{k}^{2}}{{r}^{2}}t\] Problem 144. A simple pendulum is oscillating without damping. When the displacement of the bob is less than maximum, its acceleration vector \[\vec{a}\] is correctly shown in [IIT-JEE Screening 2002] (a)
Tangential acceleration \[{{a}_{t}}=\frac{dv}{dt}=\frac{dv}{ds}\,.\,\frac{ds}{dt}\,\,\,\Rightarrow \,\,\,{{a}_{t}}=\frac{d}{ds}\left[ s\sqrt{\frac{2a}{m}} \right]\,.v\] \[{{a}_{t}}=v\sqrt{\frac{2a}{m}}=s\sqrt{\frac{2a}{m}}\,\sqrt{\frac{2a}{m}}=\frac{2as}{m}\] and \[{{F}_{t}}=m{{a}_{t}}=2as\] ?. (iii) Now substituting value of \[{{\operatorname{F}}_{c}}\,\,and {{F}_{t}}\] in equation (i) \[\therefore {{F}_{Net}}=\sqrt{{{\left( \frac{2a{{s}^{2}}}{R} \right)}^{2}}+{{\left( 2as \right)}^{2}}}=2as\,{{\left[ 1+\frac{{{s}^{2}}}{{{R}^{2}}} \right]}^{1/2}}\] Problem 143. A particle of mass \[m\] is moving in a circular path of constant radius \[r\] such that its centripetal acceleration \[{{a}_{c}}\] is varying with time \[t\] as \[{{a}_{c}}={{k}^{2}}r{{t}^{2}}\], where \[k\] is a constant. The power delivered to the particle by the forces acting on it is [IIT-JEE 1994] (a) \[2\pi m{{k}^{2}}{{r}^{2}}t\] (b) \[m{{k}^{2}}{{r}^{2}}t\] (c) \[\frac{m{{k}^{4}}{{r}^{2}}{{t}^{5}}}{3}\] (d) Zero Solution: (b) \[{{a}_{c}}={{k}^{2}}r\,{{t}^{2}}\Rightarrow \frac{{{v}^{2}}}{r}={{k}^{2}}r\,{{t}^{2}}\Rightarrow {{v}^{2}}={{k}^{2}}\,{{r}^{2}}\,{{t}^{2}}\Rightarrow \,\,v=k\,r\,t\] Tangential acceleration \[{{a}_{t}}=\frac{dv}{dt}=k\,r\] As centripetal force does not work in circular motion. So power delivered by tangential force \[P={{F}_{t}}v=m\,{{a}_{t}}v=m\left( kr \right)\text{ }krt=m{{k}^{2}}{{r}^{2}}t\] Problem 144. A simple pendulum is oscillating without damping. When the displacement of the bob is less than maximum, its acceleration vector \[\vec{a}\] is correctly shown in [IIT-JEE Screening 2002] (a)  (b)
(b) 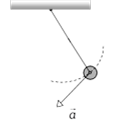 (c)
(c)  (d)
(d)  Solution: (c) \[{{a}_{c}}=\text{centripetal acceleration}\], \[{{a}_{t}}=\text{tangential acceleration}\],
Solution: (c) \[{{a}_{c}}=\text{centripetal acceleration}\], \[{{a}_{t}}=\text{tangential acceleration}\], 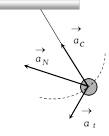 \[{{a}_{N}}=\text{ net acceleration}=\text{Resultant of}\,\,{{a}_{c}}\,\text{and}\,{{a}_{t}}\] \[{{\operatorname{a}}_{N}}=\sqrt{a_{c}^{2}+a_{t}^{2}}\] Problem 145. The speed of a particle moving in a circle of radius \[0.1\,m\] is \[v=1.0\,\,t\] where \[t\] is time in second. The resultant acceleration of the particle at \[t=5s\] will be (a) \[10\ m/{{s}^{2}}\] (b) \[100\ m/{{s}^{2}}\] (c) \[250\ m/{{s}^{2}}\] (d) \[500\ m/{{s}^{2}}\] Solution: (c) \[v=1.0\,t\Rightarrow {{a}_{t}}=\frac{dv}{dt}=1\,m/{{s}^{2}}\] and \[{{a}_{c}}=\frac{{{v}^{2}}}{r}=\frac{{{(5)}^{2}}}{0.1}=250\,m/{{s}^{2}}\] [At \[t=5\,\sec ,\,\,v=5\,m/s\]] \[\therefore \,\,\,{{a}_{N}}=\sqrt{a_{c}^{2}+a_{t}^{2}}=\sqrt{{{(250)}^{2}}+{{1}^{2}}}\Rightarrow {{a}_{N}}=250\,m/{{s}^{2}}\] (approx.) Problem 146. A particle moving along the circular path with a speed v and its speed increases by ?g? in one second. If the radius of the circular path be r, then the net acceleration of the particle is (a) \[\frac{{{v}^{2}}}{r}+g\] (b) \[\frac{{{v}^{2}}}{{{r}^{2}}}+{{g}^{2}}\] (c) \[{{\left[ \frac{{{v}^{4}}}{{{r}^{2}}}+{{g}^{2}} \right]}^{\frac{1}{2}}}\] (d) \[{{\left[ \frac{{{v}^{2}}}{r}+g \right]}^{\frac{1}{2}}}\] Solution: (c) \[{{a}_{t}}=g\] (given) and \[{{a}_{c}}=\frac{{{v}^{2}}}{r}\] and \[{{a}_{N}}=\sqrt{a_{t}^{2}+a_{c}^{2}}=\sqrt{{{\left( \frac{{{v}^{2}}}{r} \right)}^{2}}+{{g}^{2}}}=\sqrt{\frac{{{v}^{4}}}{{{r}^{2}}}+{{g}^{2}}}\] Problem 147. A car is moving with speed 30 m/sec on a circular path of radius 500 m. Its speed is increasing at the rate of \[2m/se{{c}^{2}}\]. What is the acceleration of the car [Roorkee 1982; RPET 1996; MH CET 2002; MP PMT 2003] (a) \[2 m/{{s}^{2}}\] (b) \[2.7 m/{{s}^{2}}\] (c) \[1.8 m/{{s}^{2}}\] (d) \[9.8 m/{{s}^{2}}\] Solution: (b) \[{{\operatorname{a}}_{t}}= 2\,\,m/{{s}^{2}}\] and \[{{a}_{c}}=\frac{{{v}^{2}}}{r}=\frac{30\times 30}{500}=1.8\,m/{{s}^{2}}\,\,\,\therefore \,\,a=\sqrt{a_{t}^{2}+a_{c}^{2}}=\sqrt{{{2}^{2}}+{{(1.8)}^{2}}}=2.7m/{{s}^{2}}\] Problem 148. For a particle in circular motion the centripetal acceleration is [CPMT 1998] (a) Less than its tangential acceleration (b) Equal to its tangential acceleration (c) More than its tangential acceleration (d) May be more or less than its tangential acceleration Solution: (d) Problem 149. A particle is moving along a circular path of radius 3 meter in such a way that the distance travelled measured along the circumference is given by \[S=\frac{{{t}^{2}}}{2}+\frac{{{t}^{3}}}{3}\]. The acceleration of particle when \[t=2\ \sec \] is (a) \[1.3 m/{{s}^{2}}\] (b) \[13 m/{{s}^{2}}\] (c) \[3 m/{{s}^{2}}\] (d) \[10 m/{{s}^{2}}\] Solution: (b) \[s=\frac{{{t}^{2}}}{2}+\frac{{{t}^{3}}}{3}\Rightarrow v=\frac{ds}{dt}=t+{{t}^{2}}\] and \[{{a}_{t}}=\frac{dv}{dt}=\frac{d}{dt}(t+{{t}^{2}})=1+2t\] At t = 2 sec, v = 6 m/s and \[{{a}_{t}}=5\,m/{{s}^{2}}\], \[{{a}_{c}}=\frac{{{v}^{2}}}{r}=\frac{36}{3}=12\,m/{{s}^{2}}\] \[{{a}_{N}}=\sqrt{a_{c}^{2}+a_{t}^{2}}=\sqrt{{{(12)}^{2}}+{{(5)}^{2}}}=13\,m/{{s}^{2}}\]
\[{{a}_{N}}=\text{ net acceleration}=\text{Resultant of}\,\,{{a}_{c}}\,\text{and}\,{{a}_{t}}\] \[{{\operatorname{a}}_{N}}=\sqrt{a_{c}^{2}+a_{t}^{2}}\] Problem 145. The speed of a particle moving in a circle of radius \[0.1\,m\] is \[v=1.0\,\,t\] where \[t\] is time in second. The resultant acceleration of the particle at \[t=5s\] will be (a) \[10\ m/{{s}^{2}}\] (b) \[100\ m/{{s}^{2}}\] (c) \[250\ m/{{s}^{2}}\] (d) \[500\ m/{{s}^{2}}\] Solution: (c) \[v=1.0\,t\Rightarrow {{a}_{t}}=\frac{dv}{dt}=1\,m/{{s}^{2}}\] and \[{{a}_{c}}=\frac{{{v}^{2}}}{r}=\frac{{{(5)}^{2}}}{0.1}=250\,m/{{s}^{2}}\] [At \[t=5\,\sec ,\,\,v=5\,m/s\]] \[\therefore \,\,\,{{a}_{N}}=\sqrt{a_{c}^{2}+a_{t}^{2}}=\sqrt{{{(250)}^{2}}+{{1}^{2}}}\Rightarrow {{a}_{N}}=250\,m/{{s}^{2}}\] (approx.) Problem 146. A particle moving along the circular path with a speed v and its speed increases by ?g? in one second. If the radius of the circular path be r, then the net acceleration of the particle is (a) \[\frac{{{v}^{2}}}{r}+g\] (b) \[\frac{{{v}^{2}}}{{{r}^{2}}}+{{g}^{2}}\] (c) \[{{\left[ \frac{{{v}^{4}}}{{{r}^{2}}}+{{g}^{2}} \right]}^{\frac{1}{2}}}\] (d) \[{{\left[ \frac{{{v}^{2}}}{r}+g \right]}^{\frac{1}{2}}}\] Solution: (c) \[{{a}_{t}}=g\] (given) and \[{{a}_{c}}=\frac{{{v}^{2}}}{r}\] and \[{{a}_{N}}=\sqrt{a_{t}^{2}+a_{c}^{2}}=\sqrt{{{\left( \frac{{{v}^{2}}}{r} \right)}^{2}}+{{g}^{2}}}=\sqrt{\frac{{{v}^{4}}}{{{r}^{2}}}+{{g}^{2}}}\] Problem 147. A car is moving with speed 30 m/sec on a circular path of radius 500 m. Its speed is increasing at the rate of \[2m/se{{c}^{2}}\]. What is the acceleration of the car [Roorkee 1982; RPET 1996; MH CET 2002; MP PMT 2003] (a) \[2 m/{{s}^{2}}\] (b) \[2.7 m/{{s}^{2}}\] (c) \[1.8 m/{{s}^{2}}\] (d) \[9.8 m/{{s}^{2}}\] Solution: (b) \[{{\operatorname{a}}_{t}}= 2\,\,m/{{s}^{2}}\] and \[{{a}_{c}}=\frac{{{v}^{2}}}{r}=\frac{30\times 30}{500}=1.8\,m/{{s}^{2}}\,\,\,\therefore \,\,a=\sqrt{a_{t}^{2}+a_{c}^{2}}=\sqrt{{{2}^{2}}+{{(1.8)}^{2}}}=2.7m/{{s}^{2}}\] Problem 148. For a particle in circular motion the centripetal acceleration is [CPMT 1998] (a) Less than its tangential acceleration (b) Equal to its tangential acceleration (c) More than its tangential acceleration (d) May be more or less than its tangential acceleration Solution: (d) Problem 149. A particle is moving along a circular path of radius 3 meter in such a way that the distance travelled measured along the circumference is given by \[S=\frac{{{t}^{2}}}{2}+\frac{{{t}^{3}}}{3}\]. The acceleration of particle when \[t=2\ \sec \] is (a) \[1.3 m/{{s}^{2}}\] (b) \[13 m/{{s}^{2}}\] (c) \[3 m/{{s}^{2}}\] (d) \[10 m/{{s}^{2}}\] Solution: (b) \[s=\frac{{{t}^{2}}}{2}+\frac{{{t}^{3}}}{3}\Rightarrow v=\frac{ds}{dt}=t+{{t}^{2}}\] and \[{{a}_{t}}=\frac{dv}{dt}=\frac{d}{dt}(t+{{t}^{2}})=1+2t\] At t = 2 sec, v = 6 m/s and \[{{a}_{t}}=5\,m/{{s}^{2}}\], \[{{a}_{c}}=\frac{{{v}^{2}}}{r}=\frac{36}{3}=12\,m/{{s}^{2}}\] \[{{a}_{N}}=\sqrt{a_{c}^{2}+a_{t}^{2}}=\sqrt{{{(12)}^{2}}+{{(5)}^{2}}}=13\,m/{{s}^{2}}\]
You need to login to perform this action.
You will be redirected in
3 sec
