Velocity
Category : NEET
Velocity (1) Instantaneous velocity v: In projectile motion, vertical component of velocity changes but horizontal component of velocity remains always constant. Example: When a man jumps over the hurdle leaving behind its skateboard then vertical component of his velocity is changing, but not the horizontal component, which matches with the skateboard velocity. As a result, the skateboard stays underneath him, allowing him to land on it. 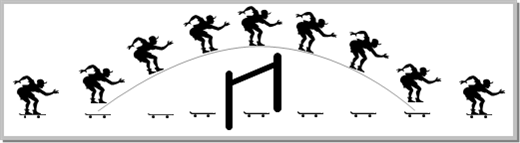 Let \[{{v}_{i}}\] be the instantaneous velocity of projectile at time t direction of this velocity is along the tangent to the trajectory at point P. \[{{\vec{v}}_{i}}={{v}_{x}}i+{{v}_{y}}\hat{j}\Rightarrow {{v}_{i}}=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{{{u}^{2}}{{\cos }^{2}}\,\theta +{{(u\sin \theta -gt)}^{2}}}\] \[{{v}_{i}}=\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}-2u\,gt\sin \theta }\] Direction of instantaneous velocity \[\tan \alpha \,=\,\frac{{{v}_{y}}}{{{v}_{x}}}=\frac{u\,\sin \,\theta -gt}{u\,\cos \theta }\] or \[\alpha ={{\tan }^{-1}}\left[ \tan \theta -\frac{gt}{u}\sec \theta \right]\] (4) Change in velocity: Initial velocity (at projection point) \[{{\overrightarrow{u}}_{i}}=u\cos \theta \,\hat{i}+u\sin \theta \,\hat{j}\] Final velocity (at highest point) \[{{\overrightarrow{u}}_{f}}=u\cos \theta \,\hat{i}+0\,\hat{j}\] (i) Change in velocity (Between projection point and highest point) \[\Delta u={{\overrightarrow{u}}_{f}}-{{\overrightarrow{u}}_{i}}=-u\sin \theta \,\hat{j}\] When body reaches the ground after completing its motion then final velocity \[{{\overrightarrow{u}}_{f}}=u\cos \theta \,\hat{i}-u\sin \theta \,\hat{j}\] (ii) Change in velocity (Between complete projectile motion) \[\Delta u={{u}_{f}}-{{u}_{i}}=-2u\sin \theta \,\hat{i}\] Sample problems based on velocity Problem 6. In a projectile motion, velocity at maximum height is [AIEEE 2002] (a) \[\frac{u\,\cos \,\theta }{2}\] (b) \[u\,\cos \,\theta \] (c) \[\frac{u\,\sin \,\theta }{2}\] (d) None of these Solution: (b) In a projectile motion at maximum height body possess only horizontal component of velocity i.e. u \[cos\,\theta \]. Problem 7. A body is thrown at angle 30o to the horizontal with the velocity of 30 m/s. After 1 sec, its velocity will be (in m/s) \[\left( g = 10 m/{{s}^{2}} \right)\] (a) \[10\sqrt{7}\] (b) \[700\sqrt{10}\] (c) \[100\sqrt{7}\] (d) \[\sqrt{40}\] Solution: (a) From the formula of instantaneous velocity \[v=\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}-2\,u\,g\,t\,\sin \theta }\] \[v=\sqrt{{{(30)}^{2}}+{{(10)}^{2}}\times {{1}^{2}}-2\times 30\times 10\times 1\times \sin {{30}^{o}}}\] \[=10\sqrt{7}\,m/s\] Problem 8. A projectile is fired at \[{{30}^{o}}\] to the horizontal. The vertical component of its velocity is 80 ms?1. Its time of flight is T. What will be the velocity of the projectile at \[\operatorname{t} = T/2\] (a) \[80\text{ }m{{s}^{1}}\] (b) \[80\sqrt{3}\,m{{s}^{-1}}\] (c) \[(80/\sqrt{3})\,m{{s}^{-1}}\] (d) \[40\text{ }m{{s}^{1}}\] Solution: (b) At half of the time of flight, the position of the projectile will be at the highest point of the parabola and at that position particle possess horizontal component of velocity only. Given \[{{u}_{vertical}}=u\sin \theta =80\Rightarrow u=\frac{80}{\sin {{30}^{o}}}=160\,m/s\] \[\therefore \,\,\,\,{{u}_{horizontal}}=u\cos \theta =160\,\,\cos {{30}^{o}}=80\sqrt{3}\,m/s.\] Problem 9. A particle is projected from point O with velocity u in a direction making an angle \[\alpha \] with the horizontal. At any instant its position is at point P at right angles to the initial direction of projection. Its velocity at point P is
Let \[{{v}_{i}}\] be the instantaneous velocity of projectile at time t direction of this velocity is along the tangent to the trajectory at point P. \[{{\vec{v}}_{i}}={{v}_{x}}i+{{v}_{y}}\hat{j}\Rightarrow {{v}_{i}}=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{{{u}^{2}}{{\cos }^{2}}\,\theta +{{(u\sin \theta -gt)}^{2}}}\] \[{{v}_{i}}=\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}-2u\,gt\sin \theta }\] Direction of instantaneous velocity \[\tan \alpha \,=\,\frac{{{v}_{y}}}{{{v}_{x}}}=\frac{u\,\sin \,\theta -gt}{u\,\cos \theta }\] or \[\alpha ={{\tan }^{-1}}\left[ \tan \theta -\frac{gt}{u}\sec \theta \right]\] (4) Change in velocity: Initial velocity (at projection point) \[{{\overrightarrow{u}}_{i}}=u\cos \theta \,\hat{i}+u\sin \theta \,\hat{j}\] Final velocity (at highest point) \[{{\overrightarrow{u}}_{f}}=u\cos \theta \,\hat{i}+0\,\hat{j}\] (i) Change in velocity (Between projection point and highest point) \[\Delta u={{\overrightarrow{u}}_{f}}-{{\overrightarrow{u}}_{i}}=-u\sin \theta \,\hat{j}\] When body reaches the ground after completing its motion then final velocity \[{{\overrightarrow{u}}_{f}}=u\cos \theta \,\hat{i}-u\sin \theta \,\hat{j}\] (ii) Change in velocity (Between complete projectile motion) \[\Delta u={{u}_{f}}-{{u}_{i}}=-2u\sin \theta \,\hat{i}\] Sample problems based on velocity Problem 6. In a projectile motion, velocity at maximum height is [AIEEE 2002] (a) \[\frac{u\,\cos \,\theta }{2}\] (b) \[u\,\cos \,\theta \] (c) \[\frac{u\,\sin \,\theta }{2}\] (d) None of these Solution: (b) In a projectile motion at maximum height body possess only horizontal component of velocity i.e. u \[cos\,\theta \]. Problem 7. A body is thrown at angle 30o to the horizontal with the velocity of 30 m/s. After 1 sec, its velocity will be (in m/s) \[\left( g = 10 m/{{s}^{2}} \right)\] (a) \[10\sqrt{7}\] (b) \[700\sqrt{10}\] (c) \[100\sqrt{7}\] (d) \[\sqrt{40}\] Solution: (a) From the formula of instantaneous velocity \[v=\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}-2\,u\,g\,t\,\sin \theta }\] \[v=\sqrt{{{(30)}^{2}}+{{(10)}^{2}}\times {{1}^{2}}-2\times 30\times 10\times 1\times \sin {{30}^{o}}}\] \[=10\sqrt{7}\,m/s\] Problem 8. A projectile is fired at \[{{30}^{o}}\] to the horizontal. The vertical component of its velocity is 80 ms?1. Its time of flight is T. What will be the velocity of the projectile at \[\operatorname{t} = T/2\] (a) \[80\text{ }m{{s}^{1}}\] (b) \[80\sqrt{3}\,m{{s}^{-1}}\] (c) \[(80/\sqrt{3})\,m{{s}^{-1}}\] (d) \[40\text{ }m{{s}^{1}}\] Solution: (b) At half of the time of flight, the position of the projectile will be at the highest point of the parabola and at that position particle possess horizontal component of velocity only. Given \[{{u}_{vertical}}=u\sin \theta =80\Rightarrow u=\frac{80}{\sin {{30}^{o}}}=160\,m/s\] \[\therefore \,\,\,\,{{u}_{horizontal}}=u\cos \theta =160\,\,\cos {{30}^{o}}=80\sqrt{3}\,m/s.\] Problem 9. A particle is projected from point O with velocity u in a direction making an angle \[\alpha \] with the horizontal. At any instant its position is at point P at right angles to the initial direction of projection. Its velocity at point P is 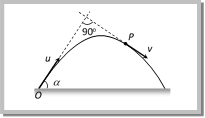 (a) \[u\text{ }tan\,\alpha \] (b) \[u\text{ }cot\,\alpha \] (c) \[u\text{ }cosec\,\alpha \] (d) \[u\text{ }sec\,\alpha \] Solution: (b) Horizontal velocity at point \['O'=u\cos \alpha \] Horizontal velocity at point \['P'=v\sin \alpha \]
(a) \[u\text{ }tan\,\alpha \] (b) \[u\text{ }cot\,\alpha \] (c) \[u\text{ }cosec\,\alpha \] (d) \[u\text{ }sec\,\alpha \] Solution: (b) Horizontal velocity at point \['O'=u\cos \alpha \] Horizontal velocity at point \['P'=v\sin \alpha \] 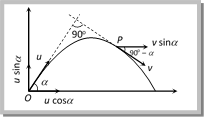 In projectile motion horizontal component of velocity remains constant throughout the motion \[\therefore \,\,\,v\sin \alpha =u\cos \alpha \Rightarrow \,v=u\cot \alpha \] Problem 10. A particle P is projected with velocity u1 at an angle of 30o with the horizontal. Another particle Q is thrown vertically upwards with velocity u2 from a point vertically below the highest point of path of P. The necessary condition for the two particles to collide at the highest point is
In projectile motion horizontal component of velocity remains constant throughout the motion \[\therefore \,\,\,v\sin \alpha =u\cos \alpha \Rightarrow \,v=u\cot \alpha \] Problem 10. A particle P is projected with velocity u1 at an angle of 30o with the horizontal. Another particle Q is thrown vertically upwards with velocity u2 from a point vertically below the highest point of path of P. The necessary condition for the two particles to collide at the highest point is  (a) \[{{u}_{1}}={{u}_{2}}\] (b) \[{{u}_{1}}=2{{u}_{2}}\] (c) \[{{u}_{1}}=\frac{{{u}_{2}}}{2}\] (d) \[{{u}_{1}}=4{{u}_{2}}\] Solution: (b) Both particle collide at the highest point it means the vertical distance travelled by both the particle will be equal, i.e. the vertical component of velocity of both particle will be equal \[{{u}_{1}}\,\sin 30{}^\circ ={{u}_{2}}\Rightarrow \frac{{{u}_{1}}}{2}={{u}_{2}}\,\,\,\,\therefore \,\,{{u}_{1}}=2{{u}_{2}}\] Problem 11. Two seconds after projection a projectile is travelling in a direction inclined at \[{{30}^{o}}\] to the horizontal after one more sec, it is travelling horizontally, the magnitude and direction of its velocity are [RPET 1999] (a) \[2\sqrt{20}\,m/\sec ,\,{{60}^{o}}\] (b) \[20\sqrt{3}\,m/\sec ,\,\,{{60}^{o}}\] (c) \[6\sqrt{40}\,\,m/\sec ,\,\,{{30}^{o}}\] (d) \[40\sqrt{6}\,m/\sec ,\,\,{{30}^{o}}\] Solution: (b) Let in 2 sec body reaches upto point A and after one more sec upto point B.
(a) \[{{u}_{1}}={{u}_{2}}\] (b) \[{{u}_{1}}=2{{u}_{2}}\] (c) \[{{u}_{1}}=\frac{{{u}_{2}}}{2}\] (d) \[{{u}_{1}}=4{{u}_{2}}\] Solution: (b) Both particle collide at the highest point it means the vertical distance travelled by both the particle will be equal, i.e. the vertical component of velocity of both particle will be equal \[{{u}_{1}}\,\sin 30{}^\circ ={{u}_{2}}\Rightarrow \frac{{{u}_{1}}}{2}={{u}_{2}}\,\,\,\,\therefore \,\,{{u}_{1}}=2{{u}_{2}}\] Problem 11. Two seconds after projection a projectile is travelling in a direction inclined at \[{{30}^{o}}\] to the horizontal after one more sec, it is travelling horizontally, the magnitude and direction of its velocity are [RPET 1999] (a) \[2\sqrt{20}\,m/\sec ,\,{{60}^{o}}\] (b) \[20\sqrt{3}\,m/\sec ,\,\,{{60}^{o}}\] (c) \[6\sqrt{40}\,\,m/\sec ,\,\,{{30}^{o}}\] (d) \[40\sqrt{6}\,m/\sec ,\,\,{{30}^{o}}\] Solution: (b) Let in 2 sec body reaches upto point A and after one more sec upto point B. 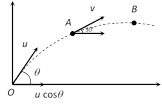 Total time of ascent for a body is given 3 sec i.e. \[t=\frac{u\sin \theta }{g}=3\] \[\therefore \,\,u\sin \theta =10\times 3=30\] ?.. (i) Horizontal component of velocity remains always constant \[u\cos \theta =v\cos 30{}^\circ \] ?.. (ii) For vertical upward motion between point O and A \[v\sin {{30}^{o}}=u\sin \theta -g\times 2\] \[\left[ \text{Using }v=u-g\,t \right]\] \[v\sin {{30}^{o}}=30-20\] \[\left[ \text{As}\,\,u\sin \text{ }\theta =\text{30} \right]\] \[\therefore \,\,v=20\,m/s.\] Substituting this value in equation (ii) \[u\cos \theta =20\,\cos {{30}^{o}}\]\[=10\sqrt{3}\] ?..(iii) From equation (i) and (iii) \[u=20\sqrt{3}\] and \[\theta =60{}^\circ \] Problem 12. A body is projected up a smooth inclined plane \[(length =20\sqrt{2}\,m)\] with velocity u from the point M as shown in the figure. The angle of inclination is \[4{{5}^{o}}\] and the top is connected to a well of diameter 40 m. If the body just manages to cross the well, what is the value of v (a) \[40\,m{{s}^{-1}}\] (b) \[40\sqrt{2}\,m{{s}^{-1}}\] (c) \[20\,m{{s}^{-1}}\] (d) \[20\sqrt{2}\,m{{s}^{-1}}\]
Total time of ascent for a body is given 3 sec i.e. \[t=\frac{u\sin \theta }{g}=3\] \[\therefore \,\,u\sin \theta =10\times 3=30\] ?.. (i) Horizontal component of velocity remains always constant \[u\cos \theta =v\cos 30{}^\circ \] ?.. (ii) For vertical upward motion between point O and A \[v\sin {{30}^{o}}=u\sin \theta -g\times 2\] \[\left[ \text{Using }v=u-g\,t \right]\] \[v\sin {{30}^{o}}=30-20\] \[\left[ \text{As}\,\,u\sin \text{ }\theta =\text{30} \right]\] \[\therefore \,\,v=20\,m/s.\] Substituting this value in equation (ii) \[u\cos \theta =20\,\cos {{30}^{o}}\]\[=10\sqrt{3}\] ?..(iii) From equation (i) and (iii) \[u=20\sqrt{3}\] and \[\theta =60{}^\circ \] Problem 12. A body is projected up a smooth inclined plane \[(length =20\sqrt{2}\,m)\] with velocity u from the point M as shown in the figure. The angle of inclination is \[4{{5}^{o}}\] and the top is connected to a well of diameter 40 m. If the body just manages to cross the well, what is the value of v (a) \[40\,m{{s}^{-1}}\] (b) \[40\sqrt{2}\,m{{s}^{-1}}\] (c) \[20\,m{{s}^{-1}}\] (d) \[20\sqrt{2}\,m{{s}^{-1}}\] 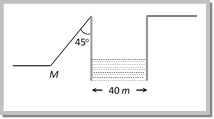 Solution: (d) At point N angle of projection of the body will be \[45{}^\circ \]. Let velocity of projection at this point is v. If the body just manages to cross the well then \[\text{Range}=\text{Diameter}\,\text{of}\,\text{well}\] \[\frac{{{v}^{2}}\sin 2\theta }{g}=40\] \[\left[ \text{As}\,\,\theta =\text{45}{}^\circ \right]\] \[{{v}^{2}}=400\] Þ \[v=20\,m/s\]
Solution: (d) At point N angle of projection of the body will be \[45{}^\circ \]. Let velocity of projection at this point is v. If the body just manages to cross the well then \[\text{Range}=\text{Diameter}\,\text{of}\,\text{well}\] \[\frac{{{v}^{2}}\sin 2\theta }{g}=40\] \[\left[ \text{As}\,\,\theta =\text{45}{}^\circ \right]\] \[{{v}^{2}}=400\] Þ \[v=20\,m/s\] 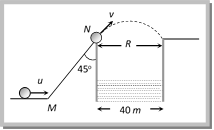 But we have to calculate the velocity (u) of the body at point M. For motion along the inclined plane (from M to N) Final velocity (v) = 20 m/s, acceleration (a) = ? g sina = ? g sin 45o, distance of inclined plane (s) = \[20\sqrt{2}\]m \[{{(20)}^{2}}={{u}^{2}}-2\frac{g}{\sqrt{2}}.20\sqrt{2}\] [Using \[{{\operatorname{v}}^{2}}= {{u}^{2}}+ 2as\]] \[{{u}^{2}}={{20}^{2}}+400\Rightarrow u=20\sqrt{2}\,m/s.\] Problem 13. A projectile is fired with velocity u making angle q with the horizontal. What is the change in velocity when it is at the highest point (a) \[u\text{ }cos\,\theta \] (b) u (c) \[u\text{ }sin\,\,\theta \] (d) \[(u\text{ }cos\,\theta \text{ }u)\] Solution: (c) Since horizontal component of velocity remain always constant therefore only vertical component of velocity changes. Initially vertical component \[u\sin \theta \] Finally it becomes zero. So change in velocity \[=u\sin \theta \]
But we have to calculate the velocity (u) of the body at point M. For motion along the inclined plane (from M to N) Final velocity (v) = 20 m/s, acceleration (a) = ? g sina = ? g sin 45o, distance of inclined plane (s) = \[20\sqrt{2}\]m \[{{(20)}^{2}}={{u}^{2}}-2\frac{g}{\sqrt{2}}.20\sqrt{2}\] [Using \[{{\operatorname{v}}^{2}}= {{u}^{2}}+ 2as\]] \[{{u}^{2}}={{20}^{2}}+400\Rightarrow u=20\sqrt{2}\,m/s.\] Problem 13. A projectile is fired with velocity u making angle q with the horizontal. What is the change in velocity when it is at the highest point (a) \[u\text{ }cos\,\theta \] (b) u (c) \[u\text{ }sin\,\,\theta \] (d) \[(u\text{ }cos\,\theta \text{ }u)\] Solution: (c) Since horizontal component of velocity remain always constant therefore only vertical component of velocity changes. Initially vertical component \[u\sin \theta \] Finally it becomes zero. So change in velocity \[=u\sin \theta \]
You need to login to perform this action.
You will be redirected in
3 sec
