Horizontal Range
Category : NEET
Horizontal Range Horizontal range: It is the horizontal distance travelled by a body during the time of flight. So by using second equation of motion 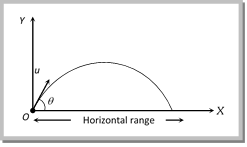 \[R=u\cos \theta \times T\]\[=\,\]\[u\cos \theta \times (2u\sin \theta /g)\]\[=\frac{{{u}^{2}}\,\sin \,2\theta }{g}\] \[R=\frac{{{u}^{2}}\,\sin \,2\theta }{g}\] (i) Range of projectile can also be expressed as: \[\operatorname{R} = u cos\,\theta \,\,\times \, T =u\cos \theta \frac{2u\sin \theta }{g}=\frac{2\,u\cos \theta \,\,u\sin \theta }{g}=\frac{\text{2}{{\text{u}}_{\text{x}}}{{u}_{y}}}{\text{g}}\] \ \[R=\frac{\text{2}{{\text{u}}_{\text{x}}}{{u}_{y}}}{\text{g}}\] (where \[{{\operatorname{u}}_{x}}\,and {{u}_{y}}\] are the horizontal and vertical component of initial velocity) (ii) If angle of projection is changed from \[\theta \] to \[\theta =(90\theta )\] then range remains unchanged.
\[R=u\cos \theta \times T\]\[=\,\]\[u\cos \theta \times (2u\sin \theta /g)\]\[=\frac{{{u}^{2}}\,\sin \,2\theta }{g}\] \[R=\frac{{{u}^{2}}\,\sin \,2\theta }{g}\] (i) Range of projectile can also be expressed as: \[\operatorname{R} = u cos\,\theta \,\,\times \, T =u\cos \theta \frac{2u\sin \theta }{g}=\frac{2\,u\cos \theta \,\,u\sin \theta }{g}=\frac{\text{2}{{\text{u}}_{\text{x}}}{{u}_{y}}}{\text{g}}\] \ \[R=\frac{\text{2}{{\text{u}}_{\text{x}}}{{u}_{y}}}{\text{g}}\] (where \[{{\operatorname{u}}_{x}}\,and {{u}_{y}}\] are the horizontal and vertical component of initial velocity) (ii) If angle of projection is changed from \[\theta \] to \[\theta =(90\theta )\] then range remains unchanged.  \[R'=\frac{{{u}^{2}}\sin 2\theta \,'\,}{g}=\frac{{{u}^{2}}\sin [2({{90}^{o}}-\theta )]}{g}=\frac{{{u}^{2}}\sin 2\theta \,}{g}=R\] So a projectile has same range at angles of projection q and (90 ? q), though time of flight, maximum height and trajectories are different. These angles q and \[{{90}^{o}}\theta \] are called complementary angles of projection and for complementary angles of projection ratio of range \[\frac{{{R}_{1}}}{{{R}_{2}}}=\frac{{{u}^{2}}\sin \,2\theta /g}{{{u}^{2}}\sin \,[2\,({{90}^{o}}-\theta )]\,/g}=1\Rightarrow \frac{{{R}_{1}}}{{{R}_{2}}}=1\] (iii) For angle of projection \[{{\theta }_{1}}= (45 \alpha )\] and \[{{\theta }_{2}}=(45\text{ }+\alpha )\], range will be same and equal to \[{{\operatorname{u}}^{2}}\,cos 2a/g.\] \[{{\theta }_{1}}\,and\,{{\theta }_{2}}\] are also the complementary angles.
\[R'=\frac{{{u}^{2}}\sin 2\theta \,'\,}{g}=\frac{{{u}^{2}}\sin [2({{90}^{o}}-\theta )]}{g}=\frac{{{u}^{2}}\sin 2\theta \,}{g}=R\] So a projectile has same range at angles of projection q and (90 ? q), though time of flight, maximum height and trajectories are different. These angles q and \[{{90}^{o}}\theta \] are called complementary angles of projection and for complementary angles of projection ratio of range \[\frac{{{R}_{1}}}{{{R}_{2}}}=\frac{{{u}^{2}}\sin \,2\theta /g}{{{u}^{2}}\sin \,[2\,({{90}^{o}}-\theta )]\,/g}=1\Rightarrow \frac{{{R}_{1}}}{{{R}_{2}}}=1\] (iii) For angle of projection \[{{\theta }_{1}}= (45 \alpha )\] and \[{{\theta }_{2}}=(45\text{ }+\alpha )\], range will be same and equal to \[{{\operatorname{u}}^{2}}\,cos 2a/g.\] \[{{\theta }_{1}}\,and\,{{\theta }_{2}}\] are also the complementary angles. 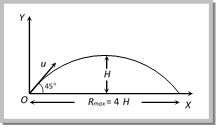 (iv) Maximum range: For range to be maximum \[\frac{dR}{d\theta }=0\]\[\Rightarrow \] \[\frac{d}{d\theta }\left[ \frac{{{u}^{2}}\,\sin \,2\theta }{g} \right]\,=\,0\] \[\Rightarrow cos 2\,\theta = 0\] i.e. \[2\theta =\text{ }{{90}^{o}}\,\Rightarrow ~\theta =\text{ }{{45}^{o}}~and~~{{R}_{max}}=\text{ }\left( {{u}^{2}}/g \right)\] i.e., a projectile will have maximum range when it is projected at an angle of 45o to the horizontal and the maximum range will be \[\left( {{u}^{2}}/g \right)\]. When the range is maximum, the height H reached by the projectile \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{{{u}^{2}}{{\sin }^{2}}45}{2g}=\frac{{{u}^{2}}}{4g}=\frac{{{R}_{\max }}}{4}\] i.e., if a person can throw a projectile to a maximum distance \[{{R}_{max}},\] The maximum height to which it will rise is \[\left( \frac{{{R}_{\max }}}{4} \right)\]. (v) Relation between horizontal range and maximum height: \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] and \[H=\,\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] \[\therefore \,\,\,\,\frac{R}{H}=\frac{{{u}^{2}}\sin 2\theta /g}{{{u}^{2}}{{\sin }^{2}}\theta /2g}=4\cot \theta \] \[\Rightarrow \,\,R=4H\cot \theta \] (vi) If in case of projectile motion range R is n times the maximum height H i.e. R = nH Þ \[\frac{{{u}^{2}}\sin 2\theta }{g}=n\,\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] Þ \[\tan \,\theta \,=[4/n]\] or \[\theta ={{\tan }^{-1}}[4/n]\] The angle of projection is given by \[\theta ={{\tan }^{-1}}[4/n]\] Note: q If R = H then \[\theta ={{\tan }^{-1}}(4)\] or \[\theta ={{76}^{o}}\]. If R = 4H then \[\theta ={{\tan }^{-1}}(1)\] or \[\theta ={{45}^{o}}\]. Sample problem based on horizontal range Problem 28. A boy playing on the roof of a 10m high building throws a ball with a speed of 10 m/s at an angle of \[{{30}^{o}}\] with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground (g = \[10\text{ }m/{{s}^{2}},\text{ }sin\text{ }{{30}^{o}}=\frac{1}{2}\], \[\cos \,{{30}^{o}}\,=\,\frac{\sqrt{3}}{2}\]) [AIEEE 2003] (a) 8.66 m (b) 5.20 m (c) 4.33 m (d) 2.60 m
(iv) Maximum range: For range to be maximum \[\frac{dR}{d\theta }=0\]\[\Rightarrow \] \[\frac{d}{d\theta }\left[ \frac{{{u}^{2}}\,\sin \,2\theta }{g} \right]\,=\,0\] \[\Rightarrow cos 2\,\theta = 0\] i.e. \[2\theta =\text{ }{{90}^{o}}\,\Rightarrow ~\theta =\text{ }{{45}^{o}}~and~~{{R}_{max}}=\text{ }\left( {{u}^{2}}/g \right)\] i.e., a projectile will have maximum range when it is projected at an angle of 45o to the horizontal and the maximum range will be \[\left( {{u}^{2}}/g \right)\]. When the range is maximum, the height H reached by the projectile \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{{{u}^{2}}{{\sin }^{2}}45}{2g}=\frac{{{u}^{2}}}{4g}=\frac{{{R}_{\max }}}{4}\] i.e., if a person can throw a projectile to a maximum distance \[{{R}_{max}},\] The maximum height to which it will rise is \[\left( \frac{{{R}_{\max }}}{4} \right)\]. (v) Relation between horizontal range and maximum height: \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] and \[H=\,\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] \[\therefore \,\,\,\,\frac{R}{H}=\frac{{{u}^{2}}\sin 2\theta /g}{{{u}^{2}}{{\sin }^{2}}\theta /2g}=4\cot \theta \] \[\Rightarrow \,\,R=4H\cot \theta \] (vi) If in case of projectile motion range R is n times the maximum height H i.e. R = nH Þ \[\frac{{{u}^{2}}\sin 2\theta }{g}=n\,\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] Þ \[\tan \,\theta \,=[4/n]\] or \[\theta ={{\tan }^{-1}}[4/n]\] The angle of projection is given by \[\theta ={{\tan }^{-1}}[4/n]\] Note: q If R = H then \[\theta ={{\tan }^{-1}}(4)\] or \[\theta ={{76}^{o}}\]. If R = 4H then \[\theta ={{\tan }^{-1}}(1)\] or \[\theta ={{45}^{o}}\]. Sample problem based on horizontal range Problem 28. A boy playing on the roof of a 10m high building throws a ball with a speed of 10 m/s at an angle of \[{{30}^{o}}\] with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground (g = \[10\text{ }m/{{s}^{2}},\text{ }sin\text{ }{{30}^{o}}=\frac{1}{2}\], \[\cos \,{{30}^{o}}\,=\,\frac{\sqrt{3}}{2}\]) [AIEEE 2003] (a) 8.66 m (b) 5.20 m (c) 4.33 m (d) 2.60 m 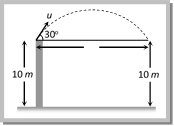 Solution: (a) Simply we have to calculate the range of projectile \[R=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{(10)}^{2}}\sin (2\times 30{}^\circ )}{10}\] \[R=5\sqrt{3}=8.66\,\,meter\] Problem 29. Which of the following sets of factors will affect the horizontal distance covered by an athlete in a long?jump event [AMU (Engg.) 2001] (a) Speed before he jumps and his weight (b) The direction in which he leaps and the initial speed (c) The force with which he pushes the ground and his speed (d) The direction in which he leaps and the weight Solution: (b) Because range \[=\frac{{{(\text{Velocity of}\,\text{projection)}}^{\text{2}}}\,\times \sin \,2(\text{Angle of projection)}}{g}\] Problem 30. For a projectile, the ratio of maximum height reached to the square of flight time is \[\left( g = 10 m{{s}^{2}} \right)\] [EAMCET (Med.) 2000] (a) 5 : 4 (b) 5 : 2 (c) 5 : 1 (d) 10 : 1 Solution: (a) \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] and \[T=\frac{2u\sin \theta }{g}\] \[\therefore \,\,\frac{H}{{{T}^{2}}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta /2g}{4\,{{u}^{2}}{{\sin }^{2}}\theta /{{g}^{2}}}=\frac{g}{8}=\frac{10}{8}=\frac{5}{4}\] Problem 31. A cricketer can throw a ball to a maximum horizontal distance of 100 m. The speed with which he throws the ball is (to the nearest integer) [Kerala (Med.) 2002] (a) \[30 m{{s}^{1}}\] (b) \[42\text{ }m{{s}^{1}}\] (c) \[32\text{ }m{{s}^{1}}\] (d) \[35\text{ }m{{s}^{1}}\] Solution: (c) \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=\text{ }100\] (when \[\theta =45{}^\circ \]) \[\therefore \,\,\,u=\sqrt{1000}\,\,\,=31.62\,m/s.\] Problem 32. If two bodies are projected at 30o and 60o respectively, with the same velocity, then [CBSE PMT 2000; JIPMER 2002] (a) Their ranges are same (b) Their heights are same (c) Their times of flight are same (d) All of these Solution: (a) Because these are complementary angles. Problem 33. Figure shows four paths for a kicked football. Ignoring the effects of air on the flight, rank the paths according to initial horizontal velocity component, highest first [AMU (Med.) 2000]
Solution: (a) Simply we have to calculate the range of projectile \[R=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{(10)}^{2}}\sin (2\times 30{}^\circ )}{10}\] \[R=5\sqrt{3}=8.66\,\,meter\] Problem 29. Which of the following sets of factors will affect the horizontal distance covered by an athlete in a long?jump event [AMU (Engg.) 2001] (a) Speed before he jumps and his weight (b) The direction in which he leaps and the initial speed (c) The force with which he pushes the ground and his speed (d) The direction in which he leaps and the weight Solution: (b) Because range \[=\frac{{{(\text{Velocity of}\,\text{projection)}}^{\text{2}}}\,\times \sin \,2(\text{Angle of projection)}}{g}\] Problem 30. For a projectile, the ratio of maximum height reached to the square of flight time is \[\left( g = 10 m{{s}^{2}} \right)\] [EAMCET (Med.) 2000] (a) 5 : 4 (b) 5 : 2 (c) 5 : 1 (d) 10 : 1 Solution: (a) \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] and \[T=\frac{2u\sin \theta }{g}\] \[\therefore \,\,\frac{H}{{{T}^{2}}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta /2g}{4\,{{u}^{2}}{{\sin }^{2}}\theta /{{g}^{2}}}=\frac{g}{8}=\frac{10}{8}=\frac{5}{4}\] Problem 31. A cricketer can throw a ball to a maximum horizontal distance of 100 m. The speed with which he throws the ball is (to the nearest integer) [Kerala (Med.) 2002] (a) \[30 m{{s}^{1}}\] (b) \[42\text{ }m{{s}^{1}}\] (c) \[32\text{ }m{{s}^{1}}\] (d) \[35\text{ }m{{s}^{1}}\] Solution: (c) \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=\text{ }100\] (when \[\theta =45{}^\circ \]) \[\therefore \,\,\,u=\sqrt{1000}\,\,\,=31.62\,m/s.\] Problem 32. If two bodies are projected at 30o and 60o respectively, with the same velocity, then [CBSE PMT 2000; JIPMER 2002] (a) Their ranges are same (b) Their heights are same (c) Their times of flight are same (d) All of these Solution: (a) Because these are complementary angles. Problem 33. Figure shows four paths for a kicked football. Ignoring the effects of air on the flight, rank the paths according to initial horizontal velocity component, highest first [AMU (Med.) 2000] 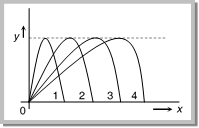 (a) 1, 2, 3, 4 (b) 2, 3, 4, 1 (c) 3, 4, 1, 2 (d) 4, 3, 2, 1 Solution: (d) Range\[\propto \]horizontal component of velocity. Graph 4 shows maximum range, so football possess maximum horizontal velocity in this case. Problem 34. Four bodies P, Q, R and S are projected with equal velocities having angles of projection 15o, 30o, 45o and 60o with the horizontal respectively. The body having shortest range is [EAMCET (Engg.) 2000] (a) P (b) Q (c) R (d) S Solution: (a) Range of projectile will be minimum for that angle which is farthest from \[45{}^\circ \]. Problem 35. A particle covers 50 m distance when projected with an initial speed. On the same surface it will cover a distance, when projected with double the initial speed [RPMT 2000] (a) 100 m (b) 150 m (c) 200 m (d) 250 m Solution: (c) \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] \[\therefore \,\,R\propto {{u}^{2}}\] so \[\frac{{{R}_{2}}}{{{R}_{1}}}={{\left( \frac{{{u}_{2}}}{{{u}_{1}}} \right)}^{2}}\]\[={{\left( \frac{2u}{u} \right)}^{2}}\] \[\Rightarrow {{R}_{2}}=4{{R}_{1}}\]\[= 4\,\,\times \,\,50 = 200 m\] Problem 36. A bullet is fired from a canon with velocity 500 m/s. If the angle of projection is 15o and g = 10 m/s2. Then the range is [CPMT 1997] (a) \[25 \times 1{{0}^{3}}m\] (b) \[12.5 \times 1{{0}^{3}}m\] (c) \[50 \times 1{{0}^{2}}m\] (d) \[25 \times 1{{0}^{2}}m\] Solution: (b) \[Range\,(R)=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{\left( 500 \right)}^{2}}\sin \left( 2\times 15 \right)}{10}=12500\,m\,=12.5\times {{10}^{3}}\,m\] Problem 37. A projectile thrown with a speed v at an angle q has a range R on the surface of earth. For same v and q, its range on the surface of moon will be (a) R/6 (b) 6 R (c) R/36 (d) 36 R Solution : (b) \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] \[\therefore \,\,R\propto 1/g\] \[\frac{{{R}_{Moon}}}{{{R}_{Earth}}}=\frac{{{g}_{Earth}}}{{{g}_{Moon}}}=6\,\,\,\,\,\,\,\,\,\left[ \because \,\,{{g}_{Moon}}=\frac{1}{6}\,{{g}_{Earth}} \right]\] \[\therefore \,{{R}_{Moon}}=6\,{{R}_{Earth}}=6R\] Problem 38. A projectile is thrown into space so as to have maximum horizontal range R. Taking the point of projection as origin, the co-ordinates of the point where the speed of the particle is minimum are (a) (R, R) (b) \[\left( R,\,\frac{R}{2} \right)\] (c) \[\left( \frac{R}{2},\,\frac{R}{4} \right)\] (d) \[\left( R,\,\frac{R}{4} \right)\] Solution : (c) For maximum horizontal Range \[\theta =45{}^\circ \] From \[R=4H\cot \theta \]= 4H [As q = 45o, for maximum range.] Speed of the particle will be minimum at the highest point of parabola. So the co-ordinate of the highest point will be (R/2, R/4)
(a) 1, 2, 3, 4 (b) 2, 3, 4, 1 (c) 3, 4, 1, 2 (d) 4, 3, 2, 1 Solution: (d) Range\[\propto \]horizontal component of velocity. Graph 4 shows maximum range, so football possess maximum horizontal velocity in this case. Problem 34. Four bodies P, Q, R and S are projected with equal velocities having angles of projection 15o, 30o, 45o and 60o with the horizontal respectively. The body having shortest range is [EAMCET (Engg.) 2000] (a) P (b) Q (c) R (d) S Solution: (a) Range of projectile will be minimum for that angle which is farthest from \[45{}^\circ \]. Problem 35. A particle covers 50 m distance when projected with an initial speed. On the same surface it will cover a distance, when projected with double the initial speed [RPMT 2000] (a) 100 m (b) 150 m (c) 200 m (d) 250 m Solution: (c) \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] \[\therefore \,\,R\propto {{u}^{2}}\] so \[\frac{{{R}_{2}}}{{{R}_{1}}}={{\left( \frac{{{u}_{2}}}{{{u}_{1}}} \right)}^{2}}\]\[={{\left( \frac{2u}{u} \right)}^{2}}\] \[\Rightarrow {{R}_{2}}=4{{R}_{1}}\]\[= 4\,\,\times \,\,50 = 200 m\] Problem 36. A bullet is fired from a canon with velocity 500 m/s. If the angle of projection is 15o and g = 10 m/s2. Then the range is [CPMT 1997] (a) \[25 \times 1{{0}^{3}}m\] (b) \[12.5 \times 1{{0}^{3}}m\] (c) \[50 \times 1{{0}^{2}}m\] (d) \[25 \times 1{{0}^{2}}m\] Solution: (b) \[Range\,(R)=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{\left( 500 \right)}^{2}}\sin \left( 2\times 15 \right)}{10}=12500\,m\,=12.5\times {{10}^{3}}\,m\] Problem 37. A projectile thrown with a speed v at an angle q has a range R on the surface of earth. For same v and q, its range on the surface of moon will be (a) R/6 (b) 6 R (c) R/36 (d) 36 R Solution : (b) \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] \[\therefore \,\,R\propto 1/g\] \[\frac{{{R}_{Moon}}}{{{R}_{Earth}}}=\frac{{{g}_{Earth}}}{{{g}_{Moon}}}=6\,\,\,\,\,\,\,\,\,\left[ \because \,\,{{g}_{Moon}}=\frac{1}{6}\,{{g}_{Earth}} \right]\] \[\therefore \,{{R}_{Moon}}=6\,{{R}_{Earth}}=6R\] Problem 38. A projectile is thrown into space so as to have maximum horizontal range R. Taking the point of projection as origin, the co-ordinates of the point where the speed of the particle is minimum are (a) (R, R) (b) \[\left( R,\,\frac{R}{2} \right)\] (c) \[\left( \frac{R}{2},\,\frac{R}{4} \right)\] (d) \[\left( R,\,\frac{R}{4} \right)\] Solution : (c) For maximum horizontal Range \[\theta =45{}^\circ \] From \[R=4H\cot \theta \]= 4H [As q = 45o, for maximum range.] Speed of the particle will be minimum at the highest point of parabola. So the co-ordinate of the highest point will be (R/2, R/4) 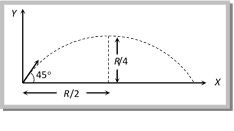 Problem 39. The speed of a projectile at the highest point becomes \[\frac{1}{\sqrt{2}}\] times its initial speed. The horizontal range of the projectile will be (a) \[\frac{{{u}^{2}}}{g}\] (b) \[\frac{{{u}^{2}}}{2g}\] (c) \[\frac{{{u}^{2}}}{3g}\] (d) \[\frac{{{u}^{2}}}{4g}\] Solution: (a) Velocity at the highest point is given by \[u\cos \theta =\frac{u}{\sqrt{2}}\] (given) \[\therefore \,\,\theta ={{45}^{o}}~\] Horizontal range \[R=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{u}^{2}}\sin (2\times {{45}^{o}})}{g}=\frac{{{u}^{2}}}{g}\] Problem 40. A large number of bullets are fired in all directions with same speed u. What is the maximum area on the ground on which these bullets will spread (a) \[\pi \frac{{{u}^{2}}}{g}\] (b) \[\pi \frac{{{u}^{4}}}{{{g}^{2}}}\] (c) \[{{\pi }^{2}}\frac{{{u}^{4}}}{{{g}^{2}}}\] (d) \[{{\pi }^{2}}\frac{{{u}^{2}}}{{{g}^{2}}}\] Solution: (b) The maximum area will be equal to area of the circle with radius equal to the maximum range of projectile Maximum area \[\pi {{r}^{2}}=\pi {{\left( {{R}_{\max }} \right)}^{2}}\] \[=\pi {{\left( \frac{{{u}^{2}}}{g} \right)}^{2}}\]\[=\pi \frac{{{u}^{4}}}{{{g}^{2}}}\] [As \[r={{R}_{\max }}={{u}^{2}}/g\,\] for \[\theta = 4{{5}^{o}}\]] Problem 41. A projectile is projected with initial velocity \[(6\hat{i}+8\hat{j})\,m/sec.\] If g = 10 ms?2, then horizontal range is (a) 4.8 metre (b) 9.6 metre (c) 19.2 metre (d) 14.0 metre Solution: (b) Initial velocity \[=\left( 6\hat{i}+8\hat{J} \right)\,m/s\] (given) Magnitude of velocity of projection \[\operatorname{u}=\sqrt{u_{x}^{2}+u_{y}^{2}}=\sqrt{{{6}^{2}}+{{8}^{2}}}= 10 m/s\] Angle of projection \[\tan \theta =\frac{{{u}_{y}}}{{{u}_{x}}}=\frac{8}{6}=\frac{4}{3}\,\,\,\,\therefore \,\,\sin \theta =\frac{4}{5}\] and \[\cos \theta =\frac{3}{5}\] Now horizontal range \[R=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{u}^{2}}2\sin \theta \cos \theta }{g}=\frac{{{(10)}^{2}}\times \,2\times \,\frac{4}{5}\times \,\frac{3}{5}}{10}=9.6\,\,meter\] Problem 42. A projectile thrown with an initial speed u and angle of projection 15o to the horizontal has a range R. If the same projectile is thrown at an angle of 45o to the horizontal with speed 2u, its range will be (a) 12 R (b) 3 R (c) 8 R (d) 4 R Solution: (c) \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] \[\therefore \,\,R\propto {{u}^{2}}\sin 2\theta \] \[\frac{{{R}_{2}}}{{{R}_{1}}}={{\left( \frac{{{u}_{2}}}{{{u}_{1}}} \right)}^{2}}\,\,\left( \frac{\sin \,2{{\theta }_{2}}}{\sin \,2{{\theta }_{1}}} \right)\Rightarrow {{R}_{2}}={{R}_{1}}\,{{\left( \frac{2u}{u} \right)}^{2}}\left( \frac{\sin {{90}^{o}}}{\sin {{30}^{o}}} \right)=8{{R}_{1}}\] Problem 43. The velocity at the maximum height of a projectile is half of its initial velocity of projection u. Its range on the horizontal plane is [MP PET 1993] (a) \[\sqrt{3}{{u}^{2}}/2g\] (b) \[{{u}^{2}}/3g\] (c) \[3{{u}^{2}}/2g\] (d) \[3{{u}^{2}}/g\] Solution: (a) If the velocity of projection is u then at the highest point body posses only \[u\cos \theta \] \[u\cos \theta =\frac{u}{2}\] (given) \[\therefore \,\,\theta =60{}^\circ \] Now \[R=\frac{{{u}^{2}}\sin (2\times 60{}^\circ )}{g}=\frac{\sqrt{3}}{2}\frac{{{u}^{2}}}{g}\] Problem 44. A projectile is thrown from a point in a horizontal place such that its horizontal and vertical velocity component are 9.8 m/s and 19.6 m/s respectively. Its horizontal range is (a) 4.9 m (b) 9.8 m (c) 19.6 m (d) 39.2 m Solution: (d) We know \[R=\frac{2{{u}_{x}}\,{{u}_{y}}}{g}=\frac{2\times 9.8\times 19.6}{9.8}=39.2\,m\] Where \[{{u}_{x}}=\] horizontal component of initial velocity, \[{{u}_{y}}=\] vertical component of initial velocity. Problem 45. A particle is projected with a velocity v such that its range on the horizontal plane is twice the greatest height attained by it. The range of the projectile is (where g is acceleration due to gravity) [BHU 1984] (a) \[\frac{4{{v}^{2}}}{5g}\] (b) \[\frac{4g}{5{{v}^{2}}}\] (c) \[\frac{{{v}^{2}}}{g}\] (d) \[{{F}_{A}},\ {{F}_{B}}\] Solution: (a) We know \[R=4H\cot \theta \] \[2H=4H\cot \theta \,\,\Rightarrow \,\cot \theta =\frac{1}{2};\,\,\sin \theta =\frac{2}{\sqrt{5}};\,\,\,\cos \theta =\frac{1}{\sqrt{5}}\] \[\left[ \text{As }R=2H\text{ given} \right]\] \[\text{Range}=\frac{{{u}^{2}}\,.\,2.\,\sin \theta \,.\,\cos \theta }{g}=\frac{2{{u}^{2}}\frac{2}{\sqrt{5}}\,.\,\frac{1}{\sqrt{5}}}{g}=\frac{4{{u}^{2}}}{5g}\] Problem 46. The range R of projectile is same when its maximum heights are h1 and h2. What is the relation between R and \[{{\operatorname{h}}_{1}}\,and {{h}_{2}}\] [EAMCET (Med.) 2000] (a) \[R=\sqrt{{{h}_{1}}{{h}_{2}}}\] (b) \[R=\sqrt{2{{h}_{1}}{{h}_{2}}}\] (c) \[R=2\sqrt{{{h}_{1}}{{h}_{2}}}\] (d) \[R=4\sqrt{{{h}_{1}}{{h}_{2}}}\] Solution: (d) For equal ranges body should be projected with angle \[\theta \] or \[({{90}^{o}}-\theta )\] from the horizontal. And for these angles: \[{{h}_{1}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] and \[{{h}_{2}}=\frac{{{u}^{2}}{{\cos }^{2}}\theta }{2g}\] by multiplication of both height: \[{{h}_{1}}\,{{h}_{2}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta \,{{\cos }^{2}}\theta }{4{{g}^{2}}}\]\[=\frac{1}{16}{{\left( \frac{{{u}^{2}}\sin 2\,\theta }{g} \right)}^{2}}\] \[\Rightarrow 16{{h}_{1\,}}{{h}_{2}}={{R}^{2}}\Rightarrow R=4\sqrt{{{h}_{1}}{{h}_{2}}}\] Problem 47. A grasshopper can jump maximum distance 1.6 m. It spends negligible time on the ground. How far can it go in 10 seconds (a) \[5\sqrt{2}\,m\] (b) \[10\sqrt{2}\,m\] (c) \[20\sqrt{2}\,m\] (d) \[40\sqrt{2}\,m\]
Problem 39. The speed of a projectile at the highest point becomes \[\frac{1}{\sqrt{2}}\] times its initial speed. The horizontal range of the projectile will be (a) \[\frac{{{u}^{2}}}{g}\] (b) \[\frac{{{u}^{2}}}{2g}\] (c) \[\frac{{{u}^{2}}}{3g}\] (d) \[\frac{{{u}^{2}}}{4g}\] Solution: (a) Velocity at the highest point is given by \[u\cos \theta =\frac{u}{\sqrt{2}}\] (given) \[\therefore \,\,\theta ={{45}^{o}}~\] Horizontal range \[R=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{u}^{2}}\sin (2\times {{45}^{o}})}{g}=\frac{{{u}^{2}}}{g}\] Problem 40. A large number of bullets are fired in all directions with same speed u. What is the maximum area on the ground on which these bullets will spread (a) \[\pi \frac{{{u}^{2}}}{g}\] (b) \[\pi \frac{{{u}^{4}}}{{{g}^{2}}}\] (c) \[{{\pi }^{2}}\frac{{{u}^{4}}}{{{g}^{2}}}\] (d) \[{{\pi }^{2}}\frac{{{u}^{2}}}{{{g}^{2}}}\] Solution: (b) The maximum area will be equal to area of the circle with radius equal to the maximum range of projectile Maximum area \[\pi {{r}^{2}}=\pi {{\left( {{R}_{\max }} \right)}^{2}}\] \[=\pi {{\left( \frac{{{u}^{2}}}{g} \right)}^{2}}\]\[=\pi \frac{{{u}^{4}}}{{{g}^{2}}}\] [As \[r={{R}_{\max }}={{u}^{2}}/g\,\] for \[\theta = 4{{5}^{o}}\]] Problem 41. A projectile is projected with initial velocity \[(6\hat{i}+8\hat{j})\,m/sec.\] If g = 10 ms?2, then horizontal range is (a) 4.8 metre (b) 9.6 metre (c) 19.2 metre (d) 14.0 metre Solution: (b) Initial velocity \[=\left( 6\hat{i}+8\hat{J} \right)\,m/s\] (given) Magnitude of velocity of projection \[\operatorname{u}=\sqrt{u_{x}^{2}+u_{y}^{2}}=\sqrt{{{6}^{2}}+{{8}^{2}}}= 10 m/s\] Angle of projection \[\tan \theta =\frac{{{u}_{y}}}{{{u}_{x}}}=\frac{8}{6}=\frac{4}{3}\,\,\,\,\therefore \,\,\sin \theta =\frac{4}{5}\] and \[\cos \theta =\frac{3}{5}\] Now horizontal range \[R=\frac{{{u}^{2}}\sin 2\theta }{g}=\frac{{{u}^{2}}2\sin \theta \cos \theta }{g}=\frac{{{(10)}^{2}}\times \,2\times \,\frac{4}{5}\times \,\frac{3}{5}}{10}=9.6\,\,meter\] Problem 42. A projectile thrown with an initial speed u and angle of projection 15o to the horizontal has a range R. If the same projectile is thrown at an angle of 45o to the horizontal with speed 2u, its range will be (a) 12 R (b) 3 R (c) 8 R (d) 4 R Solution: (c) \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] \[\therefore \,\,R\propto {{u}^{2}}\sin 2\theta \] \[\frac{{{R}_{2}}}{{{R}_{1}}}={{\left( \frac{{{u}_{2}}}{{{u}_{1}}} \right)}^{2}}\,\,\left( \frac{\sin \,2{{\theta }_{2}}}{\sin \,2{{\theta }_{1}}} \right)\Rightarrow {{R}_{2}}={{R}_{1}}\,{{\left( \frac{2u}{u} \right)}^{2}}\left( \frac{\sin {{90}^{o}}}{\sin {{30}^{o}}} \right)=8{{R}_{1}}\] Problem 43. The velocity at the maximum height of a projectile is half of its initial velocity of projection u. Its range on the horizontal plane is [MP PET 1993] (a) \[\sqrt{3}{{u}^{2}}/2g\] (b) \[{{u}^{2}}/3g\] (c) \[3{{u}^{2}}/2g\] (d) \[3{{u}^{2}}/g\] Solution: (a) If the velocity of projection is u then at the highest point body posses only \[u\cos \theta \] \[u\cos \theta =\frac{u}{2}\] (given) \[\therefore \,\,\theta =60{}^\circ \] Now \[R=\frac{{{u}^{2}}\sin (2\times 60{}^\circ )}{g}=\frac{\sqrt{3}}{2}\frac{{{u}^{2}}}{g}\] Problem 44. A projectile is thrown from a point in a horizontal place such that its horizontal and vertical velocity component are 9.8 m/s and 19.6 m/s respectively. Its horizontal range is (a) 4.9 m (b) 9.8 m (c) 19.6 m (d) 39.2 m Solution: (d) We know \[R=\frac{2{{u}_{x}}\,{{u}_{y}}}{g}=\frac{2\times 9.8\times 19.6}{9.8}=39.2\,m\] Where \[{{u}_{x}}=\] horizontal component of initial velocity, \[{{u}_{y}}=\] vertical component of initial velocity. Problem 45. A particle is projected with a velocity v such that its range on the horizontal plane is twice the greatest height attained by it. The range of the projectile is (where g is acceleration due to gravity) [BHU 1984] (a) \[\frac{4{{v}^{2}}}{5g}\] (b) \[\frac{4g}{5{{v}^{2}}}\] (c) \[\frac{{{v}^{2}}}{g}\] (d) \[{{F}_{A}},\ {{F}_{B}}\] Solution: (a) We know \[R=4H\cot \theta \] \[2H=4H\cot \theta \,\,\Rightarrow \,\cot \theta =\frac{1}{2};\,\,\sin \theta =\frac{2}{\sqrt{5}};\,\,\,\cos \theta =\frac{1}{\sqrt{5}}\] \[\left[ \text{As }R=2H\text{ given} \right]\] \[\text{Range}=\frac{{{u}^{2}}\,.\,2.\,\sin \theta \,.\,\cos \theta }{g}=\frac{2{{u}^{2}}\frac{2}{\sqrt{5}}\,.\,\frac{1}{\sqrt{5}}}{g}=\frac{4{{u}^{2}}}{5g}\] Problem 46. The range R of projectile is same when its maximum heights are h1 and h2. What is the relation between R and \[{{\operatorname{h}}_{1}}\,and {{h}_{2}}\] [EAMCET (Med.) 2000] (a) \[R=\sqrt{{{h}_{1}}{{h}_{2}}}\] (b) \[R=\sqrt{2{{h}_{1}}{{h}_{2}}}\] (c) \[R=2\sqrt{{{h}_{1}}{{h}_{2}}}\] (d) \[R=4\sqrt{{{h}_{1}}{{h}_{2}}}\] Solution: (d) For equal ranges body should be projected with angle \[\theta \] or \[({{90}^{o}}-\theta )\] from the horizontal. And for these angles: \[{{h}_{1}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] and \[{{h}_{2}}=\frac{{{u}^{2}}{{\cos }^{2}}\theta }{2g}\] by multiplication of both height: \[{{h}_{1}}\,{{h}_{2}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta \,{{\cos }^{2}}\theta }{4{{g}^{2}}}\]\[=\frac{1}{16}{{\left( \frac{{{u}^{2}}\sin 2\,\theta }{g} \right)}^{2}}\] \[\Rightarrow 16{{h}_{1\,}}{{h}_{2}}={{R}^{2}}\Rightarrow R=4\sqrt{{{h}_{1}}{{h}_{2}}}\] Problem 47. A grasshopper can jump maximum distance 1.6 m. It spends negligible time on the ground. How far can it go in 10 seconds (a) \[5\sqrt{2}\,m\] (b) \[10\sqrt{2}\,m\] (c) \[20\sqrt{2}\,m\] (d) \[40\sqrt{2}\,m\] 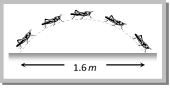 Solution: (c) Horizontal distance travelled by grasshopper will be maximum for \[\theta =45{}^\circ \] \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=1.6\,m\Rightarrow \,u=4\,m/s.\] Horizontal component of velocity of grasshopper \[u\cos \theta =4\cos 45=2\sqrt{2\,}\,m/s\] Total distance covered by it in 10 sec. \[S=u\,\,\cos \theta \times t=2\sqrt{2}\times 10\,\,\,=20\sqrt{2}\,m\] Problem 48. A projectile is thrown with an initial velocity of \[v=a\hat{i}+b\hat{j},\] if the range of projectile is double the maximum height reached by it then (a) a = 2b (b) b = a (c) b = 2a (d) b = 4a Solution: (c) Angle of projection \[\theta ={{\tan }^{-1}}\frac{{{v}_{y}}}{{{v}_{x}}}={{\tan }^{-1}}\frac{b}{a}\] \[\therefore \,\,\,\tan \theta =\frac{b}{a}\] ? (i) From formula \[R=4H\cot \theta =2H\Rightarrow \cot \theta =\frac{1}{2}\] \[\therefore \,\,\,\tan \theta =2\] ? (ii) [As \[R\text{ }=\text{ }2H\] given] From equation (i) and (ii) \[\operatorname{b} = 2a\]
Solution: (c) Horizontal distance travelled by grasshopper will be maximum for \[\theta =45{}^\circ \] \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=1.6\,m\Rightarrow \,u=4\,m/s.\] Horizontal component of velocity of grasshopper \[u\cos \theta =4\cos 45=2\sqrt{2\,}\,m/s\] Total distance covered by it in 10 sec. \[S=u\,\,\cos \theta \times t=2\sqrt{2}\times 10\,\,\,=20\sqrt{2}\,m\] Problem 48. A projectile is thrown with an initial velocity of \[v=a\hat{i}+b\hat{j},\] if the range of projectile is double the maximum height reached by it then (a) a = 2b (b) b = a (c) b = 2a (d) b = 4a Solution: (c) Angle of projection \[\theta ={{\tan }^{-1}}\frac{{{v}_{y}}}{{{v}_{x}}}={{\tan }^{-1}}\frac{b}{a}\] \[\therefore \,\,\,\tan \theta =\frac{b}{a}\] ? (i) From formula \[R=4H\cot \theta =2H\Rightarrow \cot \theta =\frac{1}{2}\] \[\therefore \,\,\,\tan \theta =2\] ? (ii) [As \[R\text{ }=\text{ }2H\] given] From equation (i) and (ii) \[\operatorname{b} = 2a\]
You need to login to perform this action.
You will be redirected in
3 sec
